第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
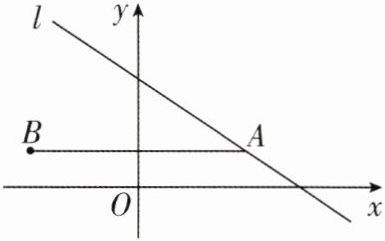
1 [2025陕西咸阳质检,中]如图,在平面直角坐标系中,直线l:$y= -\frac{2}{3}x+3$经过点A,点A的横坐标为3,点A与点B关于y轴对称.
(1)求点B的坐标;
(2)将直线l沿y轴向下平移得到直线$l'$,$l'$与y轴交于点C,若$\triangle ABC$的面积为3,求平移后的直线$l'$的函数表达式.
(1)求点B的坐标;
(2)将直线l沿y轴向下平移得到直线$l'$,$l'$与y轴交于点C,若$\triangle ABC$的面积为3,求平移后的直线$l'$的函数表达式.

答案:
【解】
(1)把x=3代入$y=-\dfrac{2}{3}x+3$,得$y=-\dfrac{2}{3}× 3+3=1$,所以点A(3,1).
因为点A与点B关于y轴对称,所以点B的坐标为(-3,1).
(2)由A(3,1),B(-3,1)可知AB=6.如图,
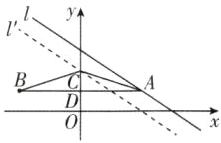
设AB与y轴的交点为D,则D(0,1).因为$S_{\triangle ABC}=3$,所以$\dfrac{1}{2}AB\cdot CD=3$,所以$\dfrac{1}{2}× 6CD=3$,所以CD=1.因为直线$l'$是由直线l沿y轴向下平移得到的,所以可设直线$l'$的函数表达式为$y=-\dfrac{2}{3}x+b$.
①当点C在AB上方时,点C的坐标为(0,2),将(0,2)代入$y=-\dfrac{2}{3}x+b$,得b=2,所以直线$l'$的函数表达式为$y=-\dfrac{2}{3}x+2$.
②当点C在AB下方时,点C的坐标为(0,0),将(0,0)代入$y=-\dfrac{2}{3}x+b$,得b=0,所以直线$l'$的函数表达式为$y=-\dfrac{2}{3}x$.
综上,平移后的直线$l'$的函数表达式为$y=-\dfrac{2}{3}x+2$或$y=-\dfrac{2}{3}x$.
【解】
(1)把x=3代入$y=-\dfrac{2}{3}x+3$,得$y=-\dfrac{2}{3}× 3+3=1$,所以点A(3,1).
因为点A与点B关于y轴对称,所以点B的坐标为(-3,1).
(2)由A(3,1),B(-3,1)可知AB=6.如图,

设AB与y轴的交点为D,则D(0,1).因为$S_{\triangle ABC}=3$,所以$\dfrac{1}{2}AB\cdot CD=3$,所以$\dfrac{1}{2}× 6CD=3$,所以CD=1.因为直线$l'$是由直线l沿y轴向下平移得到的,所以可设直线$l'$的函数表达式为$y=-\dfrac{2}{3}x+b$.
①当点C在AB上方时,点C的坐标为(0,2),将(0,2)代入$y=-\dfrac{2}{3}x+b$,得b=2,所以直线$l'$的函数表达式为$y=-\dfrac{2}{3}x+2$.
②当点C在AB下方时,点C的坐标为(0,0),将(0,0)代入$y=-\dfrac{2}{3}x+b$,得b=0,所以直线$l'$的函数表达式为$y=-\dfrac{2}{3}x$.
综上,平移后的直线$l'$的函数表达式为$y=-\dfrac{2}{3}x+2$或$y=-\dfrac{2}{3}x$.
2 [2024江苏盐城调研,中]如图,在平面直角坐标系中,一次函数$y= 2x-1$的图象分别交x轴、y轴于点A,B,将直线AB绕点B按顺时针方向旋转$45^{\circ}$,交x轴于点C,则直线BC的函数表达式是______.


答案:
$y=\dfrac{1}{3}x-1$
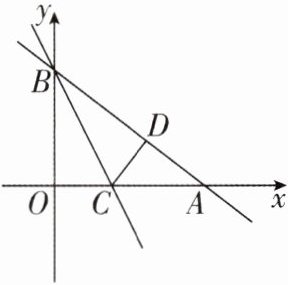
3 [较难]如图,某个一次函数的图象与x轴、y轴分别交于A,B两点,且A,B两点的坐标分别为$(4,0)$,$(0,3)$.
(1)求该一次函数的表达式.
(2)点C在线段OA上,沿直线BC将$\triangle OBC$翻折,O点恰好落在AB上的D点处,求直线BC的表达式.
(3)x轴上是否存在点P,使$\triangle ABP$为等腰三角形?若存在,请直接写出P点坐标;若不存在,请说明理由.
(1)求该一次函数的表达式.
(2)点C在线段OA上,沿直线BC将$\triangle OBC$翻折,O点恰好落在AB上的D点处,求直线BC的表达式.
(3)x轴上是否存在点P,使$\triangle ABP$为等腰三角形?若存在,请直接写出P点坐标;若不存在,请说明理由.

答案:
【解】
(1)设该一次函数的表达式为$y=kx+b(k\neq 0)$.将B点坐标(0,3)代入得b=3,再将A点坐标(4,0)代入$y=kx+3$,解得$k=-\dfrac{3}{4}$,所以$y=-\dfrac{3}{4}x+3$.
(2)由题意得OA=4,OB=3,所以AB=5.由翻折可得OC=CD,BD=BO=3,所以AD=2.设CD=OC=x,则AC=OA-OC=4-x.在$Rt\triangle ACD$中,由勾股定理得$CD^2+AD^2=AC^2$,即$x^2+2^2=(4-x)^2$,解得$x=\dfrac{3}{2}$,所以C的坐标为$\left( \dfrac{3}{2},0\right)$.设直线BC的表达式为$y=mx+n(m\neq 0)$.将B点坐标(0,3)代入得n=3,再将C点坐标$\left( \dfrac{3}{2},0\right)$代入$y=mx+3$,解得m=-2,所以直线BC的表达式为$y=-2x+3$.
(3)存在.P点坐标为(-4,0)或(-1,0)或(9,0)或$\left( \dfrac{7}{8},0\right)$.

如图,当$AB=P_1B$时,因为AO=4,所以$OP_1=AO=4$,所以$P_1(-4,0)$.当$AB=AP_2$时,$OP_2=AB-AO=1$,所以$P_2(-1,0)$.当$P_3A=P_3B$时,设$OP_3=x$,则$BP_3=4-x$,所以$3^2+x^2=(4-x)^2$,解得$x=\dfrac{7}{8}$,所以$P_3\left( \dfrac{7}{8},0\right)$.当$AB=AP_4$时,$AP_4=AB=5$,所以$OP_4=4+5=9$,所以$P_4(9,0)$.综上所述,x轴上存在点P,使$\triangle ABP$为等腰三角形,P点坐标为(-4,0)或(-1,0)或(9,0)或$\left( \dfrac{7}{8},0\right)$.
【解】
(1)设该一次函数的表达式为$y=kx+b(k\neq 0)$.将B点坐标(0,3)代入得b=3,再将A点坐标(4,0)代入$y=kx+3$,解得$k=-\dfrac{3}{4}$,所以$y=-\dfrac{3}{4}x+3$.
(2)由题意得OA=4,OB=3,所以AB=5.由翻折可得OC=CD,BD=BO=3,所以AD=2.设CD=OC=x,则AC=OA-OC=4-x.在$Rt\triangle ACD$中,由勾股定理得$CD^2+AD^2=AC^2$,即$x^2+2^2=(4-x)^2$,解得$x=\dfrac{3}{2}$,所以C的坐标为$\left( \dfrac{3}{2},0\right)$.设直线BC的表达式为$y=mx+n(m\neq 0)$.将B点坐标(0,3)代入得n=3,再将C点坐标$\left( \dfrac{3}{2},0\right)$代入$y=mx+3$,解得m=-2,所以直线BC的表达式为$y=-2x+3$.
(3)存在.P点坐标为(-4,0)或(-1,0)或(9,0)或$\left( \dfrac{7}{8},0\right)$.

如图,当$AB=P_1B$时,因为AO=4,所以$OP_1=AO=4$,所以$P_1(-4,0)$.当$AB=AP_2$时,$OP_2=AB-AO=1$,所以$P_2(-1,0)$.当$P_3A=P_3B$时,设$OP_3=x$,则$BP_3=4-x$,所以$3^2+x^2=(4-x)^2$,解得$x=\dfrac{7}{8}$,所以$P_3\left( \dfrac{7}{8},0\right)$.当$AB=AP_4$时,$AP_4=AB=5$,所以$OP_4=4+5=9$,所以$P_4(9,0)$.综上所述,x轴上存在点P,使$\triangle ABP$为等腰三角形,P点坐标为(-4,0)或(-1,0)或(9,0)或$\left( \dfrac{7}{8},0\right)$.
4 [较难]如图,在平面直角坐标系中,一次函数$y= -\frac{4}{3}x+4$的图象分别与x轴、y轴交于点A,B,点C在线段OB上,将$\triangle ABC$沿AC翻折,点B恰好落在x轴上的点D处,直线DC交AB于点E.
(1)求点C的坐标.
(2)若点P在直线DC上,点Q是y轴上一点(不与点B重合),当$\triangle CPQ和\triangle CBE$全等时,直接写出点P的坐标:______.(不包括这两个三角形重合的情况)

(1)求点C的坐标.
(2)若点P在直线DC上,点Q是y轴上一点(不与点B重合),当$\triangle CPQ和\triangle CBE$全等时,直接写出点P的坐标:______.(不包括这两个三角形重合的情况)

答案:
【解】
(1)因为$y=-\dfrac{4}{3}x+4$,令x=0,则y=4,令y=0,则x=3,所以A(3,0),B(0,4),所以OA=3,OB=4.因为$\angle AOB=90^\circ$,所以由勾股定理得$AB=\sqrt{OA^2+OB^2}=5$.因为将$\triangle ABC$沿AC翻折,点B恰好落在x轴上的点D处,所以AD=AB=5,所以OD=2.设OC=x,则BC=DC=4-x.在$Rt\triangle OCD$中,由勾股定理得$x^2+2^2=(4-x)^2$,解得$x=\dfrac{3}{2}$,所以$C\left( 0,\dfrac{3}{2}\right)$.
(2)设直线CD的表达式为$y=kx+b(k\neq 0)$.将C点坐标$\left( 0,\dfrac{3}{2}\right)$代入得$b=\dfrac{3}{2}$,再将D点坐标(-2,0)代入$y=kx+\dfrac{3}{2}$,解得$k=\dfrac{3}{4}$,所以直线CD的表达式为$y=\dfrac{3}{4}x+\dfrac{3}{2}$.
因为将$\triangle ABC$沿AC翻折,点B恰好落在x轴上的点D处,所以BC=CD,$\angle ABO=\angle CDO$.因为$\angle BCE=\angle DCO$,所以$\angle BEC=\angle COD=90^\circ$.由
(1)得$OC=\dfrac{3}{2}$,$BC=4-\dfrac{3}{2}=\dfrac{5}{2}$.
①当点D与P重合,点Q与O重合时,$\triangle CPQ\cong \triangle CBE$,此时P(-2,0).
②由①易知$BE=2$,$CE=\dfrac{3}{2}$.如图
(1),
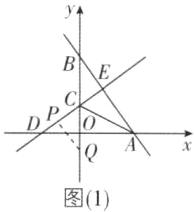
当$CQ=BC=\dfrac{5}{2}$,即点Q的纵坐标为-1,$CE=CP=\dfrac{3}{2}$,$PQ=BE=2$,$\angle CPQ=\angle BEC=90^\circ$时,$\triangle CPQ\cong \triangle CEB$,所以$\dfrac{1}{2}× (-x_P)× \dfrac{5}{2}=\dfrac{1}{2}× \dfrac{3}{2}× 2$,解得$x_P=-\dfrac{6}{5}$,所以$y_P=\dfrac{3}{4}× \left( -\dfrac{6}{5}\right)+\dfrac{3}{2}=\dfrac{3}{5}$,所以$P\left( -\dfrac{6}{5},\dfrac{3}{5}\right)$.
③如图
(2),

当$PQ=BE=2$,$CQ=CE=\dfrac{3}{2}$,$\angle CEB=\angle CQP=90^\circ$时,$\triangle CPQ\cong \triangle CBE$,所以$x_P=2$,所以$y_P=\dfrac{3}{4}× 2+\dfrac{3}{2}=3$,所以P(2,3).
综上所述,点P的坐标为(-2,0)或$\left( -\dfrac{6}{5},\dfrac{3}{5}\right)$或(2,3).
【解】
(1)因为$y=-\dfrac{4}{3}x+4$,令x=0,则y=4,令y=0,则x=3,所以A(3,0),B(0,4),所以OA=3,OB=4.因为$\angle AOB=90^\circ$,所以由勾股定理得$AB=\sqrt{OA^2+OB^2}=5$.因为将$\triangle ABC$沿AC翻折,点B恰好落在x轴上的点D处,所以AD=AB=5,所以OD=2.设OC=x,则BC=DC=4-x.在$Rt\triangle OCD$中,由勾股定理得$x^2+2^2=(4-x)^2$,解得$x=\dfrac{3}{2}$,所以$C\left( 0,\dfrac{3}{2}\right)$.
(2)设直线CD的表达式为$y=kx+b(k\neq 0)$.将C点坐标$\left( 0,\dfrac{3}{2}\right)$代入得$b=\dfrac{3}{2}$,再将D点坐标(-2,0)代入$y=kx+\dfrac{3}{2}$,解得$k=\dfrac{3}{4}$,所以直线CD的表达式为$y=\dfrac{3}{4}x+\dfrac{3}{2}$.
因为将$\triangle ABC$沿AC翻折,点B恰好落在x轴上的点D处,所以BC=CD,$\angle ABO=\angle CDO$.因为$\angle BCE=\angle DCO$,所以$\angle BEC=\angle COD=90^\circ$.由
(1)得$OC=\dfrac{3}{2}$,$BC=4-\dfrac{3}{2}=\dfrac{5}{2}$.
①当点D与P重合,点Q与O重合时,$\triangle CPQ\cong \triangle CBE$,此时P(-2,0).
②由①易知$BE=2$,$CE=\dfrac{3}{2}$.如图
(1),

当$CQ=BC=\dfrac{5}{2}$,即点Q的纵坐标为-1,$CE=CP=\dfrac{3}{2}$,$PQ=BE=2$,$\angle CPQ=\angle BEC=90^\circ$时,$\triangle CPQ\cong \triangle CEB$,所以$\dfrac{1}{2}× (-x_P)× \dfrac{5}{2}=\dfrac{1}{2}× \dfrac{3}{2}× 2$,解得$x_P=-\dfrac{6}{5}$,所以$y_P=\dfrac{3}{4}× \left( -\dfrac{6}{5}\right)+\dfrac{3}{2}=\dfrac{3}{5}$,所以$P\left( -\dfrac{6}{5},\dfrac{3}{5}\right)$.
③如图
(2),

当$PQ=BE=2$,$CQ=CE=\dfrac{3}{2}$,$\angle CEB=\angle CQP=90^\circ$时,$\triangle CPQ\cong \triangle CBE$,所以$x_P=2$,所以$y_P=\dfrac{3}{4}× 2+\dfrac{3}{2}=3$,所以P(2,3).
综上所述,点P的坐标为(-2,0)或$\left( -\dfrac{6}{5},\dfrac{3}{5}\right)$或(2,3).
查看更多完整答案,请扫码查看


