《2025年初中必刷题八年级数学上册北师大版》

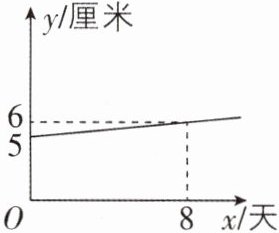
1 [2025 四川成都期末]某生物兴趣小组观察一种植物的生长情况,得到这种植物的高度 y(厘米)与观察时间 x(天)的函数关系图象如图所示.照此计算,该植物的高度生长到 12 厘米需要经过( )


A.16 天
B.32 天
C.40 天
D.56 天

答案： 1.D 【解析】设植物的高度 y(厘米)关于观察时间 x(天)的函数表达式为 y=kx+b. 根据题意,得 b=5,① 6=8k+b,② 将①代入②,得 k=$\frac{1}{8}$,故表达式为 y=$\frac{1}{8}$x+5. 将 y=12 代入 y=$\frac{1}{8}$x+5,解得 x=56. 故该植物的高度生长到12 厘米需要经过 56 天. 故选 D.

2 [2025 河南郑州期末]某电子体重秤的原理是当人站立在秤面上后,应变传感上的应变片发生位移,从而改变电阻值,通过电阻值的变化,即可准确测量体重.简易电子秤制作方法：制作一个装有踏板(踏板质量忽略不计)的可变电阻$ R_1,$已知$ R_1(Ω)$与踏板上人的质量 m(kg)之间的函数关系式为$ R_1 = km + b($其中 k,b 为常数,0 ≤ m ≤ 120),其图象如图所示.下列说法不正确的是( )


A.b = 240
B.可变电阻$ R_1 $随着踏板上人的质量 m 的增加而减小
C.踏板上人的质量 m 每增加 10 kg,可变电阻$ R_1 $减小 20 Ω
D.当可变电阻$ R_1 $为 90 Ω 时,对应测得人的质量 m 为 60 kg

答案： 2.D 【解析】当 m=0 时,R₁=b=240,所以 A 正确,不符合题意. 由图象可知,可变电阻 R₁随着踏板上人的质量 m 的增加而减小,所以 B 正确,不符合题意. 240÷120×10=20(Ω),所以结合图象得踏板上人的质量 m 每增加10 kg,可变电阻 R₁ 减小 20 Ω,所以 C 正确,不符合题意. 将坐标(0,240)和(120,0)分别代入 R₁=km+b,得 b=240,① 120k+b=0,②将①代入②,得 k=-2,所以 R₁=-2m+240(0≤m≤120). 当 R₁=90 时,得-2m+240=90,解得 m=75,所以当可变电阻 R₁ 为 90 Ω 时,对应测得人的质量 m 为 75 kg,所以 D 不正确,符合题意. 故选 D.

3 [2025 湖北黄冈质检]某工厂在生产过程中要消耗大量电能,经过测算,该工厂消耗每千瓦时电产生的利润 y(元)与电价 x(元/千瓦时)有如图所示的一次函数关系,则当该工厂消耗每千瓦时电产生的利润是 180 元时,电价 x 为______元/千瓦时.

答案： 3.600 【解析】设工厂消耗每千瓦时电产生的利润 y 关于电价 x 的函数表达式为 y=kx+n(k≠0). 将(0,300),(500,200)分别代入得n=300,500k+n=200,解得 k=-$\frac{1}{5}$,n=300,所以 y=-$\frac{1}{5}$x+300. 令 y=180,即 180=-$\frac{1}{5}$x+300,解得 x=600,所以当工厂消耗每千瓦时电产生的利润为 180 元时,电价为 600 元/千瓦时. 故答案为 600.

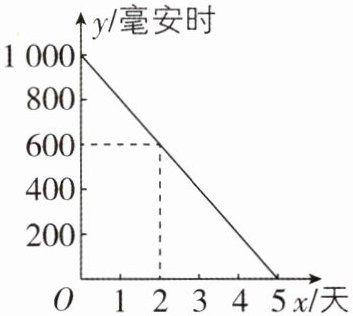
4 [2025 广东深圳校级期中]某手机的电板剩余电量 y(毫安时)是使用天数 x(天)的一次函数,函数图象如图所示.
(1)此种手机的电板最大带电量是______毫安时,在充满电时最多可供手机消耗______天,每天消耗电量______毫安时；
(2)求 y 与 x 之间的函数关系式 y = kx + b,并说出 k 和 b 的实际意义；
(3)若此种手机电量剩余 400 毫安时就会发出提示音,则在手机充满电使用______天后,手机会发出提示音?

答案： 4.【解】
(1)由图象可知,此种手机的电板最大带电量是 1000 毫安时,在充满电时最多可供手机消耗5天. 因为$\frac{1000}{5}$=200(毫安时/天),所以此种手机每天消耗电量 200 毫安时. 故答案为 1000,5,200.
(2)因为一次函数 y=kx+b(0≤x≤5)的图象过点(0,1000)和点(5,0),所以 b=1000,5k+b=0,解得 k=-200,b=1000,所以一次函数的表达式为 y=-200x+1000. k 表示此种手机每天消耗的电量;b 表示此种手机的电板最大带电量.
(3)在 y=-200x+1000 中,令 y=400 得400=-200x+1000,解得 x=3,所以在手机充满电使用 3 天后,手机会发出提示音. 故答案为 3.

5 [2025 福建福州期中]函数 y = -kx + 1(k ≠ 0)的图象如图所示,则方程 -kx + 1 = 0 的解是( )

A.x = -2
B.x = -1
C.x = 0
D.x = 1

答案： 5.A 【解析】由图象可知,函数 y=-kx+1(k≠0)的图象过点(-2,0),所以方程 -kx+1=0 的解为 x=-2. 故选 A.

6 [2025 河北石家庄质检]已知一次函数 y = 2x + n 的图象过点(0,1),则方程 2x + n = 0 的解是______.

答案： 6.x=-$\frac{1}{2}$ 【解析】因为一次函数 y=2x+n 的图象过点(0,1),所以 n=1,所以方程 2x+n=0 可化为 2x+1=0,解得 x=-$\frac{1}{2}$. 故答案为x=-$\frac{1}{2}$.