《2025年初中必刷题八年级数学上册北师大版》

1 [中]若直线$y = 2x + 1与直线y = -x + b$的交点在第一象限,则$b$的值可以是 ( )

A.2
B.1
C.0
D.-1

答案： A 【解析】联立y = 2x + 1与y = -x + b，解得x = $\frac{b - 1}{3}$，y = $\frac{2b + 1}{3}$，所以两直线的交点坐标为($\frac{b - 1}{3}$,$\frac{2b + 1}{3}$). 将四个选项中的b值代入，只有A选项得到的坐标在第一象限，故选A.

2 [2025浙江湖州质检,中]正比例函数$y = kx$($k$为整数)的图象与直线$y = x + 8$的交点恰好是整点(横、纵坐标都是整数的点称为整点),那么满足条件的正比例函数有 ( )

A.5个
B.6个
C.7个
D.无数个

答案： C 【解析】联立得{y = kx, y = x + 8}，解得x = $\frac{8}{k - 1}$，因为x为整数，所以k - 1 = ±8，±4，±2，±1，所以k = 9，-7，5，-3，3，-1，2，0. 又因为k ≠ 0，所以满足条件的k值有7个，即满足条件的正比例函数有7个. 故选C.

3 [2025湖北恩施州质检,中]若方程组$\begin{cases}y = kx + b,\\y = (3k - 1)x + 2\end{cases} $有无穷多组解,则$2k + b^2$的值为____.

答案： 5 【解析】根据题意，得b = 2，3k - 1 = k，解得k = $\frac{1}{2}$，所以2k + b² = 1 + 4 = 5. 故答案为5.

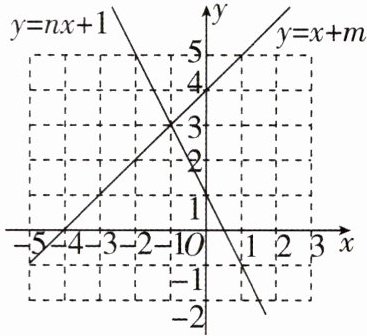
4 [2024贵州遵义调研,较难]如图,在平面直角坐标系中,一次函数$y = x + m的图象和一次函数y = nx + 1的图象分别与y轴交于点(0,4),(0,1)$,则关于$x,y的二元一次方程组\begin{cases}y = x + m - 3,\\y = nx + 1\end{cases} $的解为____.

答案： {x = 0, y = 1} 【解析】因为一次函数y = x + m的图象与y轴交于点(0, 4)，将一次函数y = x + m的图象向下平移3个单位得到一次函数y = x + m - 3的图象，所以一次函数y = x + m - 3的图象与y轴的交点为(0, 1). 因为一次函数y = nx + 1的图象与y轴的交点也是(0, 1)，所以一次函数y = x + m - 3与一次函数y = nx + 1图象的交点为(0, 1)，所以关于x，y的二元一次方程组{y = x + m - 3, y = nx + 1}的解为{x = 0, y = 1}. 故答案为{x = 0, y = 1}.

5 [中]如图,直线$l_1:y = 2x + 1与直线l_2:y = mx + 4相交于点P(1,b)$,直线$l_1,l_2与x轴分别交于A,B$两点.
(1)求$b,m$的值,并结合图象写出关于$x,y的方程组\begin{cases}2x - y = -1,\\mx - y = -4\end{cases} $的解;
(2)求$\triangle ABP$的面积;
(3)垂直于$x轴的直线x = a与直线l_1,l_2分别交于点C,D$,若线段$CD$的长为2,求$a$的值.

答案： 【解】
(1)把点P(1, b)代入y = 2x + 1，得b = 2 + 1 = 3，所以P(1, 3). 把点P(1, 3)代入y = mx + 4，得m + 4 = 3，所以m = -1. 因为直线l₁: y = 2x + 1与直线l₂: y = mx + 4相交于点P(1, 3)，所以方程组{2x - y = -1, mx - y = -4}的解为{x = 1, y = 3}.
(2)因为l₁: y = 2x + 1，l₂: y = -x + 4，所以A(-$\frac{1}{2}$, 0)，B(4, 0)，所以AB = 4 - (-$\frac{1}{2}$) = $\frac{9}{2}$，所以S△ABP = $\frac{1}{2}$AB·yP = $\frac{1}{2}$×$\frac{9}{2}$×3 = $\frac{27}{4}$.
(3)直线x = a与直线l₁的交点C为(a, 2a + 1)，与直线l₂的交点D为(a, -a + 4). 因为CD = 2，所以|2a + 1 - (-a + 4)| = 2，即|3a - 3| = 2，所以3a - 3 = 2或3a - 3 = -2，所以a = $\frac{5}{3}$或$\frac{1}{3}$.
关键点拨：
(3)根据图象可得，线段CD长为2的情况有两种，注意分类讨论，不要漏解.
思路分析：设该一次函数的表达式为y = kx + b. 由一次函数y = kx + b的图象与正比例函数y = 2x的图象平行，可知k = 2，再求出直线y = 3x + 4与y轴交于点(0, 4)，将点(0, 4)代入一次函数y = 2x + b中求出b的值，即可得出答案.

6 思想方法数形结合[2024山东青岛期中,较难]我们知道,二元一次方程有无数个解. 在平面直角坐标系中,我们标出以某个二元一次方程的解为坐标的点,就会发现这些点在同一条直线上.
例如:$\begin{cases}x = 1,\\y = 2\end{cases} 是方程x - y = -1$的一个解,对应点为$M(1,2)$. 如图所示,我们在平面直角坐标系中将其标出,该方程的其他解还对应点$(2,3),(3,4)……$将这些点连起来,可以发现它们在同一条直线上,反过来,在这条直线上任取一点,这个点的坐标也是方程$x - y = -1$的解,所以我们把这条直线叫作方程$x - y = -1$的图象.
一般地,以二元一次方程的解为坐标的点连成的直线就叫这个方程的图象. 请解答下列问题:
(1)已知$A(1,1),B(-3,4),C(\frac{1}{2},2)$,则点____(填“A”或“B”或“C”)在方程$2x - y = -1$的图象上.
(2)求方程$2x + 3y = 9和方程3x - 4y = 5$图象的交点坐标.
(3)已知以关于$x,y的方程组\begin{cases}5x + 3y = 20 + 7m,\\3x + 4y = 19 - 14m\end{cases} 的解为坐标的点在方程x + y = 5$的图象上,当$t ＞ m$时,化简$\sqrt{(-t - 2)^2} - |1 - 7t|$.

答案： 【解】
(1)因为2×1 - 1 = 1 ≠ -1，2×(-3) - 4 = -10 ≠ -1，2×$\frac{1}{2}$ - 2 = -1，所以点C在方程2x - y = -1的图象上. 故答案为C.
(2)由{2x + 3y = 9, 3x - 4y = 5}，解得{x = 3, y = 1}，所以方程2x + 3y = 9和方程3x - 4y = 5图象的交点坐标为(3, 1).
(3)由{5x + 3y = 20 + 7m, 3x + 4y = 19 - 14m}，解得{x = $\frac{23 + 70m}{11}$, y = $\frac{35 - 91m}{11}$}. 因为x + y = 5，所以$\frac{23 + 70m}{11}$ + $\frac{35 - 91m}{11}$ = 5，所以m = $\frac{1}{7}$. 当t ＞ $\frac{1}{7}$时，$\sqrt{(-t - 2)^2}$ - |1 - 7t| = t + 2 + 1 - 7t = 3 - 6t.