《2025年初中必刷题八年级数学上册北师大版》

1[中]如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点$(-1,1)$,第2次接着运动到点$(-2,0)$,第3次接着运动到点$(-3,2),...$,按这样的运动规律,经过第2023次运动后,动点P的坐标是( )


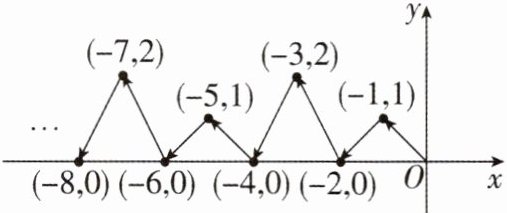
A.$(-2023,0)$
B.$(-2023,1)$
C.$(-2023,2)$
D.$(2023,0)$

答案： C 【解析】动点P的运动规律可以看成每运动4次为一个循环,每个循环向左移动4个单位.点P的横坐标为运动次数的相反数,纵坐标每4次一循环,依次是1,0,2,0.因为2023=505×4+3,所以经过第2023次运动后,动点P的横坐标为-2023,纵坐标为2,即P(-2023,2),故选C.

2[2025安徽安庆期末,中]如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆$O_{1}$,半圆$O_{2}$,半圆$O_{3}$,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac {π}{2}$个单位长度,则第2021秒时,点P的坐标是( )


A.$(2020,0)$
B.$(2021,-1)$
C.$(2021,1)$
D.$(2022,0)$

答案： C 【解析】半径为1个单位长度的半圆的周长为$\frac{1}{2}×2\pi×1=\pi$.因为点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{\pi}{2}$个单位长度,所以点P每秒走$\frac{1}{2}$个半圆.当点P运动时间为1秒时,点P的坐标为(1,1);当点P运动时间为2秒时,点P的坐标为(2,0);当点P运动时间为3秒时,点P的坐标为(3,-1);当点P运动时间为4秒时,点P的坐标为(4,0);当点P运动时间为5秒时,点P的坐标为(5,1);当点P运动时间为6秒时,点P的坐标为(6,0);…因为2021÷4=505……1,所以点P的坐标是(2021,1),故选C.

3[2025山东烟台质检,中]在平面直角坐标系中,对于点$P(x,y)$,我们把点$P'(-y+1,x+1)$称为点P的伴随点.已知点$A_{1}的伴随点为A_{2}$,点$A_{2}的伴随点为A_{3}$,点$A_{3}的伴随点为A_{4}$,…,这样依次得到点$A_{1},A_{2},A_{3},...,A_{n}$.若点$A_{1}的坐标为(2,4)$,则点$A_{2022}$的坐标为( )

A.$(3,-1)$
B.$(-2,-2)$
C.$(-3,3)$
D.$(2,4)$

答案： C 【解析】因为$A_1$的坐标为(2,4),所以$A_2$(-3,3),$A_3$(-2,-2),$A_4$(3,-1),$A_5$(2,4),…,依次类推,每4个点为一个循环组依次循环.因为2022=505×4+2,所以点$A_{2022}$的坐标与$A_2$の坐标相同,为(-3,3).故选C.

4[中]如图,一机器人从原点出发按图示方向做折线运动,第1次从原点运动到$A_{1}(1,0)$,第2次运动到$A_{2}(1,1)$,第3次运动到$A_{3}(-1,1)$,第4次运动到$A_{4}(-1,-1)$,第5次运动到$A_{5}(2,-1),...$,则第15次运动到的点$A_{15}$的坐标是( )

A.$(4,4)$
B.$(-4,4)$
C.$(-4,3)$
D.$(5,-4)$

答案： B【解析】每一象限的点的特点:第一象限:$A_2$(1,1),$A_6$(2,2),$A_{10}$(3,3),...,$A_{4n+2}$(n+1,n+1);第二象限:$A_3$(-1,1),$A_7$(-2,2),...,$A_{4n+3}$(-n -1,n +1);第三象限:$A_4$(-1,-l),$A_8$(-2,-2),...,$A_{4n}$(-n,-n);第四象限:$A_5$(2,-1),$A_9$(3,-),...,$A_{n+1}$(n +1,-n).
∵15=4×3+3,
∴$A_{15}$在第二象限,坐标为(-4,4).

5[2025辽宁大连调研,中]如图,在平面直角坐标系中,有若干个整数点,其顺序按图中箭头方向排列,即$(0,1),(0,2),(1,2),(1,3),(0,3),(-1,3),...$,根据这个规律,探索可得第100个点的坐标为( )

A.$(2,14)$
B.$(-2,13)$
C.$(3,14)$
D.$(-3,13)$

答案： A【解析】第一步(0,1),纵坐标是1的点共1个;(0,), (1,2),纵坐标是2的点共2个;(1,3),(0,3),(-l,),纵坐标是的点共个;...,依次类推,纵坐标是n的点共有n个.从第2个点开始,纵坐标是奇数的从右到左计数,最左边点的横坐标为$-\frac{(n -1)}{2}$;纵坐标是偶数的从左到右计数,最右边点的横坐标为$\frac{n}{2}$.第二步 纵坐标是1到纵坐标是n的点共有1+2+3+…+n=$\frac{n(n +1)}{2}$个.第三步当n=13时,$\frac{13×(13 +1)}{2}=91$,当n=14时,$\frac{14×(14 +1)}{2}=105$,所以n=14.第四步由上可知第100个点的纵坐标为14,根据n=14这一行の规律:共有14个点,从左到右计数,最右边点的横坐标为$\frac{n}{2}$,所以14÷2=7,所以第105个点的坐标为(7,14),第104个点的坐标为(6,14),第103个点的坐标为(5,14),第102个点的坐标为(4,14),第101个点的坐标为(3,14),第100个点的坐标为(2,14),故选A.

6[中]如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次平移一个单位,得到点$A_{1}(0,1),A_{2}(1,1),A_{3}(1,0),A_{4}(2,0),...$,那么点$A_{21}$的坐标为____.

答案： (10,1) 【解析】由题图可得,点$A_{4n+1}$(2n,1)(n为自然数),21=4×5+1,则$A_{21}$ 的坐标是(10,1).故答案为(10,1).