第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1 [中]某校八年级学生的平均年龄为 14 岁,年龄的方差为 3,若学生人数没有变动,则对两年后的同一批学生年龄的说法正确的是 ( )
A.平均年龄为 14 岁,方差改变
B.平均年龄为 16 岁,方差不变
C.平均年龄为 16 岁,方差改变
D.平均年龄为 14 岁,方差不变
A.平均年龄为 14 岁,方差改变
B.平均年龄为 16 岁,方差不变
C.平均年龄为 16 岁,方差改变
D.平均年龄为 14 岁,方差不变
答案:
B
2 [中]某天的体育课上,老师测量了某班同学的身高,恰巧小明这日请假没来,经过计算得知,除了小明外,该班其他同学身高的平均数为 170 cm,方差为 a.第二天,小明来到学校,老师帮他补测了身高,发现他的身高也是 170 cm,此时全班同学身高的方差为 b,那么 a 与 b 的大小关系是 a____b.(填“<”“>”或“=”)
答案:
>
3 [中]某选手在比赛中的成绩(单位:分)分别是 90,87,92,88,93,方差是 5.2,如果去掉一个最高分和一个最低分,那么该选手成绩的方差会____(填“变大”“变小”“不变”或“不能确定”).
答案:
变小
4 [较难]为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |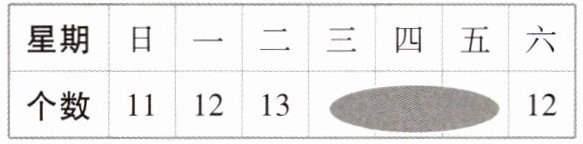
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一的众数是 13,平均数是 12,那么这组数据的方差是____.
| 星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |

其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一的众数是 13,平均数是 12,那么这组数据的方差是____.
答案:
$\frac {8}{7}$
5 [2025 湖南湘西州期末,中]已知数据 $ x _ { 1 } , x _ { 2 } , x _ { 3 } $ 的平均数是 10,方差是 6,那么数据 $ x _ { 1 } + 3 , x _ { 2 } + 3 , x _ { 3 } + 3 $ 的平均数和方差分别是 ( )
A.13,6
B.13,9
C.10,6
D.10,9
A.13,6
B.13,9
C.10,6
D.10,9
答案:
A
6 [2025 吉林长春质检,中]小明计算出一组数据的方差为 $ s ^ { 2 } $ ,小丽将这组数据中每个数据都除以 2,所得新数据的方差是 ( )
A.$ \frac { 1 } { 2 } s ^ { 2 } $
B.$ 2 s ^ { 2 } $
C.$ \frac { 1 } { 4 } s ^ { 2 } $
D.$ 4 s ^ { 2 } $
A.$ \frac { 1 } { 2 } s ^ { 2 } $
B.$ 2 s ^ { 2 } $
C.$ \frac { 1 } { 4 } s ^ { 2 } $
D.$ 4 s ^ { 2 } $
答案:
C
7 [2025 山东威海期中,中]一组数据 $ a - 1 , b - 1 , c - 1 , d - 1 , e - 1 , f - 1 , g - 1 $ 的平均数是 m,方差是 n,则另一组数据 $ 2 a - 3 , 2 b - 3 , 2 c - 3 , 2 d - 3 , 2 e - 3 , 2 f - 3 , 2 g - 3 $ 的平均数是____,方差是____.
答案:
$2m-1$ $4n$
8 核心素养 应用意识 [2025 江苏盐城质检,中]某校要从新入学的两名体育特长生李勇、张浩中挑选一人参加校级跳远比赛,在跳远专项测试以及之后的 6 次跳远选拔赛中,他们的成绩(单位:cm)如下表所示:
| | 专项测试成绩和 6 次跳远选拔赛成绩 | 平均数 | 方差 |
| 李勇 | 603 589 602 596 604 612 608 | 602 | |
| 张浩 | 597 580 597 630 590 631 596 | | 333 |
(1)求张浩同学 7 次成绩的平均数和李勇同学 7 次成绩的方差(结果保留整数).
(2)请你分别从平均数和方差的角度分析两人成绩的特点.
(3)经查阅历届比赛的资料,成绩若达到 6.00 m,就很可能得到冠军,你认为应选谁去参赛夺冠比较有把握?请说明理由.
(4)以往的该项最好成绩的纪录是 6.15 m,若想要打破纪录,你认为应选谁去参赛?
| | 专项测试成绩和 6 次跳远选拔赛成绩 | 平均数 | 方差 |
| 李勇 | 603 589 602 596 604 612 608 | 602 | |
| 张浩 | 597 580 597 630 590 631 596 | | 333 |
(1)求张浩同学 7 次成绩的平均数和李勇同学 7 次成绩的方差(结果保留整数).
(2)请你分别从平均数和方差的角度分析两人成绩的特点.
(3)经查阅历届比赛的资料,成绩若达到 6.00 m,就很可能得到冠军,你认为应选谁去参赛夺冠比较有把握?请说明理由.
(4)以往的该项最好成绩的纪录是 6.15 m,若想要打破纪录,你认为应选谁去参赛?
答案:
(1)张浩同学7次成绩的平均数为603cm,李勇同学7次成绩的方差约为49;
(2)从成绩的平均数来看,张浩成绩的“平均水平”比李勇高;从成绩的方差来看,李勇的成绩比张浩的更稳定;
(3)应选李勇去参赛夺冠比较有把握,理由:在跳远专项测试以及之后的6次跳远选拔赛中,李勇有5次成绩超过6m,而张浩只有2次超过6m,且从成绩的方差来看,李勇的成绩比张浩更稳定;
(4)应选张浩去参赛.
(1)张浩同学7次成绩的平均数为603cm,李勇同学7次成绩的方差约为49;
(2)从成绩的平均数来看,张浩成绩的“平均水平”比李勇高;从成绩的方差来看,李勇的成绩比张浩的更稳定;
(3)应选李勇去参赛夺冠比较有把握,理由:在跳远专项测试以及之后的6次跳远选拔赛中,李勇有5次成绩超过6m,而张浩只有2次超过6m,且从成绩的方差来看,李勇的成绩比张浩更稳定;
(4)应选张浩去参赛.
查看更多完整答案,请扫码查看


