《2025年初中必刷题八年级数学上册北师大版》

1 [中]已知正比例函数 $ y = (m - 2)x $ 的图象上两点 $ A(x_1,y_1) $, $ B(x_2,y_2) $,当 $ x_1 - x_2 ＜ 0 $ 时, $ y_1 - y_2 ＞ 0 $,那么 $ m $ 的取值范围是 ( )

A.$ m ＜ 2 $
B.$ m ＞ 2 $
C.$ m ＜ 0 $
D.$ m ＞ 0 $

答案： A [解析]已知正比例函数y=(m - 2)x的图象上两点$A(x_{1},y_{1})$，$B(x_{2},y_{2})$，当$x_{1}-x_{2}＜0$时，$y_{1}-y_{2}＞0$，所以y随x的增大而减小，所以m - 2＜0，则m＜2.故选A.

2 [中]在平面直角坐标系中,若一个正比例函数的图象经过 $ (a,3) $, $ (4,b) $ 两点,则 $ a $, $ b $ 一定满足的关系式为 ( )

A.$ a - b = 1 $
B.$ a + b = 7 $
C.$ ab = 12 $
D.$ \frac{a}{b} = \frac{3}{4} $

答案： C [解析]设正比例函数的表达式为y = kx.将(a,3)，(4,b)代入函数表达式中，得3 = ak，b = 4k，所以$k=\frac{3}{a}=\frac{b}{4}$，所以ab = 12.故选C.

3 [2024 陕西宝鸡期末,中]如图,点 $ B $ 在直线 $ y = 2x $ 上,过点 $ B $ 作 $ BA \perp x $ 轴于点 $ A $,作 $ BC // x $ 轴与直线 $ y = kx(k \neq 0) $ 交于点 $ C $,若 $ AB:BC = 1:2 $,则 $ k $ 的值是 ( )

A.$ \frac{2}{7} $
B.$ \frac{2}{3} $
C.$ \frac{1}{3} $
D.$ \frac{2}{5} $

答案： D [解析]设OA = a.因为点B在直线y = 2x上，BA⊥x轴，所以y = 2a，所以AB = 2a.因为AB:BC = 1:2，所以BC = 4a.因为BC//x轴，所以C(5a,2a).因为点C在直线y = kx(k≠0)上，所以$2a = 5ak$，所以$k=\frac{2}{5}$，故选D.

4 新考向 跨学科综合 [2025 江西吉安期末,中]如图表示光线从空气进入水中时的光路图,若按如图所示的方式建立平面直角坐标系,并设入水前与入水后光线所在直线的函数表达式分别为 $ y_1 = k_1x $, $ y_2 = k_2x $,则关于 $ k_1 $ 与 $ k_2 $ 的关系,下列说法正确的是 ( )

A.$ k_1 ＞ 0 $, $ k_2 ＜ 0 $
B.$ k_1 ＞ 0 $, $ k_2 ＞ 0 $
C.$ |k_1| ＞ |k_2| $
D.$ k_1 - k_2 ＞ 0 $

答案： D [解析]由题图可知，$y_{1}$随x的增大而减小，$y_{2}$随x的增大而减小，所以$k_{1}＜0$，$k_{2}＜0$，故选项A、B错误;根据直线越陡，$\vert k\vert$越大可知，$\vert k_{1}\vert＜\vert k_{2}\vert$，所以$k_{1}＞k_{2}$，所以$k_{1}-k_{2}＞0$，故选项C错误，选项D正确.故选D.

5 [2024 江苏镇江质检,中]已知正比例函数 $ y = kx(k ＜ 0) $,当 $ 1 \leq x \leq 3 $ 时,函数 $ y $ 的最大值和最小值之差为 4,则 $ k = $______.

答案： -2 [解析]因为正比例函数y = kx(k＜0)，所以y随x的增大而减小，当x = 1时，y = k;当x = ;当x = 3时，y = 3k.因为当1≤x≤3时，函数y的最大值和最小值之差为4，所以k - 3k = 4，解得k = -2.故答案为-2.

6 [中]直线 $ y = 2x $ 上到 $ x $ 轴的距离为 2 的点的坐标为______.

答案： (1,2)或(-1,-2) [解析]因为直线y = 2x上的点到x轴的距离是2，所以y = ±2.当y = 2时，即2x = 2，解得x = 1;当y = -2时，即2x = -2，解得x = -1，所以符合条件的点的坐标为(1,2)或(-1,-2).

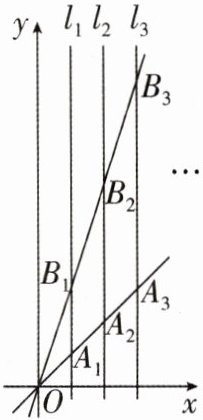
7 [2024 江苏连云港质检,中]如图,直线 $ l_1 \perp x $ 轴于点 $ (1,0) $,直线 $ l_2 \perp x $ 轴于点 $ (2,0) $,直线 $ l_3 \perp x $ 轴于点 $ (3,0) $,…,直线 $ l_n \perp x $ 轴于点 $ (n,0) $ ($ n \geq 2 $ 且 $ n $ 为整数).函数 $ y = x $ 的图象与直线 $ l_1 $, $ l_2 $, $ l_3 $,…, $ l_n $ 分别交于点 $ A_1 $, $ A_2 $, $ A_3 $,…, $ A_n $;函数 $ y = 3x $ 的图象与直线 $ l_1 $, $ l_2 $, $ l_3 $,…, $ l_n $ 分别交于点 $ B_1 $, $ B_2 $, $ B_3 $,…, $ B_n $,如果 $ \triangle OA_1B_1 $ 的面积记作 $ S_1 $,四边形 $ A_1A_2B_2B_1 $ 的面积记作 $ S_2 $,四边形 $ A_2A_3B_3B_2 $ 的面积记作 $ S_3 $,…,四边形 $ A_{n - 1}A_nB_nB_{n - 1} $ 的面积记作 $ S_n $,那么 $ S_{2024} = $______.

答案： 4047 [解析]根据题意得，$A_{n - 1}B_{n - 1}=3(n - 1)-(n - 1)=3n - 3 - n + 1 = 2n - 2$，$A_{n}B_{n}=3n - n = 2n$.因为直线$l_{n - 1}⊥x$轴于点(n - 1,0)，直线$l_{n}⊥x$轴于点(n,0)，所以$A_{n - 1}B_{n - 1}//A_{n}B_{n}$，且$l_{n - 1}$与$l_{n}$间的距离为1，所以四边形$A_{n - 1}A_{n}B_{n}B_{n - 1}$是梯形$S_{n}=\frac{1}{2}(2n - 2 + 2n)×1=\frac{1}{2}(4n - 2)=2n - 1$.当n = 2024时，$S_{2024}=2×2024 - 1 = 4047$.故答案为4047.

8 [较难]如图,在平面直角坐标系中,点 $ A $ 的坐标为 $ (1,2) $,点 $ B $ 是正比例函数 $ y = x $ 图象上一动点,点 $ C $ 是 $ y $ 轴上一动点,则 $ \triangle ABC $ 周长的最小值为______.

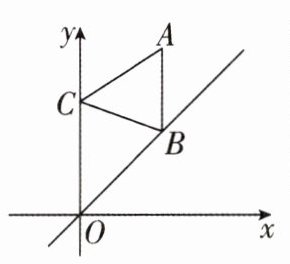
答案： $\sqrt{10}$

9 思想方法 数形结合 [2025 北京西城区校级期中,中]函数问题:
(1)已知函数 $ y = 2|x| $.
①自变量 $ x $ 的取值范围是______.
②将下表补充完整,并在平面直角坐标系中画出函数 $ y = 2|x| $ 的图象:
| $ x $ | …$ $ | $ -2 $ | $ -1 $ | $ 0 $ | $ 1 $ | $ 2 $ | …$ $ |
| $ y $ | …$ $ | | | | | | …$ $ |
③当自变量 $ x $ 的值从 1 增加到 2 时,函数 $ y $ 的值增加了______.
(2)在一个变化的过程中,变量 $ x $ 与 $ y $ 之间可能是函数关系,也可能不是函数关系.下列各式中, $ y $ 是 $ x $ 的函数的是______.
① $ x + y = 1 $;② $ |x + y| = 1 $;③ $ xy = 1 $;④ $ x^2 + y^2 = 1 $.

答案：
[解]
(1)①自变量x的取值范围是任意实数.故答案为任意实数.
②分别将x = -2，-1，0，1，2代入$y = 2\vert x\vert$，得y = 4，2，0，2，4.故答案为4，2，0，2，4;函数$y = 2\vert x\vert$的图象如图所示.

③当自变量x的值从1增加到2时，函数y的值增加了2.故答案为2.
(2)根据函数的定义可知，①③中对于变量x的每一个值，变量y都有唯一的值与它对应，故y是x的函数的是①③.故答案为①③.