《2025年初中必刷题八年级数学上册北师大版》

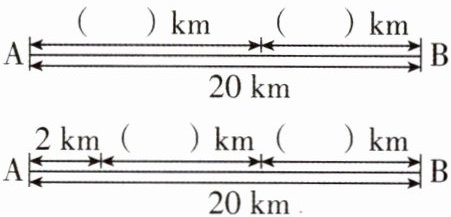
1 [2025 江苏无锡调研,中]A、B 两地间的路程为 20 km,甲、乙两人同时相对而行,2 h 后相遇,相遇后甲就返回 A 地,乙仍向 A 地前进,甲回到 A 地时,乙离 A 地还有 2 km,求甲、乙两人的速度.设甲的速度为 x km/h,乙的速度为 y km/h,先在下列线段图中的括号内填入适当代数式,再解决问题.

答案：
【解】因为甲、乙两人同时相对而行，2h后相遇，且甲的速度为xkm/h，乙的速度为ykm/h，则相遇时甲的路程为2xkm，乙的路程为2ykm。因为相遇后甲就返回A地，乙仍向A地前进，甲回到A地时，乙离A地还有2km，所以甲回到A地后，乙又行了2ykm。将各代数式填入括号内，如图所示。
　　　　　　　　　
根据题意得{2x + y = 20,2x - 2y = 2}，解得{x = 5.5,y = 4.5}。
答：甲的速度为5..5km/h，乙的速度为4.5km/h。

2 [2025 山东青岛质检,中]有一座大桥全长 920 米,其中主桥长 800 米,小明乘列车匀速经过这座桥,为了探究该列车的长度与速度,记录了以下两个数据:①列车完全在主桥上的时间为 35 秒.②列车上主桥到完全通过主桥用了 45 秒.知道这两个数据后,请你帮小明算出该列车的长度与速度.

答案： 【解】设该列车的长度为x米，速度为y米/秒。根据题意可得{35y = 800 - x,45y = 800 + x}，解得{x = y = 20}。
答：该列车的长度为100米，速度为20米/秒。

3 [2025 湖南怀化期末,中]甲、乙两地相距 74 千米,途中有上坡、平路和下坡.一汽车下午 1 时从甲地出发,到乙地时是下午 3 时 30 分,停留 30 分钟后从乙地出发,下午 6 时 48 分返回甲地.已知汽车在上坡每小时行驶 20 千米,平路每小时行驶 30 千米,下坡每小时行驶 40 千米,求甲地到乙地的途中平路、上坡、下坡分别是多少千米.

答案： 解：设甲地到乙地的上坡路为$x$千米，平路为$y$千米，下坡路为$z$千米。
从甲地到乙地用时：下午3时30分 - 下午1时 = 2.5小时，从乙地返回甲地用时：下午6时48分 - （下午3时30分 + 30分钟）= 2.8小时。
根据题意可列方程组：
$\begin{cases}x + y + z = 74 \\frac{x}{20} + \frac{y}{30} + \frac{z}{40} = 2.5 \\frac{z}{20} + \frac{y}{30} + \frac{x}{40} = 2.8\end{cases}$
整理第二个方程：两边同乘120得$6x + 4y + 3z = 300$；
整理第三个方程：两边同乘120得$6z + 4y + 3x = 336$。
用整理后的第三个方程减去第二个方程得：$3z - 3x = 36$，即$z - x = 12$，$z = x + 12$。
将$z = x + 12$代入第一个方程得：$x + y + x + 12 = 74$，$2x + y = 62$，$y = 62 - 2x$。
把$z = x + 12$，$y = 62 - 2x$代入$6x + 4y + 3z = 300$得：
$6x + 4(62 - 2x) + 3(x + 12) = 300$，
$6x + 248 - 8x + 3x + 36 = 300$，
$x + 284 = 300$，$x = 16$。
则$y = 62 - 2×16 = 30$，$z = 16 + 12 = 28$。
答：甲地到乙地的途中平路是30千米，上坡是16千米，下坡是28千米。

4 [2025 内蒙古呼伦贝尔期末,中]甲、乙二人都以不变的速度在环形跑道上跑步,如果同时同地出发,反向而行,每隔 2 分钟相遇一次;如果同时同地出发,同向而行,每隔 4 分钟相遇一次.已知甲比乙跑得慢,甲、乙二人每分钟各跑多少圈?

答案： 【解】设乙每分钟跑x圈，甲每分钟跑y圈。由题意得$\begin{cases}2x+2y=1\\4x-4y=1\end{cases}$，解得$\begin{cases}x=\frac{3}{8}\\y=\frac{1}{8}\end{cases}$。
答：乙每分钟跑$\frac{3}{8}$圈，甲每分钟跑$\frac{1}{8}$圈。

5 [2025 湖南邵阳质检,中]甲、乙两班同时从学校 A 出发去距离学校 75 km 的军营 B 军训,甲班学生步行速度为 4 km/h,乙班学生步行速度为 5 km/h,学校有一辆汽车,该车空车速度为 40 km/h,载人时的速度为 20 km/h,且这辆汽车一次只能载一个班的学生,现在要求两个班的学生同时到达军营,问他们至少需要多久才能到达?

答案：
【解】如图。
　　
设甲班学生从学校A乘汽车出发a km至E处后下车步行至军营B，空车返回至C处，此时乙班学生已步行b km，乙班学生于C处上车并乘车至军营B处，则$\begin{cases}\frac{a}{20}+\frac{a-b}{40}=\frac{b}{5}\frac{a-b}{0}+\frac{75-b}{20}=\frac{75-a}{4}\end{cases}$，解得$\begin{cases}a=0\\b=0\end{cases}$则至少需要$\frac{60}{20}+\frac{75-60}{4}=6.75$(h)。
答：他们至少需要6.75h才能到达。