《2025年初中必刷题八年级数学上册北师大版》

1 [中]已知一次函数$y= kx-2k+1(k≠0)$,回答下列问题：
(1)若该函数的图象过原点,求$k$的值.
(2)无论$k$取何值,该函数的图象总经过一个定点,请你求出这个定点的坐标.

答案： 1.【解】
(1)因为一次函数y=kx - 2k + 1的图象过原点，所以 - 2k + 1 = $\frac{1}{2}$。
(2)因为y = kx - 2k + 1 = k(x - 2) + 1，所以(x - 2)k = y - 1。因为无论k取何值，该函数图象总经过一个定点，即关于k的方程(x - 2)k = y - 1有无数个解，所以x - 2 = 0，y - 1 = 0，解得x = 2，y = 1,所以这个定点的坐标为(2,1)。

2 [2025江苏南京质检,中]已知一次函数$y_{1}= ax+3a+2$($a$为常数,$a≠0$)和$y_{2}= x+1$.
(1)当$a= -1$时,求两个函数图象的交点坐标；
(2)不论$a$为何值,$y_{1}= ax+3a+2$($a$为常数,$a≠0$)的图象都经过一个定点,则这个定点坐标是____；
(3)若两个函数图象的交点在第三象限,结合图象,直接写出$a$的取值范围.

答案：
2.【解】
(1)当a = - 1时，y₁ = - x - 1。令y₁ = y₂，得 - x - 1 = x + 1，解得x = - 1。当x = - 1时，y₁ = - (- 1) - 1 = 0，所以当a = - 1时，两个函数图象的交点坐标为(- 1,0)。
(2)y₁ = ax + 3a + 2 = a(x + 3) + 2。由题意得x + 3 = 0，解得x = - 3，此时，y₁ = 2，所以不论a为何值，y₁ = ax + 3a + 2(a为常数，a≠0)的图象都经过定点(- 3,2)，故答案为(- 3,2)。
(3)a ＜ - 1或a ＞ 1。由
(2)得y₁ = ax + 3a + 2的图象过定点(- 3,2)。画出函数图象如图所示:

当直线y₁过点(- 1,0)时， - a + 3a + 2 = 0，解得a = - 1。当直线y₁与y₂平行时，a = 1。结合图象可知，若两个函数图象的交点在第三象限，则a的取值范围是a ＜ - 1或a ＞ 1。

3 [中]如图所示,直线$y= x+4与两坐标轴分别交于A$,$B$两点,点$C是OB$的中点,$D$,$E分别是直线AB和y$轴上的动点,则$\triangle CDE$周长的最小值是____.

答案：
2$\sqrt{10}$ 【解析】如图，作点C关于AB的对称点F，关于AO的对称点G，连接DF，EG，FB，FC，FG。因为直线y = x + 4与两坐标轴分别交于A，B两点，所以令x = 0，则y = 4，令y = 0，则x = - 4，所以A(0,4)，B(- 4,0)，所以OA = OB = 4。又因为点C是OB的中点，所以OC = BC = $\frac{1}{2}$OB = 2。因为点C与点G关于AO对称，所以OG = OC = 2,EC = EG，所以BG = OB + OG = 6。因为OA = OB，∠AOB = 90°，所以∠ABC = ∠BAO = 45°。又因为点C与点F关于AB对称，所以∠ABC = ∠ABF = 45°，BC = BF = 2，DF = DC，所以∠FBC = 90°。因为DF = DC，EC = EG，所以△CDE的周长为CD + DE + CE = DF + DE + EG ≥ FG，当点F，D，E，G在同一直线上时，△CDE的周长最小，为FG的长。因为在Rt△BFG中，FG = $\sqrt{BF² + BG²}$ = 2$\sqrt{10}$，所以△CDE周长的最小值是2$\sqrt{10}$。故答案为2$\sqrt{10}$。

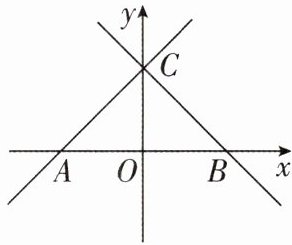
4 [2025广东广州质检,中]如图,直线$y= x+3与两坐标轴分别交于点A$,$C$,直线$BC与直线AC关于y$轴对称.
(1)求点$A$,$B$,$C$的坐标；
(2)若过点$O的直线l将\triangle ABC分成面积之比为1∶2$的两部分,求该直线的表达式.

答案：
4.【解】
(1)在y = x + 3中，令x = 0，得y = 3，令y = 0，得x = - 3，所以A(- 3,0)，C(0,3)。因为直线BC与直线AC关于y轴对称，所以点B与点A关于y轴对称，所以B点坐标为(3,0)思路分析
(2)分两种情况:①设直线l交AC于K，当S△AOK : S四边形KOBC = 1 : 2时，过K作KH⊥AB于H，求得K点坐标，即可求解；②设直线l交BC于T，当S△BOT : S四边形AOTC = 1 : 2时，同理可解。
关键点拨 熟练掌握“将军饮马”模型是解题的关键。
(2)由
(1)得A(- 3,0)，C(0,3)，B(3,0)，所以OA = OB = OC = 3，AB = 6，所以S△ABC = $\frac{1}{2}$×6×3 = 9。①设直线l交AC于K，当S△AOK : S四边形KOBC = 1 : 2时，过K作KH⊥AB于H，如图
(1)，所以S△AOK = $\frac{1}{3}$S△ABC = 3，所以$\frac{1}{2}$OA·HK = 3，所以KH = 2。对于y = x + 3，令y = 2，得x = - 1，所以K(- 1,2)。设直线l的表达式为y = px(p≠0)，将K(- 1,2)代入，得2 = - p，解得p = - 2，所以直线l的表达式为y = - 2x。②设直线l交BC于T，当S△BOT : S四边形AOTC = 1 : 2时，过T作TH'⊥AB于H'，如图
(2)，同理可得TH' = 2。易得直线BC的表达式为y = - x + 3。对于y = - x + 3，令y = 2，得x = 1，所以T(1,2)，易得直线l的表达式为y = 2x综上所述，直线l的表达式为y = - 2x或y = 2x。

5 [2025江苏南通期中,较难]在平面直角坐标系$xOy$中,一次函数$y= kx-2k$($k$为常数,且$k≠0$)的图象分别交$x$轴、$y轴于点A$,$B$.
(1)点$A$的坐标为____,点$B$的坐标为____(用含有$k$的式子表示).
(2)若一次函数$y= kx-2k的图象经过点(1,-2)$,平行于$x轴的两条直线l_{1}$,$l_{2}分别与一次函数y= kx-2k的图象交于点M$,$N$,点$M$,$N的横坐标分别为m$,$n$.当$m-n= 3$时,线段$MN$的长度是否发生变化？若不变,请求出$MN$的长度；若变化,请说明理由.
(3)若一次函数$y= kx-2k的图象与函数y= x的图象及x轴所围成的三角形的面积不小于1$,求$k$的取值范围.

答案：
5.【解】
(1)在y = kx - 2k(k为常数，且k≠0)中，令y = 0，得x = 2；令x = 0，得y = - 2k，所以A(2,0)，B(0,- 2k)。故答案为(2,0)，(0,- 2k)。
(2)线段MN的长度不发生变化。因为一次函数y = kx - 2k的图象经过点(1,- 2)，所以 - 2 = k - 2k，所以k = 2，所以一次函数表达式为y = 2x - 4。因为平行于x轴的两条直线l₁，l₂分别与一次函数y = 2x - 4的图象交于点M，N，点M，N的横坐标分别为m，n，且m - n = 3，所以M(m,2m - 4)，N(n,2n - 4)，所以MN = $\sqrt{(m - n)² + (2m - 4 - 2n + 4)²}$ = $\sqrt{5(m - n)²}$ = $\sqrt{5×3²}$ = 3$\sqrt{5}$，所以当m - n = 3时，线段MN的长度不发生变化，为3$\sqrt{5}$。
(3)如图，因为y = kx - 2k = k(x - 2)，所以一次函数y = kx - 2k的图象过定点A(2,0)，所以OA = 2。设一次函数y = kx - 2k的图象与函数y = x图象的交点为P，点P的纵坐标为yₚ。当S△OAP = 1时，$\frac{1}{2}$OA·|yₚ| = 1即$\frac{1}{2}$×2|yₚ| = 1，解得yₚ = 1或yₚ = - 1。因为点P在函数y = x的图象上，所以点P的坐标为(1,1)或(- 1,- 1)。把(1,1)代入y = kx - 2k，解得k = - 1；把(- 1,- 1)代入y = kx - 2k解得k = $\frac{1}{3}$。结合图象可知，若一次函数y = kx - 2k的图象与函数y = x的图象及x轴所围成的三角形的面积不小于1，则k的取值范围是k ≤ - 1或k ≥ $\frac{1}{3}$且k≠1。