《2025年初中必刷题八年级数学上册北师大版》

1 [2025山东淄博期中,中]如图,点P为$Rt\triangle ABC$的边BC上一点,已知$PC= 5,AC= 10$,折线P-B-A与折线P-C-A的长度相等,则边BC的长为( )

A.6.5
B.7
C.7.5
D.8

答案： C　[解析]因为折线P−B−A与折线P−C−A 的长度相等,PC=5,AC=10,所以AC+PC=PB+AB=15.设PB=x,则AB=15−x,BC=5+x.在Rt△ABC中,AC²+BC²=AB²,即10²+(5+x)²=(15−x)²,解得x=2.5,所以BC=5+2.5=7.5.故选C.

2 [2025浙江杭州期中,中]如图,在$Rt\triangle ABC$中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为$S_{1},S_{2},S_{3}$,若$S_{3}+S_{2}-S_{1}= 24$,则图中阴影部分的面积为( )

A.6
B.12
C.10
D.8

答案： A　[解析]在Rt△ABC中,由勾股定理得AC²+AB²=BC²,则S₁+S₂=S₃.因为S₃+S₂−S₁=24,所以S₁+S₂+S₂−S₁=24,所以S₂=12.由题图易知，阴影部分的面积为$\frac{1}{2}$S₂=6.故选A.

3 [2025江苏无锡调研,中]如图,点A是射线BM外一点,连接AB,若$AB= 5cm$,点A到BM的距离为3cm,动点P从点B出发沿射线BM以2cm/s的速度运动.设运动的时间为ts,当$\triangle ABP$为直角三角形时,t的值为( )

A.$\frac {25}{4}$
B.2
C.2或$\frac {25}{4}$
D.2或$\frac {25}{8}$

答案：
D　[解析]过点A作AH⊥BM于H，因为点A到BM的距离为3cm，所以AH=3cm.因为AB=5cm，所以根据勾股定理，得BH²=AB²−AH²，所以BH=4cm.当∠APB=90°时，如图
(1)所示，此时点P与点H重合，则BP=BH=4cm，所以2t=4，解得t=2.当∠BAP=90°时，如图
(2)所示.因为AB=5cm，BP=2tcm，AH=3cm，BH=4cm，所以HP=(2t−4)cm.在Rt△BAP中，根据勾股定理，得AP²=BP²−AB²=4t²−25，在Rt△AHP中，根据勾股定理得AP²=AH²+HP²=9+(2t−4)²，所以4t²−25=9+(2t−4)²，解得t=$\frac{25}{8}$.综上所述，当△ABP为直角三角形时，t的值为2或$\frac{25}{8}$.故选D.
　 　　

4 [2025四川成都质检,中]如图,在$\triangle ABC$中,$∠ACB= 90^{\circ },AC= 3,BC= 4$,点D在边AB上,$AD= AC,AE⊥CD$,交BC,CD于点E,F,则BE的长是____.

答案：
$\frac{5}{2}$　[解析]连接DE,如图
因为AD=AC=3,AE⊥CD,所以AE是CD的垂直平分线，所以CE=DE，所以易得△ACE≌△ADE,所以∠ADE=∠ACB=90°.在Rt△ABC中,由勾股定理得AB²=AC²+BC²=25,所以AB=5,所以BD=AB−AD=2.因为S△ABC=S△ACE+S△ABE,AC×BC=AC×CE+AB×DE，所以3×4=3CE+5DE,所以DE=$\frac{3}{2}$.在Rt△BDE中,由勾股定理得BE²=DE²+BD²=($\frac{3}{2}$)²+2²=$\frac{25}{4}$,所以BE=$\frac{5}{2}$.故答案为$\frac{5}{2}$.
　　　　　　　　　　　　

5 [2025河南郑州质检,中]如图,在$\triangle ABC$中,$∠ACB= 90^{\circ },AC= 12,BC= 9$,射线CD与边AB交于点D.E,F分别为AD,BD的中点,设点E,F到射线CD的距离分别为m,n,则$m+n$的最大值为____.

答案：
7.5　[解析]如图，连接CE,CF,过E作CD的垂线,垂足为M,过F作CD的垂线，垂足为N,即EM=m,EN=n,所以S△CDF=$\frac{1}{2}$CD×n,S△CDE=$\frac{1}{2}$CD×m.因为E,F分别为AD,BD的中点,所以S△CDE=$\frac{1}{2}$S△CDA,S△CDF=$\frac{1}{2}$S△CDB,所以S△CEF=S△CDE+S△CDF=$\frac{1}{2}$(S△CDA+S△CDB),所以$\frac{1}{2}$CD(m+n)=$\frac{1}{2}$S△ABC.因为∠ACB=90°,所以S△ABC=$\frac{1}{2}$×9×12=54,所以$\frac{1}{2}$CD(m+n)=27,所以CD(m+n)=54,所以当CD最短时，m+n有最大值，此时CD⊥AB.因为在Rt△ABC中,由勾股定理得AB²=12²+9²=225,所以AB=15.设AB边上的高为h,所以$\frac{1}{2}$AB·h=54,所以h=7.2,即CD=7.2,所以m+n=$\frac{54}{7.2}$=7.5,所以m+n的最大值为7.5.故答案为7.5.
　　　　　　　　　　

6 [2025陕西西安质检,中]探究:
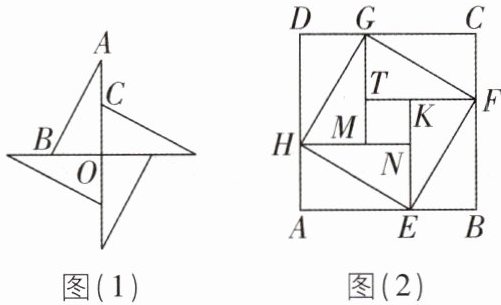
(1)图(1)是由四个全等的直角三角形紧密拼接形成的飞镖状图形,若$AB+AC= 20,OC= 5$,求该飞镖状图形的面积.
(2)图(2)是由八个全等的直角三角形紧密拼接形成的大正方形ABCD,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为$S_{1},S_{2},S_{3}$.若$S_{2}= 6$,求$S_{1}+S_{3}$的值.

答案： [解]
(1)由题意得OB=OC=5.因为AB+AC=20,OC=5,所以AB+(OA−5)=20,OA²+5²=AB²,所以AB=25−OA,所以OA²+5²=(25−OA)²,解得OA=12,所以该飞镖状图形的面积为4×$\frac{1}{2}$×12×5=120.
(2)设直角三角形的长直角边长为a,短直角边长为b,斜边长为c,则c²=a²+b².由题意得S₁=(a+b)²,S₂=c²=6,S₃=(a−b)²,所以S₁+S₂+S₃=(a+b)²+c²+(a−b)²=a²+2ab+b²+c²+a²−2ab+b²=c²+c²+c²=3c²=18,所以S₁+S₃=18−S₂=18−6=12.

7 [2025辽宁抚顺质检,较难]如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ }$,D为AB中点,点E在BC边上(点E不与点B,C重合),连接DE,过点D作$DF⊥DE$交AC于点F,连接EF.
(1)试说明:$AF^{2}+BE^{2}= EF^{2}$;
(2)若$AC= 7,BC= 5,EC= 1$,直接写出AF的长.

答案：
[解]
(1)延长ED至M使DM=DE,连接AM,FM,如图.因为D为AB中点，所以AD=BD.在△ADM与△BDE中，$\begin{cases}AD=BD,\\\angle ADM=\angle BDE,\\DM=DE,\end{cases}$所以△ADM≌△BDE(SAS),所以AM=BE,∠DAM=∠B,所以AM//BC,所以∠MAF=180°−∠C=90°.因为FD⊥ME,DE=DM,所以MF=FE.因为在Rt△MAF中,AM²+AF²=MF²,所以AF²+BE²=EF².
(2)AF=$\frac{17}{7}$.设AF=x.因为AC=7,BC=5,CE=1,所以CF=AC−AF=7−x,BE=BC−CE=4.因为∠C=90°,所以CF²+CE²=EF²,所以EF²=(7−x)²+1.由
(1)知MF=EF,∠MAF=90°,AM=BE,所以MF²=(7−x)²+1,AM=4.因为∠MAF=90°,所以AF²+AM²=MF²,所以x²+4²=(7−x)²+1,解得x=$\frac{17}{7}$,所以AF=$\frac{17}{7}$.