第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1 [2025 山东济南期中,中]如图(1)是某湖最深处的截面图,湖面下任意一点 A 的压强 P(单位:cmHg)与其深度 h(单位:m)的函数关系式为 P = ah + P₀,其图象如图(2)所示,其中 P₀ 为湖面大气压强,a 为常数且 a > 0,点 M 的坐标为(34.5,342).根据图中信息分析,下列结论正确的是( )

A.湖面大气压强为 76.0 cmHg
B.函数表达式 P = ah + P₀ 中 P 的取值范围是 P < 342
C.湖水深 20 m 处的压强为 256 cmHg
D.P 与 h 的函数表达式为 P = 8h + 66(0 ≤ h ≤ 34.5)

A.湖面大气压强为 76.0 cmHg
B.函数表达式 P = ah + P₀ 中 P 的取值范围是 P < 342
C.湖水深 20 m 处的压强为 256 cmHg
D.P 与 h 的函数表达式为 P = 8h + 66(0 ≤ h ≤ 34.5)
答案:
1.D 【解析】由图象可知,直线 P=ah+P₀ 过点(0,66)和(34.5,342),所以 P₀=66,34.5a+P₀=342,解得 P₀=66,a=8,所以函数表达式为 P=8h+66,所以湖面大气压强为 66 cmHg,故 D 选项正确,符合题意;A 选项错误,不符合题意. 根据实际意义可知,函数表达式 P=ah+P₀ 中 P 的取值范围是 66≤P≤342,故 B选项错误,不符合题意. 将 h=20 代入 P=8h+66,得 P=8×20+66=226,即湖水深 20 m 处的压强为 226 cmHg,故 C 选项错误,不符合题意. 故选 D.
2 [2025 四川资阳质检,中]已知关于 x 的方程 mx + 3 = 4 的解为 x = 1,则直线 y = (m - 2)x - 3 一定不经过第______象限.
答案:
2.一 【解析】因为关于 x 的方程 mx+3=4 的解为 x=1,所以 m+3=4,所以 m=1,所以直线 y=(m-2)x-3 可化为 y=-x-3. 因为 k=-1<0,b=-3<0,所以 y=-x-3 一定不经过第一象限,即直线 y=(m-2)x-3 一定不经过第一象限. 故答案为一.
3 [2025 四川成都期末,中]我国新能源汽车快速健康发展,续航里程不断提升.王师傅驾驶一辆纯电动汽车从一高速公路入口 A 驶入时,该车的剩余电量是 100 千瓦时,行驶了 360 千米后,从另一高速公路出口 B 驶出.已知该车在高速公路上行驶的过程中,剩余电量 y(千瓦时)与行驶路程 x(千米)之间的关系如图所示.
(1)求 y 关于 x 的函数表达式;
(2)若这辆车从高速公路入口 A 驶入时,剩余电量为 78 千瓦时,请问王师傅能在不充电的情况下行驶 360 千米到达高速公路出口 B 吗? 说明理由.
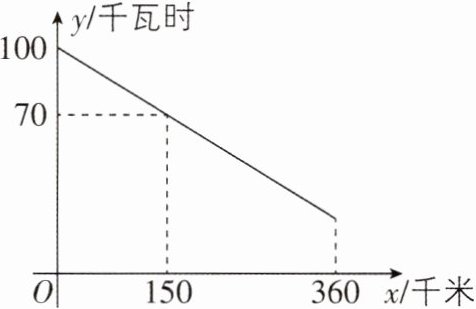
(1)求 y 关于 x 的函数表达式;
(2)若这辆车从高速公路入口 A 驶入时,剩余电量为 78 千瓦时,请问王师傅能在不充电的情况下行驶 360 千米到达高速公路出口 B 吗? 说明理由.

答案:
3.【解】
(1)设 y 关于 x 的函数表达式为 y=kx+b(k,b 为常数,且 k≠0). 将(0,100)和(150,70)分别代入 y=kx+b,得 b=100,①150k+b=70.②将①代入②,得 k=-$\frac{1}{5}$,所以 y 关于 x 的函数表达式为 y=-$\frac{1}{5}$x+100.
(2)王师傅能在不充电的情况下行驶 360 千米到达高速公路出口 B.
理由如下:
该纯电动汽车每千米消耗的电量为(100-70)÷150=$\frac{1}{5}$(千瓦时),该纯电动汽车从高速公路入口 A 行驶 360 千米消耗的电量为$\frac{1}{5}$×360=72(千瓦时).
因为 78>72,
所以王师傅能在不充电的情况下行驶 360 千米到达高速公路出口 B.
(1)设 y 关于 x 的函数表达式为 y=kx+b(k,b 为常数,且 k≠0). 将(0,100)和(150,70)分别代入 y=kx+b,得 b=100,①150k+b=70.②将①代入②,得 k=-$\frac{1}{5}$,所以 y 关于 x 的函数表达式为 y=-$\frac{1}{5}$x+100.
(2)王师傅能在不充电的情况下行驶 360 千米到达高速公路出口 B.
理由如下:
该纯电动汽车每千米消耗的电量为(100-70)÷150=$\frac{1}{5}$(千瓦时),该纯电动汽车从高速公路入口 A 行驶 360 千米消耗的电量为$\frac{1}{5}$×360=72(千瓦时).
因为 78>72,
所以王师傅能在不充电的情况下行驶 360 千米到达高速公路出口 B.
4 [2025 辽宁丹东质检,较难]某公司需要一批食品包装盒,有两种方案可供选择:
方案一:从包装盒加工厂直接购买,购买所需的费用$ y_1($元)与包装盒数 x(个)满足如图(1)所示的函数关系.
方案二:租赁机器自己加工,所需费用(包括租赁机器的费用和生产包装盒的费用$)y_2($元)与包装盒数 x(个)满足如图(2)所示的函数关系.
根据图象回答下列问题:
(1)方案一中包装盒的单价是多少?
(2)方案二中租赁机器的费用是多少? 生产的包装盒的单价是多少?
(3)请分别求出$ y_1,y_2 $关于 x 的函数表达式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?
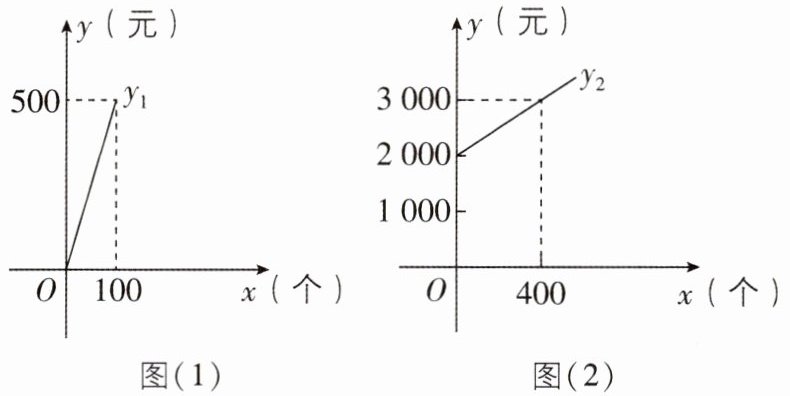
方案一:从包装盒加工厂直接购买,购买所需的费用$ y_1($元)与包装盒数 x(个)满足如图(1)所示的函数关系.
方案二:租赁机器自己加工,所需费用(包括租赁机器的费用和生产包装盒的费用$)y_2($元)与包装盒数 x(个)满足如图(2)所示的函数关系.
根据图象回答下列问题:
(1)方案一中包装盒的单价是多少?
(2)方案二中租赁机器的费用是多少? 生产的包装盒的单价是多少?
(3)请分别求出$ y_1,y_2 $关于 x 的函数表达式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?

答案:
4.【解】
(1)500÷100=5(元/个),所以方案一中包装盒 的单价为5元/个.
(2)根据题图
(2)可知,租赁机器 的费用为2000元,生产的包装盒的单价为(3000-2000)÷400=2.5(元/个).
(3)设y_{1}关于x的函数表达式为y_{1}=k_{1}x.
因为图象经过点(100,500),
所以500=100k_{1},
解得k_{1}=5,
所以y_{1}=5x.
设y_{2}关于x 的函数表达式为y_{2}=k_{2}x+b.因为图象经过点(0,2000)和(400,3000),
所以b=2000,400k_{2}+b=3000,
所以k_{2}=2.5,b=2000,
所以y_{2}=2.5x+2000.
(4)令5x=2.5x+2000,
解得x=800,
所以当x=800时,两种方案所需费用一样;
当$0\lt x\lt800$时,选择方案一更省钱;
当$x\gt800$时 ,选择方案二更省钱 .
(1)500÷100=5(元/个),所以方案一中包装盒 的单价为5元/个.
(2)根据题图
(2)可知,租赁机器 的费用为2000元,生产的包装盒的单价为(3000-2000)÷400=2.5(元/个).
(3)设y_{1}关于x的函数表达式为y_{1}=k_{1}x.
因为图象经过点(100,500),
所以500=100k_{1},
解得k_{1}=5,
所以y_{1}=5x.
设y_{2}关于x 的函数表达式为y_{2}=k_{2}x+b.因为图象经过点(0,2000)和(400,3000),
所以b=2000,400k_{2}+b=3000,
所以k_{2}=2.5,b=2000,
所以y_{2}=2.5x+2000.
(4)令5x=2.5x+2000,
解得x=800,
所以当x=800时,两种方案所需费用一样;
当$0\lt x\lt800$时,选择方案一更省钱;
当$x\gt800$时 ,选择方案二更省钱 .
查看更多完整答案,请扫码查看


