《2025年初中必刷题八年级数学上册北师大版》

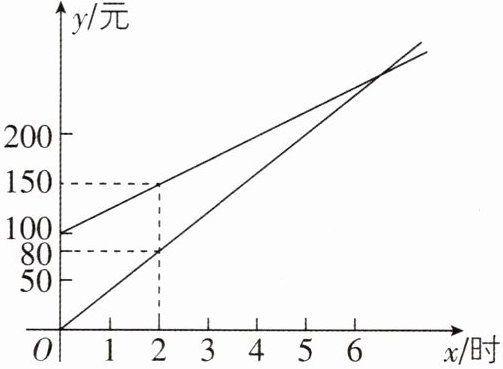
10 [2025山东烟台期末]某羽毛球馆有两种收费方式：$A$种是办理会员卡后每小时按优惠价付费,但需按月缴纳一定的会员费；$B$种是不办会员卡直接按打球时间付费,两种收费方式每月的收费情况如图所示,根据图中提供的信息解答下列问题.
(1)$A$种方式要求客户每月支付的会员费是______元,$B$种方式每小时打球收费______元；
(2)求出$A种方式的月费用y$(元)与打球时间$x$(时)之间的函数关系式；
(3)小王每月打球时间为10小时,他选用哪种收费方式更合算？

答案： 10.[解]
(1)由题图可知,A种方式要求客户每月支付的会员费是100元，B种方式每小时打球收费80÷2=40(元).故答案为100,40.
(2)设y与x之间的函数关系式为y=kx+b,将(0,100),(2,150)代入,得b=100,2k+b=150,解得b=100,k=25,所以y=25x+100.
(3)当x=10时,A种方式需付费25×10+100=350(元),B种方式需付费40×10=400(元).因为350＜400,所以他选用A种收费方式更合算.

11 新考法 [2025福建宁德期中]某数学兴趣小组以“钟表上时针和分针的重合次数”为课题进行研究. 研究发现：时针每分转$0.5$度,分针每分转6度,并且从某时刻开始,经过的时间与时针和分针的重合次数存在一定的关系. 如图是某钟表的简化平面示意图,此刻时间恰好为$1:00$.

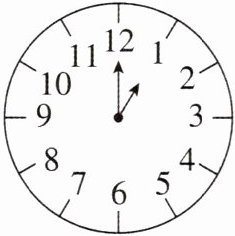
(1)此刻分针和时针的夹角为______度；
(2)兴趣小组为了研究经过的时间与时针和分针重合次数之间的关系,制作如下表格,其中$x$(次)表示从$1:00$开始,时针和分针重合的次数,$y$(分)表示从$1:00$开始经过的时间,请将表格填写完整.
| $x/$次 | 1 | 2 | 3 | …$$ |
| $y/$分 | $\frac{60}{11}$ | ______ | ______ | …$$ |
(3)直接写出$y与x$之间的函数关系式,并求从$1:00$开始经过24时时,分针和时针重合的次数.

答案： 11.[解]
(1)分针和时针的夹角为360°÷12=30°.故答案为30.
(2)设从1:00开始，经过a分时针和分针第2次相遇,则6a−0.5a=360+30,解得$a=\frac{780}{11}$.设从1:00开始，经过b分时针和分针第3次相遇,则6b−0.5b=360×2+30,解得$b=\frac{1500}{11}$.表格如下:
x/次 1 2 3 …
y/分 $\frac{60}{11}$ $\frac{780}{11}$ $\frac{1500}{11}$ …
故答案为$\frac{780}{11}$,$\frac{1500}{11}$.
(3)$y=\frac{720}{11}x-60$(x是正整数).由
(2)易知,从第一次重合后，每隔$\frac{720}{11}$分，时针与分针再次重合,所以$y=\frac{720}{11}(x-1)+\frac{60}{11}=\frac{720}{11}x-60$(x是正整数).24时=1440分,当y=1440时,$\frac{720}{11}x-60=1440$,所以$x=\frac{275}{12}=22\frac{11}{12}$.因为x是正整数,所以x=22.
答:从1:00开始经过24时时，分针和时针重合的次数为22次

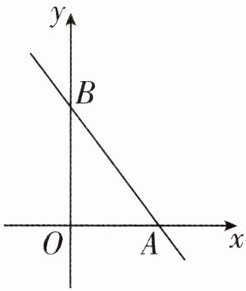
12 如图,在平面直角坐标系中,已知一次函数$y = - \frac{4}{3}x + 4的图象分别与x$轴、$y轴交于点A$,$B$.
(1)点$A$的坐标是______,点$B$的坐标是______.
(2)若点$C(m,6)是直线y = - \frac{4}{3}x + 4$上一点,则直线$OC$的表达式是______.
(3)在直线$AB上是否存在一点D$(不与点$B$重合),使$\triangle AOD的面积等于\triangle OAB$的面积？若存在,求出点$D$的坐标；若不存在,请说明理由.
(4)点$E是y$轴上一动点,把线段$AB沿着直线AE$翻折,使点$B落在x$轴上,请直接写出折痕所在直线的表达式.

答案：
12.[解]
(1)令x=0,则y=4,所以B(0,4).令y=0,则x=3,所以A(3,0).故答案为(3,0),(0,4).
(2)将点C(m,6)代入$y=-\frac{4}{3}x+4$,得$-\frac{4}{3}m+4=6$,解得$m=-\frac{3}{2}$,所以$C(-\frac{3}{2},6)$.设直线OC的表达式为y=kx(k≠0),则$-\frac{3}{2}k=6$,解得k=−4,所以y=−4x.故答案为y=−4x.
(3)直线AB上存在点D,使△AOD的面积等于△OAB的面积.设$D(t,-\frac{4}{3}t+4)$,所以$S_{\triangle AOD}=\frac{1}{2}×3×|-\frac{4}{3}t+4|$,$S_{\triangle OAB}=\frac{1}{2}×3×4=6$.因为△AOD的面积等于△OAB的面积,所以$\frac{1}{2}×3×|-\frac{4}{3}t+4|=6$,解得t=0(舍去)或t=6,所以D(6,−4).
(4)$y=-\frac{1}{2}x+\frac{3}{2}$或y=2x−6.
设E(0,n).如图
(1),当B点的对应点B₁在x轴负半轴上时,由翻折可知BE=B₁E=4−n,$AB=AB₁=\sqrt{3^{2}+4^{2}}=5$.因为OA=3,所以OB₁=2.在Rt△B₁EO中,(4−n)²=4+n²,解得$n=\frac{3}{2}$,所以$E(0,\frac{3}{2})$,所以直线AE的表达式为$y=-\frac{1}{2}x+\frac{3}{2}$.如图
(2),当B点的对应点B₂在x轴正半轴上时,由翻折可知,BE=B₂E=4−n,AB=AB₂=5,所以OB₂=8.在Rt△OEB₂中,(4−n)²=n²+64,解得n=−6,所以E(0,−6),所以直线AE的表达式为y=2x−6.综上所述,折痕所在直线的表达式为$y=-\frac{1}{2}x+\frac{3}{2}$或y=2x−6.