《2025年初中必刷题八年级数学上册北师大版》

1 [2025陕西渭南期末,中]小明走楼梯回家,他所走的台阶总数$ m $(个)是楼层的层数$ n $(层)($ n \geq 2 且 n $为整数)的一次函数,其部分对应值如表所示：
| 层数$ n / $层 | 2 | 3 | 4 | 5 | …$ $ |
| 台阶总数$ m / $个 | 42 | 70 | 98 | 126 | …$ $ |
当层数为20层时,小明走的台阶总数为( )

A.560个
B.546个
C.574个
D.592个

答案： B 【解析】设一次函数表达式为 m=kn+b. 将(2,42),(3,70)代入得{2k+b=42,3k+b=70,解得{k=28,b=-14,所以 m=28n-14. 当 n=20 时,m=28×20-14=546. 故选 B.

2 [中]已知直线$ l _ { 1 } 与 x 轴交于点 A ( - 2 , 0 ) $,与$ y $轴交于正半轴,且直线$ l _ { 1 } $与两坐标轴围成的三角形的面积为4. 将直线$ l _ { 1 } 向下平移 m ( m ＞ 0 ) 个单位得到直线 l _ { 2 } $,直线$ l _ { 2 } 交 x 轴于点 B $,若点$ A 与点 B 关于 y $轴对称,则$ m $的值为( )

A.8
B.7
C.6
D.5

答案：
A 【解析】根据题意,画出示意图如图. 设直线 l₁与 y 轴交于点 C,点 C 的坐标为(0,n)(n＞0),直线 l₂与 y 轴交于点 D. 因为点 A 与点 B 关于 y 轴对称,所以点 B 的坐标为(2,0). 因为直线 l₁与两坐标轴围成的三角形的面积为 4,点 A(-2,0),所以$\frac{1}{2}$×|-2|×n=4,解得 n=4,所以点 C 的坐标为(0,4). 设直线 l₁的表达式为 y=kx+b. 把 A(-2,0),C(0,4)代入,得{-2k+b=0,b=4,解得{k=2,b=4,所以 y=2x+4. 因为直线 l₂由直线 l₁平移得到,所以设直线 l₂的表达式为 y=2x+b'. 把 B(2,0)代入,得 2×2+b'=0,解得 b'=-4,所以直线 l₂的表达式为 y=2x-4,所以点 D 的坐标为(0,-4),所以 m=4-(-4)=8. 故选 A.

3 [2025福建厦门期末,中]某校科技节上,同学们在操场进行无人机表演,其中甲、乙两架无人机离操场地面的高度$ y $(单位：米)与表演时间$ x $(单位：秒)的图象如图所示. 已知表演开始时甲、乙离地的高度分别是5米、15米,在1分钟的表演过程中甲、乙两架无人机的高度差不超过5米的时间可持续____秒.

答案： 20 【解析】设 y甲=k₁x+b₁,将(0,5),(20,60)分别代入,得{5=b₁,60=20k₁+b₁,解得{k₁=2.75,b₁=5,则 y甲=2.75x+5. 设 y乙=k₂x+b₂,将(0,15),(20,60)分别代入,得{15=b₂,60=20k₂+b₂,解得{k₂=2.25,b₂=15,则 y乙=2.25x+15. 当 x＜20 时,y乙-y甲=5,即2.25x+15-2.75x-5=5,解得 x=10;当 x＞20 时,y乙-y甲=-5,即2.25x+15-2.75x-5=-5,解得 x=30. 30-10=20(秒). 故答案为 20.

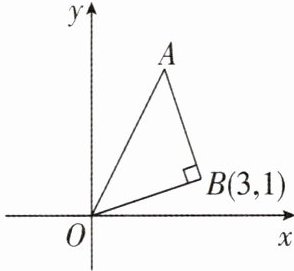
4 [2025辽宁辽阳期末,中]如图,在平面直角坐标系中,点$ B 的坐标为 ( 3 , 1 ) $,$ A B = O B $,$ \angle A B O = 90 ^ { \circ } $,则直线$ A B $的函数表达式是____.

答案：
y=-3x+10 【解析】如图,过点 A 作 AC//x 轴交 y 轴于点 C,过点 B 作 BD//y 轴交 x 轴于点 D,两条直线相交于点 E,易得∠ACO=∠E=∠BDO=90°,所以∠BAE+∠EBA=90°. 因为∠ABO=90°,所以∠EBA+∠OBD=90°,所以∠OBD=∠BAE. 因为 B(3,1),所以 OD=3,BD=1. 在△ABE 与△BOD 中,{∠AEB=∠ODB=90°,∠BAE=∠OBD,AB=OB,所以△ABE≌△BOD(AAS),所以 AE=BD=1,BE=OD=3,所以 AC=CE-AE=OD-AE=2,DE=BD+BE=4,所以 A(2,4). 设直线 AB 的表达式为 y=kx+b. 将 A(2,4),B(3,1)代入,得{2k+b=4,3k+b=1,解得{k=-3,b=10,所以直线 AB 的表达式为 y=-3x+10. 故答案为 y=-3x+10.

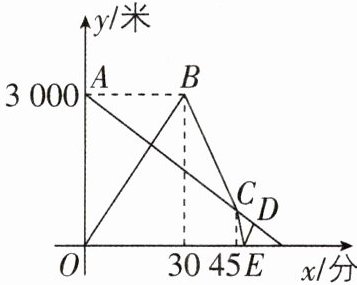
5 [中]小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,两人一同回家. 如图是两人离家的距离$ y $(米)与小明出发的时间$ x $(分)之间的函数图象.
(注：小明和妈妈始终在同一条笔直的公路上行走,图象上$ A $,$ C $,$ D $三点在一条直线上)
(1)求线段$ B C $的函数表达式；
(2)求点$ D $的坐标,并说明点$ D $的实际意义.

答案：
(1)因为 45×50=2250(米),3000-2250=750(米),所以点 C 的坐标为(45,750). 设线段 BC 的函数表达式为 y=kx+b(k≠0,30≤x≤45).把(30,3000),(45,750)代入 y=kx+b,得{30k+b=3000,45k+b=750,解得{k=-150,b=7500.所以线段 BC 的函数表达式为 y=-150x+7500(30≤x≤45).
(2)设 AC 所在直线的函数表达式为 y=k₁x+b₁.把(0,3000),(45,750)代入 y=k₁x+b₁,得{b₁=3000,45k₁+b₁=750,解得{k₁=-50,b₁=3000.所以 AC 所在直线的函数表达式为 y=-50x+3000.因为 750÷250=3(分),45+3=48(分),所以点 E 的坐标为(48,0).所以易得 ED 所在直线的函数表达式为 y=250(x-48)=250x-12000.联立,得方程组{y=-50x+3000,y=250x-12000,解得{x=50,y=500,所以点 D 的坐标为(50,500).点 D 的实际意义:小明将在出发 50 分时离家 500 米的地方接到妈妈.

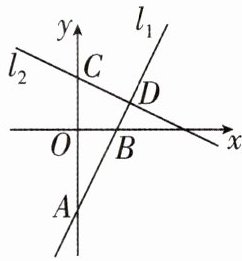
6 [2024山东淄博期末,较难]如图,直线$ l _ { 1 } : y _ { 1 } = k x + b 与 y 轴交于点 A $,与$ x 轴交于点 B \left( \dfrac { 3 } { 2 } , 0 \right) $,直线$ l _ { 2 } : y _ { 2 } = - \dfrac { 1 } { 2 } x + 2 与 y 轴交于点 C $,与直线$ l _ { 1 } 交于点 D $,点$ D 到 y $轴的距离为2.
(1)求直线$ l _ { 1 } $的函数表达式.
(2)请直接写出方程组$ \left\{ \begin{array} { l } { k x - y = - b , } \\ { x + 2 y = 4 } \end{array} \right. $的解：____.
(3)求$ \triangle A C D $的面积.
(4)在直线$ l _ { 1 } 上是否存在异于点 D 的另一点 M $,使得$ \triangle A C D 与 \triangle A C M $的面积相等？若存在,请求出点$ M $的坐标；若不存在,请说明理由.

答案：
(1)因为点 D 到 y 轴的距离为 2,所以点 D 的横坐标为 2. 把 x=2 代入 y₂=-$\frac{1}{2}$x+2,得 y₂=-$\frac{1}{2}$×2+2=1,所以 D(2,1). 把 B($\frac{3}{2}$,0),D(2,1)代入 y₁=kx+b,得{$\frac{3}{2}$k+b=0,2k+b=1,解得{k=2,b=-3,所以直线 l₁的函数表达式为 y₁=2x-3.
(2)根据原方程组易知,直线 l₁与直线 l₂交点的坐标即为原方程组的解. 因为直线 l₁:y₁=2x-3 与直线 l₂:y₂=-$\frac{1}{2}$x+2 交于点 D(２,1),所以方程组{2x-y=3,x+2y=4 的解是{x=2,y=1,故答案为{x=2,y=1.
(3)把 x=0 代入 y₂=-$\frac{1}{2}$x+2,得 y₂=2,所以 C(0,2). 把 x=0 代入 y₁=2x-3,得 y₁=-3,所以 A(0,-3),所以 AC=2+3=5,所以 S△ACD=$\frac{1}{2}$×5×2=5.
(4)存在,M(-2,-7). 若在直线 l₁上存在异于点 D 的另一点 M,使得△ACD 与△ACM 的面积相等,则点 M 到 y 轴的距离为 2,所以点 M 的横坐标为-2,把 x=-2 代入 y₁=2x-3,得 y₁=2×(-2)-3=-7,所以 M 点的坐标为(-2,-7).