《2025年初中必刷题八年级数学上册北师大版》

1[2025四川成都期中]下列说法中,正确的是( )

A.27的立方根是3,记作$\sqrt {27}= 3$
B.-25的算术平方根是5
C.a的三次方根是$\pm \sqrt [3]{a}$
D.0的立方根是0

答案： D 【解析】27 的立方根是 3，记作$\sqrt [3]{27}=3$，故 A 选项错误，不符合题意；-25 是负数，负数没有算术平方根，故 B 选项错误，不符合题意；a 的三次方根是$\sqrt [3]{a}$，故 C 选项错误，不符合题意；0 的立方根是 0，故 D 选项正确，符合题意. 故选 D.

2[2025湖南衡阳期中]关于立方根,下列说法正确的是( )

A.正数有两个立方根
B.立方根等于它本身的数只有0
C.负数的立方根是负数
D.负数没有立方根

答案： C 【解析】正数有一个立方根，故 A 选项错误，不符合题意；立方根等于它本身的数有-1，0，1，故 B 选项错误，不符合题意；负数的立方根是负数，故 C 选项正确，符合题意；负数有立方根，故 D 选项错误，不符合题意. 故选 C.

3[2023浙江嘉兴中考]-8的立方根是( )

A.-2
B.2
C.±2
D.不存在

答案： A 【解析】-8 的立方根是$\sqrt [3]{-8}$，即$\sqrt [3]{(-2)^{3}}=-2$，故选 A.

4[2025甘肃张掖质检]下列计算正确的是( )

A.$\sqrt [3]{(-2)^{3}}= 2$
B.$\sqrt [3]{-0.064}= -0.4$
C.$(\sqrt [3]{-21})^{3}= 21$
D.$\sqrt [3]{-\frac {27}{64}}= \pm \frac {3}{4}$

答案： B 【解析】$\sqrt [3]{(-2)^{3}}=-2$，故 A 选项错误，不符合题意；$\sqrt [3]{-0.064}=-0.4$，故 B 选项正确，符合题意；$(\sqrt [3]{-21})^{3}=-21$，故 C 选项错误，不符合题意；$\sqrt [3]{-\frac {27}{64}}=-\frac {3}{4}$，故 D 选项错误，不符合题意. 故选 B.

5[2025山东烟台期末]已知$\sqrt [3]{a+2}= -2$,则a的值为____.

答案： -10 【解析】因为$\sqrt [3]{a+2}=-2$，所以$a+2=(-2)^{3}=-8$，解得$a=-10$. 故答案为-10.

6[2024安徽淮南期中]一个正数b的平方根为a+1和2a-7,则9a+b的立方根是( )

A.2
B.3
C.9
D.±3

答案： B 【解析】因为正数 b 的平方根为$a+1$和$2a-7$，所以$a+1+2a-7=0$，所以$a=2$，所以$a+1=2+1=3$，所以$b=3^{2}=9$，所以$9a+b=9×2+9=27$，所以$9a+b$的立方根是 3，故选 B.

7[2025陕西榆林期中]如果x是125的立方根,那么x的算术平方根是( )

A.25
B.$\sqrt {5}$
C.5
D.±5

答案： B 【解析】因为$\sqrt [3]{125}=5$，所以$x=5$. 因为 5 的算术平方根是$\sqrt {5}$，所以 x 的算术平方根是$\sqrt {5}$，故选 B.

8[2025福建三明期中]如图,数轴上表示$\sqrt [3]{-27}+\sqrt {9}$的点一定在( )


A.第①段
B.第②段
C.第③段
D.第④段

答案： B【解析】因为$\sqrt [3]{-27}+\sqrt {9}=-3+3=0$，所以数轴上表示$\sqrt [3]{-27}+\sqrt {9}$的点一定在第②段. 故选 B.

9[2024河南鹤壁期末]小明是一个电脑爱好者,他设计了一个程序,如图,当输入的x值是64时,输出的y值是____.

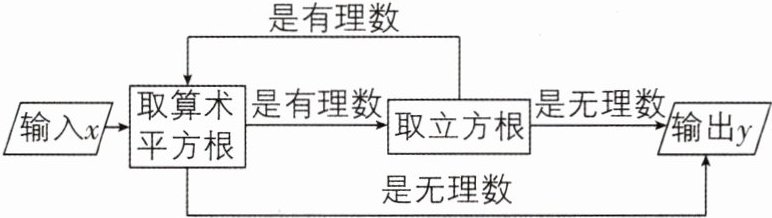
答案： $\sqrt {2}$【解析】当 x 为 64 时，取算术平方根得 8，8 取立方根得 2，2 取算术平方根得$\sqrt {2}$，$\sqrt {2}$是无理数，所以输出的 y 值为$\sqrt {2}$. 故答案为$\sqrt {2}$.

10[2025广东佛山质检]已知a+1的算术平方根是1,-27的立方根是b-12,c-3的平方根是±2.
(1)求a,b,c的值;
(2)求a+b+c的平方根和立方根.

答案： 【解】
(1)因为$a+1$的算术平方根是1，所以$a+1=1$，解得$a=0$. 因为-27的立方根是$b-12$，所以$b-12=-3$，所以$b=9$. 因为$c-3$的平方根是±2，所以$c-3=4$，所以$c=7$.
(2)由
(1)知，$a=0$，$b=9$，$c=7$，所以$a+b+c=0+9+7=16$，所以$a+b+c$的平方根是±4，$a+b+c$的立方根是$\sqrt [3]{16}$.

11[2025河南南阳调研]每年农历八月十五是我国的传统节日中秋节,自古便有中秋节赏月品月饼的习俗.某商店的李师傅制作的正方体月饼礼盒的体积为$216cm^3,$而王师傅制作的正方体月饼礼盒的体积比李师傅制作的小$91cm^3,$则王师傅制作的正方体月饼礼盒的表面积为____.

答案： $150cm^{2}$【解析】根据题意，得$\sqrt [3]{216-91}=\sqrt [3]{125}=5(cm)$，即王师傅制作的正方体月饼礼盒的棱长为 5 cm，则其表面积为$5×5×6=150(cm^{2})$. 故答案为$150cm^{2}$.

12当a取____时,$\sqrt [3]{3-a}$有意义.

答案： 任意实数 【解析】由于任意实数都有立方根，所以$3-a$为任意实数，即 a 为任意实数，故答案为任意实数.