《2025年初中必刷题八年级数学上册北师大版》

1[2023山东日照中考]已知直角三角形的三边a,b,c满足c＞a＞b,分别以a,b,c为边作三个正方形,把两个较小的正方形放置在最大正方形内,如图,设三个正方形无重叠部分的面积为$S_1,$均重叠部分的面积为$S_2,$则 ( )
$A.S_1＞S_2 B.S_1＜S_2 C.S_1= S_2 D.S_1,S_2$大小无法确定

答案： C 【解析】因为直角三角形的三边a,b,c满足c＞a＞b,所以该直角三角形的斜边为c,所以$c^{2}=a^{2}+b^{2}$,所以$c^{2}-a^{2}-b^{2}=0$,所以$S_{1}=c^{2}-a^{2}-b^{2}+b(a+b-c)=ab+b^{2}-bc$.因为$S_{2}=b(a+b-c)=ab+b^{2}-bc$,所以$S_{1}=S_{2}$,故选C.

2[2023江苏扬州中考]如图,△ABC中,∠A= 90°,AB= 8,AC= 15,以点B为圆心,适当长为半径画弧,分别交BA,BC于点M,N,再分别以点M,N为圆心,大于1/2MN的长为半径画弧,两弧交于点E,作射线BE交AC于点D,则线段AD的长为______.

答案：
$\frac{24}{5}$【解析】如图,过点D作$DH\perp BC$于点H.由题意可得,BE为$\angle ABC$的平分线.在$\triangle ABC$中,$\angle A=90^{\circ}$,$AB=8$,$AC=15$,所以$BC^{2}=AB^{2}+AC^{2}=8^{2}+15^{2}=289$,所以$BC=17$.因为BE平分$\angle ABC$,$DA\perp AB$,$DH\perp BC$,所以$DA=DH$.因为$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle DCB}$,所以$\frac{1}{2}×8×15=\frac{1}{2}×8× AD+\frac{1}{2}×17× DH$,所以$AD=DH=\frac{24}{5}$.故答案为$\frac{24}{5}$.

3[2024江苏常州中考]如图,在Rt△ABC中,∠ACB= 90°,AC= 6,BC= 4,D是边AC的中点,E是边BC上一点,连接BD,DE.将△CDE沿DE翻折,点C落在BD上的点F处,则CE= ______.

答案： $\frac{3}{2}$【解析】因为$\angle ACB=90^{\circ}$,$AC=6$,$BC=4$,D是边AC的中点,所以$CD=\frac{1}{2}AC=3$,所以$BD^{2}=BC^{2}+CD^{2}=25$,所以$BD=5$.因为将$\triangle CDE$沿DE翻折,点C落在BD上的点F处,所以$CD=DF=3$,$CE=EF$,$\angle EFD=\angle ACB=90^{\circ}$,所以$BF=BD-DF=2$,$\angle BFE=90^{\circ}$.设$CE=x$,则$EF=x$,$BE=BC-CE=4-x$.在$Rt\triangle BFE$中,由勾股定理,得$(4-x)^{2}=x^{2}+2^{2}$,解得$x=\frac{3}{2}$,所以$CE=\frac{3}{2}$.故答案为$\frac{3}{2}$.

4[2024黑龙江大庆中考]如图(1),直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图(2)是1次操作后的图形.图(3)是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图(1)中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为______.

答案：
48【解析】如图.因为$\angle ACB=90^{\circ}$,根据勾股定理,得$AC^{2}+BC^{2}=AB^{2}=2^{2}=4$,所以题图
(1)中所有正方形的面积和为4+4=8,题图
(2)中所有正方形的面积和,即1次操作后图形中所有正方形的面积和为8+4=12,2次操作后图形中所有正方形的面积和为8+4×2=16,3次操作后图形中所有正方形的面积和为8+4×3=20,…,所以n次操作后图形中所有正方形的面积和为8+4n,所以10次操作后图形中所有正方形的面积和为8+4×10=48.

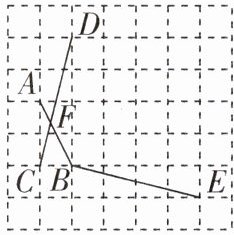
5[2023山东济宁中考]如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点A,B,C,D,E均在小正方形方格的顶点上,线段AB,CD交于点F,若∠CFB= α,则∠ABE等于 ( )

A.180°-α
B.180°-2α
C.90°+α
D.90°+2α

答案：
C 【解析】如图,过B点作$BG// CD$,连接EG.因为$BG// CD$,所以$\angle ABG=\angle CFB=\alpha$.因为$BG^{2}=1^{2}+4^{2}=17$,$BE^{2}=1^{2}+4^{2}=17$,$EG^{2}=3^{2}+5^{2}=34$,所以$BG^{2}+BE^{2}=EG^{2}$,所以$\triangle BEG$是直角三角形,所以$\angle GBE=90^{\circ}$,所以$\angle ABE=\angle GBE+\angle ABG=90^{\circ}+\alpha$.故选C.

6[湖北黄冈中考]勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,径隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是______(结果用含m的式子表示).

答案： $m^{2}+1$【解析】因为m为正整数,所以2m为偶数.设其股是a,则弦为a+2.根据勾股定理得$(2m)^{2}+a^{2}=(a+2)^{2}$,解得$a=m^{2}-1$,所以弦是$a+2=m^{2}-1+2=m^{2}+1$,故答案为$m^{2}+1$.

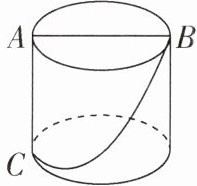
7[浙江金华中考]如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是 ( )

答案： C 【解析】将圆柱侧面沿AC“剪开”,侧面展开图为长方形,由题意知圆柱的底面直径为AB,且点B是展开图的一边的中点,蚂蚁爬行的最近路线为线段,则C选项符合题意,故选C.