《2025年初中必刷题八年级数学上册北师大版》

一、选择题(本大题共5小题,每小题5分,共25分)
1 对于一次函数$y = - x + 5$,下列结论正确的是 ( )

A.函数的图象不经过第三象限
B.函数的图象与$x轴的交点坐标是(2,0)$
C.函数的图象向下平移4个单位长度后得到$y = - 2x$的图象
D.若两点$A(1,y_{1})$,$B(3,y_{2})$在该函数图象上,则$y_{1} ＜ y_{2}$

答案： 1.A　[解析]因为k=−1,b=5,所以函数的图象经过第一、二、四象限，不经过第三象限，故A选项正确;当y=0时,−x+5=0,解得x=5,故函数的图象与x轴的交点坐标是(5,0),故B选项错误;一次函数y=−x+5的图象向下平移4个单位长度后得到y=−x+1的图象,故C选项错误;若两点A(1,y₁),B(3,y₂)在该函数图象上,1＜3,则y₁＞y₂,故D选项错误.故选A.

2 李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程$y$(千米)与行驶的时间$t$(时)的函数关系的大致图象是 ( )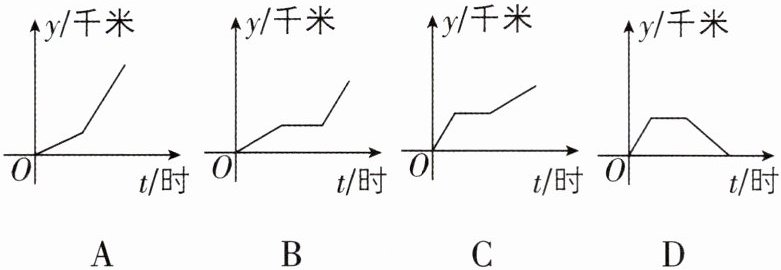

答案： 2.B　[解析]随着时间的增多，行进的路程也将增多，故D选项错误;由于途中停车加油耽误了几分，此时时间在增多，而路程没有变化，故A选项错误;后来加快了速度，仍保持匀速行驶，所以后来的函数图象应比前面匀速行驶的图象要陡，故B选项正确.故选B.

3 [2024广西贵港港北区期末]两个一次函数$y_{1} = ax + b与y_{2} = bx + a$在同一直角坐标系中的图象可能是 ( )

答案： 3.C　[解析]A选项，因为一次函数y₁=ax+b的图象经过第一、三、四象限，所以a＞0,b＜0,而由一次函数y₂=bx+a的图象可知,b＜0,a＜0,矛盾，故本选项错误;B选项，因为一次函数y₁=ax+b的图象经过第一、二、三象限,所以a＞0,b＞0,而由一次函数y₂=bx+a的图象可知,a＞0,b＜0,矛盾，故本选项错误;C选项，因为一次函数y₁=ax+b的图象经过第一、三、四象限,所以a＞0,b＜0,而由一次函数y₂=bx+a的图象可知,a＞0,b＜0,故本选项正确;D选项，因为一次函数y₁=ax+b的图象经过第一、二、四象限，所以a＜0,b＞0,而由一次函数y₂=bx+a的图象可知,a＜0,b＜0,矛盾，故本选项错误.故选C.

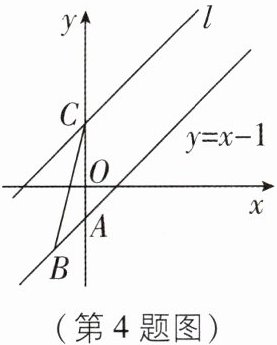
4 [2025内蒙古包头校级期中]如图,直线$y = x - 1与y轴交于点A$,点$B(b,-2)在直线y = x - 1$上.将直线$y = x - 1向上平移m个单位长度得到直线l$,直线$l与y轴交于点C$,若$\triangle ABC的面积为\frac{3}{2}$,则$m$的值为 ( )

A.2
B.3
C.6
D.4

答案： 4.B　[解析]因为点B(b,−2)在直线y=x−1上,所以b−1=−2,解得b=−1,所以点B(−1,−2).由平移知AC=m,所以$S_{\triangle ABC}=\frac{1}{2}×1×m=\frac{3}{2}$,所以m=3.故选B.

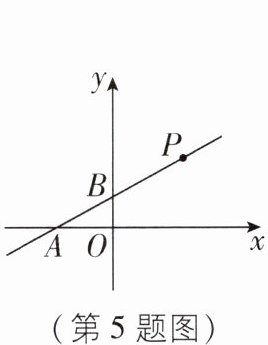
5 如图,直线$l:y = \frac{1}{2}x + m交x轴于点A$,交$y轴于点B(0,1)$,点$P(n,2)在直线l$上,已知$M是x$轴上的动点. 当以$A$,$P$,$M$为顶点的三角形是直角三角形时,点$M$的坐标为 ( )

A.$(-2,0)或(3,0)$
B.$(2,0)或(3,0)$
C.$(1,0)或(4,0)$
D.$(2,0)或(4,0)$

答案：
5.B
思路分析 直角三角形的分类讨论
以A,P,M为顶点的三角形是直角三角形 M在x轴上 ∠AMP=90°,∠APM=90°
[解析]因为直线l:$y=\frac{1}{2}x+m$交y轴于点B(0,1),所以$1=\frac{1}{2}×0+m$,解得m=1,则直线l的表达式为$y=\frac{1}{2}x+1$.当y=0时,$\frac{1}{2}x+1=0$,解得x=−2,所以点A的坐标为(−2,0).当y=2时,$\frac{1}{2}n+1=2$,解得n=2,所以点P的坐标为(2,2).如图,分两种情况考虑:
①当∠AMP=90°时,
　　　　　　　　　　
PM⊥x轴,则点M的坐标为(2,0).
②当∠APM′=90°时,设点M′的坐标为(a,0),则$AP^{2}=[2-(-2)]^{2}+(2-0)^{2}=20$,$AM'^{2}=[a-(-2)]^{2}=a^{2}+4a+4$,$PM'^{2}=(2-a)^{2}+(2-0)^{2}=a^{2}-4a+8$.因为$AP^{2}+PM'^{2}=AM'^{2}$,所以20+a²−4a+8=a²+4a+4,解得a=3,所以点M′的坐标为(3,0).综上所述，点M的坐标为(2,0)或(3,0).故选B.

二、填空题(本大题共4小题,每小题5分,共20分)
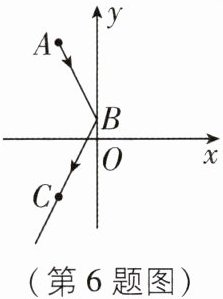
6 新考向 跨学科综合 [2025江西景德镇期末]如图,一束光线从点$A(-2,5)$出发,经过$y轴上的点B(0,1)反射后经过点C(m,n)$,则$2m - n$的值是______.

答案： 6.−1　[解析]设点A(−2,5)关于y轴的对称点为A′(2,5),所以反射光线所在直线过点B(0,1)和A′(2,5).设反射光线所在直线的表达式为y=kx+1,将A′(2,5)代入,得5=2k+1,所以k=2,所以反射光线所在直线的表达式为y=2x+1.因为光线反射后经过点C(m,n),所以2m+1=n,所以2m−n=−1.故答案为−1.

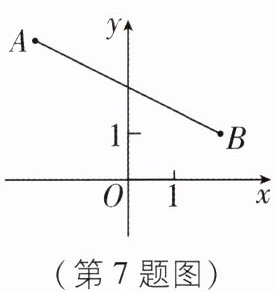
7 [2024河北石家庄新华区质检]如图,已知点$A(-2,3)$,$B(2,1)$,当直线$y = kx - k与线段AB$有交点时,$k$的取值范围是______.

答案： 7.k≤−1或k≥1　[解析]因为y=kx−k=k(x−1),所以直线y=kx−k恒过点(1,0).当直线刚好过点A时,将A(−2,3)代入y=kx−k中得3=−2k−k,解得k=−1.当直线刚好过点B时,将B(2,1)代入y=kx−k中得1=2k−k,解得k=1,所以当直线y=kx−k与线段AB有交点时,k的取值范围为k≤−1或k≥1,故答案为k≤−1或k≥1.

8 [2024四川绵阳涪城区期末]已知函数$y = \vert x - 2a\vert$($a$为常数),当$1 \leq x \leq 3$时,$y$的最小值为5,则$a$的值为______.

答案： 8.−2或4　[解析]分两种情况讨论:①当x≥2a时,y=x−2a.因为k=1＞0,所以当1≤x≤3时,y随x的增大而增大,即当x=1时,y=5,则5=1−2a,解得a=−2.②当x＜2a时,y=−x+2a.因为k=−1＜0,所以当1≤x≤3时,y随x的增大而减小,即当x=3时,y=5,则5=−3+2a,解得a=4,所以a=−2或4,故答案为−2或4.

9 《庄子·天下篇》记载“一尺之棰,日取其半,万世不竭”. 如图,直线$l_{1}:y = \frac{1}{2}x + 1与y轴交于点A$,过点$A作x轴的平行线交直线l_{2}:y = x于点O_{1}$,过点$O_{1}作y轴的平行线交直线l_{1}于点A_{1}$,以此类推,令$OA = a_{1}$,$O_{1}A_{1} = a_{2}$,…$$,$O_{n - 1}A_{n - 1} = a_{n}$,若$a_{1} + a_{2} + … + a_{n} \leq S$对任意大于1的整数$n$恒成立,则$S$的最小值为______.

答案： 9.2　[解析]把x=0代入$y=\frac{1}{2}x+1$,得y=1,所以A(0,1)，所以OA=a₁=1;把y=1代入y=x,得x=1,所以O₁(1,1);把x=1代入$y=\frac{1}{2}x+1$,得$y=\frac{1}{2}×1+1=\frac{3}{2}$,所以$A₁(1,\frac{3}{2})$,所以$O₁A₁=a₂=\frac{3}{2}-1=\frac{1}{2}$;把$y=\frac{3}{2}$代入y=x,得$x=\frac{3}{2}$,所以$O₂(\frac{3}{2},\frac{3}{2})$;把$x=\frac{3}{2}$代入$y=\frac{1}{2}x+1$,得$y=\frac{1}{2}×\frac{3}{2}+1=\frac{7}{4}$,所以$A₂(\frac{3}{2},\frac{7}{4})$,所以$O₂A₂=a₃=\frac{7}{4}-\frac{3}{2}=\frac{1}{4}$;…,所以$O_{n-1}A_{n-1}=a_n=(\frac{1}{2})^{n-1}$.因为a₁+a₂+…+aₙ≤S对任意大于1的整数n恒成立,即$S≥a₁+a₂+\cdots+a_n=1+\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{2^{n-1}}=2-\frac{1}{2^{n-1}}$,所以S的最小值为2.故答案为2.