《2025年初中必刷题八年级数学上册北师大版》

1[2025福建莆田质检]利用下列图形,能验证勾股定理的有( )


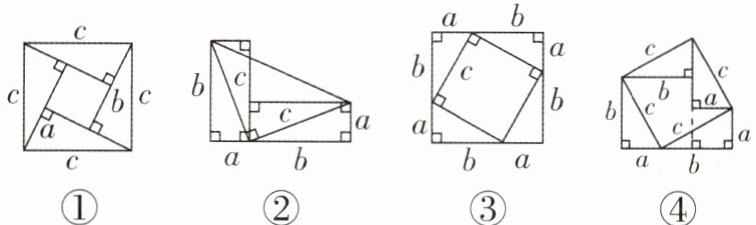
A.1个
B.2个
C.3个
D.4个

答案： D 【解析】①题图中大正方形的面积为$c^{2}$,四个直角三角形的面积和为$4×\frac{1}{2}ab = 2ab$,中间小正方形的边长为$(b - a)$.由大正方形的面积可以表示为四个直角三角形的面积与中间小正方形的面积之和,得$(b - a)^{2}+4×\frac{1}{2}ab=a^{2}+b^{2}=c^{2}$,所以①能验证勾股定理.②如图,四边形ACDE的面积为直角梯形ABDE的面积减去直角三角形ABC的面积,即$\frac{(a + b)(a + b)}{2}-\frac{1}{2}ab=\frac{1}{2}a^{2}+\frac{1}{2}b^{2}+\frac{1}{2}ab$,四边形ACDE的面积还可以表示为等腰直角三角形ACE的面积加上直角三角形CDE的面积,即$\frac{1}{2}c^{2}+\frac{1}{2}ab$,所以$\frac{1}{2}a^{2}+\frac{1}{2}b^{2}+\frac{1}{2}ab=\frac{1}{2}c^{2}+\frac{1}{2}ab$,即$a^{2}+b^{2}=c^{2}$,所以②能验证勾股定理.③题图中大正方形的面积为$(a + b)^{2}=a^{2}+b^{2}+2ab$,大正方形的面积还可以表示为四个直角三角形的面积加上中间小正方形的面积,即$4×\frac{1}{2}ab + c^{2}=2ab + c^{2}$,所以$a^{2}+b^{2}+2ab=2ab + c^{2}$,即$a^{2}+b^{2}=c^{2}$,所以③能验证勾股定理.④题图中五边形的面积为大正方形的面积加上两个直角三角形的面积,即$c^{2}+2×\frac{1}{2}ab=c^{2}+ab$,五边形的面积还可以表示为两个小正方形的面积加上两个直角三角形的面积,即$a^{2}+b^{2}+2×\frac{1}{2}ab=a^{2}+b^{2}+ab$,所以$c^{2}+ab=a^{2}+b^{2}+ab$,即$a^{2}+b^{2}=c^{2}$,所以④能验证勾股定理.故选 D.

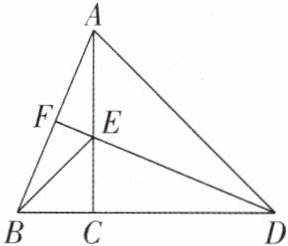
2[2025河南郑州期中]为验证勾股定理,小明进行了如下的思考:如图,在Rt△ABC中,∠ACB=90°,在边AC上截取CE=CB,延长BC到点D,使得CD=CA,连接AD,DE,并延长DE交AB于点F,已知BC=a,AC=b,AB=c.
(1)在验证之前小明发现AB和DE存在着一定的数量关系和位置关系,猜想AB和DE的数量关系和位置关系,并说明理由;
(2)通过以上条件验证勾股定理.

答案： 【解】
(1)$AB = DE$,$AB\perp DE$.理由:因为$\angle ACB=90^{\circ}$,点E在AC上,点D在BC的延长线上,所以$\angle ACB=\angle DCE = 90^{\circ}$.在$\triangle ACB$和$\triangle DCE$中,$\left\{\begin{array}{l}CA = CD,\\\angle ACB=\angle DCE,\\CB = CE,\end{array}\right.$所以$\triangle ACB\cong\triangle DCE$ (SAS),所以$AB = DE$,$\angle BAC=\angle EDC$,所以$\angle AFD=\angle ABC+\angle EDC=\angle ABC+\angle BAC = 90^{\circ}$,所以$AB\perp DE$.
(2)因为$\angle ECB=\angle ACD = 90^{\circ}$,$EC = BC=a$,$DC = AC=b$,所以$S_{\triangle ECB}=\frac{1}{2}a^{2}$,$S_{\triangle ACD}=\frac{1}{2}b^{2}$.因为$DE = AB=c$,$AB\perp DE$,所以$S_{\triangle ADE}=\frac{1}{2}DE\cdot AF$,$S_{\triangle BDE}=\frac{1}{2}DE\cdot BF$,所以$S_{\triangle ADE}+S_{\triangle BDE}=\frac{1}{2}DE\cdot AF+\frac{1}{2}DE\cdot BF=\frac{1}{2}DE(AF + BF)=\frac{1}{2}DE\cdot AB=\frac{1}{2}c^{2}$.因为$S_{\triangle ECB}+S_{\triangle ACD}=S_{\triangle ADE}+S_{\triangle BDE}$,所以$\frac{1}{2}a^{2}+\frac{1}{2}b^{2}=\frac{1}{2}c^{2}$,所以$a^{2}+b^{2}=c^{2}$,所以直角三角形两直角边的平方和等于斜边的平方.

3新考向传统文化在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是有一根竹子原高1丈(1丈=10尺),中间有一处折断,竹梢触地面处离竹根3尺$(1尺=\frac {1}{3}米)$,试问折断处离地面( )

A.4尺
B.3.6尺
C.4.5尺
D.4.55尺

答案： D 【解析】如图,由题意得$\angle ACB = 90^{\circ}$,$BC = 3$尺,$AC+AB = 10$尺.设折断处离地面x尺,则$AB=(10 - x)$尺.在$Rt\triangle ABC$中,由勾股定理得$x^{2}+3^{2}=(10 - x)^{2}$,解得$x = 4.55$,即折断处离地面4.55尺.故选 D.

4[2023山东东营中考]一艘船由A港沿北偏东60°方向航行30km至B港,然后再沿北偏西30°方向航行40km至C港,则A,C两港之间的距离为______km.

答案： 50 【解析】如图,连接AC.由题意得$\angle DAB = 60^{\circ}$,$\angle FBC = 30^{\circ}$,$AD// EF$,所以$\angle DAB=\angle ABE = 60^{\circ}$,所以$\angle ABC=180^{\circ}-\angle ABE-\angle FBC = 90^{\circ}$.在$Rt\triangle ABC$中,$AB = 30km$,$BC = 40km$,$AC^{2}=AB^{2}+BC^{2}=30^{2}+40^{2}=2500$,所以$AC = 50km$,所以A,C两港之间的距离为50 km,故答案为50.

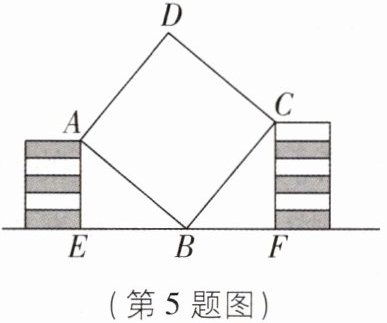
5小亮用11块高度都是2cm的相同长方体小木块垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形木板ABCD,截面如图所示.两木墙的高度分别为AE与CF的长,点B在EF上,则正方形木板ABCD的面积为______$cm^{2}$.

答案： 244 【解析】在正方形木板ABCD中,$\angle ABC = 90^{\circ}$,$AB = BC$.因为$AE\perp EF$,$CF\perp EF$,所以$\angle AEB=\angle BFC = 90^{\circ}$,所以$\angle EAB+\angle ABE = 90^{\circ}$.因为$\angle ABC = 90^{\circ}$,所以$\angle ABE+\angle CBF = 90^{\circ}$,所以$\angle EAB=\angle CBF$.在$\triangle ABE$和$\triangle BCF$中,$\left\{\begin{array}{l}\angle EAB=\angle CBF,\\\angle AEB=\angle BFC = 90^{\circ},\\AB = BC,\end{array}\right.$所以$\triangle ABE\cong\triangle BCF$ (AAS),所以$AE = BF=2×5 = 10(cm)$.因为$CF = 2×6 = 12(cm)$,所以在$Rt\triangle BCF$中,$BC^{2}=BF^{2}+CF^{2}=10^{2}+12^{2}=244$,所以$S_{正方形ABCD}=BC^{2}=244cm^{2}$,即正方形木板ABCD的面积为$244cm^{2}$.

6[2025江苏徐州期中]如图,在笔直的公路AB旁有一个城市书房C,C到公路AB的距离CD为80米,AC为100米,BC为300米.一辆公交车以10米/秒的速度从A处出发,沿公路AB向B处行驶.若公交车鸣笛声会使以公交车为中心170米范围内受到噪音影响,则公交车在公路AB上行驶时,至少______秒不鸣笛才能使在城市书房C中看书的读者不受噪音影响.

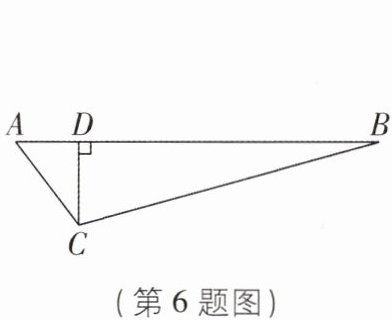
答案： 21 【解析】如图,在BD上取一点E,连接CE,使$CE = 170$米.因为$\angle CDE = 90^{\circ}$,$CD = 80$米,所以$DE^{2}=CE^{2}-CD^{2}=170^{2}-80^{2}=22500$,所以$DE = 150$米.因为$CD = 80$米,$AC = 100$米$＜170$米,所以公交车在EA段不能鸣笛,$AD^{2}=AC^{2}-CD^{2}=100^{2}-80^{2}=3600$,所以$AD = 60$米,所以$EA=AD + DE=60 + 150=210$米.因为$\frac{210}{10}=21$秒,所以公交车在公路AB上行驶时,至少21秒不鸣笛才能使在城市书房C中看书的读者不受噪音影响.故答案为21.

7一辆装满货物的卡车,高2.5m,宽1.6m,要开进上边是半圆,下边是长方形的隧道,如图所示,已知半圆的直径为2m,长方形的另一条边长是2.3m.
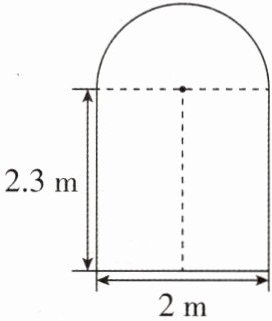
(1)此卡车是否能通过隧道?试说明你的理由.
(2)为了适应车流量的增加,现把隧道改为双行道,要使宽为1.2m,高为2.8m的卡车能安全通过,那么此隧道的宽至少增加到多少?

答案： 思路分析 过隧道问题
【解】
(1)该卡车能通过隧道.理由如下:如图
(1),MN为卡车的宽度,分别过M,N作AB的垂线交半圆于C,D,连接CD,过AB的中点O作$OE\perp CD$,E为垂足,连接OC.易知$CD = MN=1.6m$,$AB = 2m$,所以由对称可得$CE = DE = 0.8m$,$OC = OA=1m$.在$Rt\triangle OCE$中,$OE^{2}=OC^{2}-CE^{2}=0.36$,即$OE = 0.6m$,所以$CM=2.3 + 0.6=2.9(m)＞2.5m$,所以这辆卡车能通过隧道.
(2)如图
(2),EC为卡车的宽度,过E作AH 的垂线交半圆于B,垂足为F,连接OB,过B 作BG⊥CO,交CO的延长线于G.根据题意可知CG=BE=2.8m,BG=0F=EC=1.2m,EF=AD=2.3m,所以BF=2.8−2.3=0.5(m).根据勾股定理得OA²=0B²=BF²+OF²=0.5²+1.2²=1.69,即0A=1.3m,所以隧道的宽至少增加到1.3×2=2.6(m).