《2025年初中必刷题八年级数学上册北师大版》

1 一次函数的图象如图所示,那么这个一次函数的表达式是( )

A.$ y = - 2 x - 2 $
B.$ y = 2 x - 2 $
C.$ y = - 2 x + 2 $
D.$ y = 2 x + 2 $

答案： A 【解析】设这个一次函数的表达式为 y=kx+b. 将(-1,0)与(0,-2)代入，得{-k+b=0,b=-2,解得{k=-2,b=-2,则这个一次函数的表达式为 y=-2x-2. 故选 A.

2 已知$ y 是 x $的一次函数,下表给出了部分对应值,则$ m $的值是____.
| $ x $ | 2 | 4 | 5 |
| $ y $ | -1 | -5 | $ m $ |

答案： -7 【解析】设 y=kx+b. 把 x=2,y=-1 和 x=4,y=-5 代入 y=kx+b，得{2k+b=-1,4k+b=-5,解得{k=-2,b=3,所以 y=-2x+3. 把 x=5 代入 y=-2x+3,得 y=-2×5+3=-7,所以 m=-7. 故答案为-7.

3 已知某一次函数的图象与正比例函数$ y = 2 x $的图象平行,且与$ y 轴的交点和直线 y = 3 x + 4 与 y $轴的交点为同一点,则此一次函数的表达式为____.

答案： y=2x+4 【解析】设该一次函数的表达式为 y=kx+b. 因为一次函数 y=kx+b 的图象与正比例函数 y=2x 的图象平行,所以 k=2. 在 y=3x+4 中,当 x=0 时,y=4,所以图象与 y 轴交于点(0,4). 将点(0,4)代入一次函数 y=2x+b 中,得 b=4,所以此一次函数的表达式为 y=2x+4. 故答案为 y=2x+4.

4 如图,直线$ l _ { 1 } 的表达式为 y = 3 x - 2 $,且直线$ l _ { 1 } 与 x 轴交于点 D $. 直线$ l _ { 2 } 与 x 轴交于点 A $,且经过点$ B $,直线$ l _ { 1 } 与 l _ { 2 } 交于点 C ( m , 3 ) $.
(1)求点$ D 和点 C $的坐标；
(2)求直线$ l _ { 2 } $的表达式；
(3)利用函数图象写出关于$ x $,$ y 的二元一次方程组 \left\{ \begin{array} { l } { y = 3 x - 2 , } \\ { 6 x + 7 y = 31 } \end{array} \right. $的解.

答案：
(1)在 y=3x-2 中,令 y=0,即 3x-2=0,解得 x=$\frac{2}{3}$,所以 D($\frac{2}{3}$,0).因为点 C(m,3)在直线 y=3x-2 上,所以 3m-2=3,解得 m=$\frac{5}{3}$,所以 C($\frac{5}{3}$,3).
(2)设直线 l₂的表达式为 y=kx+b(k≠0).由图象可知 B(4,1).由题意得{$\frac{5}{3}$k+b=3,4k+b=1,解得{k=-$\frac{6}{7}$,b=$\frac{31}{7}$,所以直线 l₂的表达式为 y=-$\frac{6}{7}$x+$\frac{31}{7}$.
(3)将 y=-$\frac{6}{7}$x+$\frac{31}{7}$ 变形为 6x+7y=31.由图象可知,关于 x,y 的二元一次方程组{y=3x-2,6x+7y=31 的解为{x=$\frac{5}{3}$,y=3.

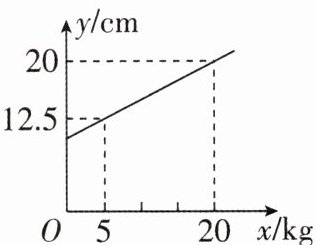
5 在弹性限度内,弹簧的长度$ y ( \mathrm { cm } ) 与所挂物体的质量 x ( \mathrm { kg } ) $之间是一次函数关系,图象如图所示,则弹簧不挂物体时的长度是( )

A.$ 9 \mathrm { cm } $
B.$ 10 \mathrm { cm } $
C.$ 10.5 \mathrm { cm } $
D.$ 11 \mathrm { cm } $

答案： B 【解析】设 y 与 x 间的关系式为 y=kx+b. 将(5,12.5),(20,20)代入,得{12.5=5k+b,20=20k+b,解得{k=$\frac{1}{2}$,b=10,所以 y=$\frac{1}{2}$x+10. 当 x=0 时,y=10,即弹簧不挂物体时的长度是 10 cm. 故选 B.

6 [2025湖北武汉质检]如图表示的是甲、乙两船沿相同路线从A港出发到B港的行驶过程中,路程$ y ( \mathrm { km } ) 随时间 t ( \mathrm { h } ) $变化的图象,则乙船出发多长时间赶上甲船( )

A.$ 1.5 \mathrm { h } $
B.$ 2 \mathrm { h } $
C.$ 2.5 \mathrm { h } $
D.$ 3.5 \mathrm { h } $

答案： B 【解析】设 y甲=kx,将(8,160)代入得 160=8k,解得 k=20,所以 y甲=20x(0≤x≤8). 设 y乙=ax+b,将(2,0),(6,160)代入得{0=2a+b,160=6a+b,解得{a=40,b=-80,所以 y乙=40x-80(2≤x≤6). 联立得{y=20x,y=40x-80,解得{x=4,y=80,所以乙船出发 4-2=2(h)赶上甲船. 故选 B.

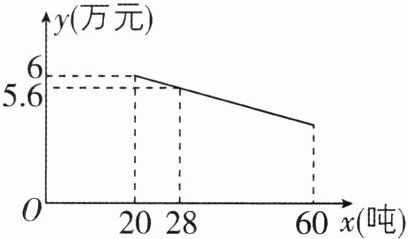
7 [2024江西九江期末]某工厂生产一种产品,当生产数量至少为20吨,但不超过60吨时,每吨的成本$ y $(万元)与生产数量$ x $(吨)之间是一次函数关系,其图象如图所示.
(1)求出$ y 关于 x $的函数表达式；
(2)如果每吨的成本是4.8万元,求该产品的生产数量.

答案：
(1)设 y 关于 x 的函数表达式是 y=kx+b. 因为点(20,6),(28,5.6)在该函数图象上,所以{20k+b=6,28k+b=5.6,解得{k=-0.05,b=7,即 y 关于 x 的函数表达式是 y=-0.05x+7.
(2)当 y=4.8 时,4.8=-0.05x+7,解得 x=44.答:如果每吨的成本是 4.8 万元,那么该产品的生产数量是 44 吨.