第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1 [中]在平面直角坐标系中,已知点 A 与点 B 关于 x 轴对称,点 B 与点 C 关于 y 轴对称,点 A 的坐标为(-1,2),则点 C 的坐标为 ( )
A.(-1,2)
B.(1,-2)
C.(-1,-2)
D.(2,-1)
A.(-1,2)
B.(1,-2)
C.(-1,-2)
D.(2,-1)
答案:
B [解析]
$\begin{cases}A(-1,2)\xlongequal{关于x轴对称}B(-1,-2)\xlongequal{关于y轴对称}C(1,-2)\end{cases}$
故选B.
$\begin{cases}A(-1,2)\xlongequal{关于x轴对称}B(-1,-2)\xlongequal{关于y轴对称}C(1,-2)\end{cases}$
故选B.
2 [较难]如图,在平面直角坐标系中,对△ABC 进行循环往复的轴对称变换,若原来点 A 坐标是(1,2),则经过第 2021 次变换后点 A 的对应点的坐标为 ( )

A.(1,-2)
B.(-1,-2)
C.(-1,2)
D.(1,2)

A.(1,-2)
B.(-1,-2)
C.(-1,2)
D.(1,2)
答案:
C [解析]点A第1次关于y轴对称后在第二象限,点A第2次关于x轴对称后在第三象限,点A第3次关于y轴对称后在第四象限,点A第4次关于x轴对称后在第一象限,即点A回到原始位置,所以每4次对称为一个循环组,依次循环.因为2021÷4 = 505……1,所以点A经过第2021次变换后的位置与第1次变换后的位置相同,在第二象限,坐标为(−1,2).故选C.
3 [2024 吉林松原质检,中]如图,在平面直角坐标系中摆放着一个轴对称图形,其中点 A(-6,6)的对称点 A'坐标为(0,6),点 M(m,n)为图形上的一点,则点 M 在图形上的对称点坐标为____.


答案:
(−6−m,n) [解析]因为点A(−6,6)的对称点A'坐标为(0,6),所以该图形对称轴为直线x = −3.设点M在图形上的对称点坐标为(m',n'),所以$\frac{m + m'}{2}=-3$,n' = n,所以m' = −6−m,所以点M在图形上的对称点坐标为(−6−m,n).故答案为(−6−m,n).
4 [2024 河南许昌质检,中]如图,已知平面直角坐标系中的两点 A(0,4),B(1,0),P 为线段 AB 上一动点(不与点 A,B 重合),作点 B 关于射线 OP 的对称点 C,则线段 AC 长度的取值范围是____.
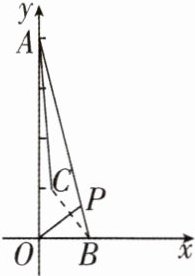

答案:
3≤AC<$\sqrt{17}$ [解析]如图,连接OC.因为A(0,4),B(1,0),所以OA = 4,OB = 1,所以$AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{17}$.因为C是点B关于射线OP的对称点,所以OC = OB = 1.因为OA - OC≤AC,所以AC≥3.因为P为线段AB上一动点(不与点A,B重合),所以线段AC长度的取值范围是3≤AC<$\sqrt{17}$.故答案为3≤AC<$\sqrt{17}$.

3≤AC<$\sqrt{17}$ [解析]如图,连接OC.因为A(0,4),B(1,0),所以OA = 4,OB = 1,所以$AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{17}$.因为C是点B关于射线OP的对称点,所以OC = OB = 1.因为OA - OC≤AC,所以AC≥3.因为P为线段AB上一动点(不与点A,B重合),所以线段AC长度的取值范围是3≤AC<$\sqrt{17}$.故答案为3≤AC<$\sqrt{17}$.

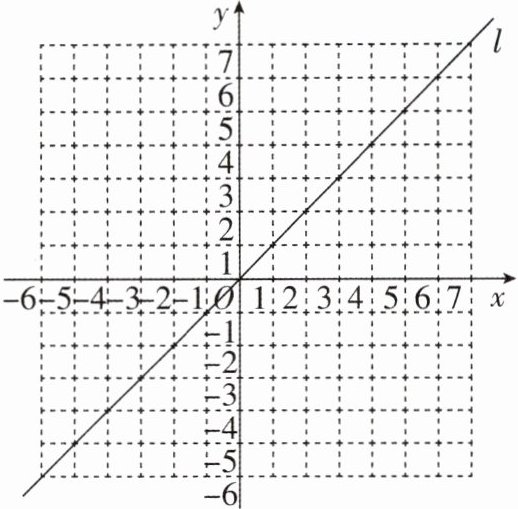
5 [2025 黑龙江哈尔滨质检,中]如图,在平面直角坐标系中,直线 l 为第一、三象限的角平分线.点 P 关于 y 轴的对称点为 P 的一次反射点,记为$ P_1,$点$ P_1 $关于直线 l 的对称点称为点 P 的二次反射点,记为$ P_2. $例如,点(-1,2)的一次反射点为(2,1),二次反射点为(2,1).根据定义,回答下列问题:
(1)点(3,-4)的一次反射点为____,二次反射点为____;
(2)若 P(m + 1,2n - 1)的一次反射点和 Q(-3,4)的二次反射点重合,求 m + n 的值.
(1)点(3,-4)的一次反射点为____,二次反射点为____;
(2)若 P(m + 1,2n - 1)的一次反射点和 Q(-3,4)的二次反射点重合,求 m + n 的值.

答案:
[解]
(1)根据题意,可得点(3,−4)的一次反射点为(−3,−4),二次反射点为(−4,−3).故答案为(−3,−4),(−4,−3).
(2)因为P(m + 1,2n - 1),所以P的一次反射点为(−m - 1,2n - 1).因为Q(−3,4),所以Q的一次反射点为(3,4),Q的二次反射点为(4,3).因为P(m + 1,2n - 1)的一次反射点和Q(−3,4)的二次反射点重合,所以−m - 1 = 4,2n - 1 = 3,所以m = −5,n = 2,所以m + n = −5 + 2 = −3.
(1)根据题意,可得点(3,−4)的一次反射点为(−3,−4),二次反射点为(−4,−3).故答案为(−3,−4),(−4,−3).
(2)因为P(m + 1,2n - 1),所以P的一次反射点为(−m - 1,2n - 1).因为Q(−3,4),所以Q的一次反射点为(3,4),Q的二次反射点为(4,3).因为P(m + 1,2n - 1)的一次反射点和Q(−3,4)的二次反射点重合,所以−m - 1 = 4,2n - 1 = 3,所以m = −5,n = 2,所以m + n = −5 + 2 = −3.
6 [2024 广东佛山顺德区期中,中]如图,在平面直角坐标系中,点 A,B 的坐标分别为(2,8)和(6,0),C 是 y 轴上的一个动点,且 A,B,C 三点不在同一条直线上.
(1)求 AB 的长;
(2)求△ABC 的周长的最小值.
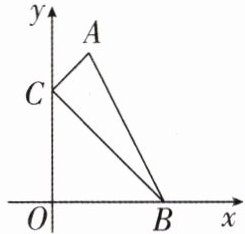
(1)求 AB 的长;
(2)求△ABC 的周长的最小值.

答案:
[解]
(1)过点A作AD⊥OB于D,如图,则∠ADB = 90°.因为点A,B的坐标分别为(2,8)和(6,0),所以OD = 2,AD = 8,OB = 6,所以BD = 4,所以$AB=\sqrt{AD^{2}+DB^{2}}=\sqrt{8^{2}+4^{2}} = 4\sqrt{5}$.
(2)因为AB长度一定,所以要使△ABC的周长最小,需AC + BC的值最小.作A关于y轴的对称点A',连接BA'交y轴于点C',过点A'作A'E⊥x轴于点E,连接A'C,如图.因为AC + BC = A'C + BC≥A'B,所以当A',C,B三点共线,即C与C'重合时,△ABC的周长最小,最小值为A'B + AB的值.由轴对称的性质得A'(−2,8),所以E(−2,0).在Rt△A'EB中,A'E = 8,EB = 8,所以$A'B=\sqrt{8^{2}+8^{2}} = 8\sqrt{2}$,所以△ABC的周长的最小值为A'B + AB = 8$\sqrt{2}+4\sqrt{5}$.

[解]
(1)过点A作AD⊥OB于D,如图,则∠ADB = 90°.因为点A,B的坐标分别为(2,8)和(6,0),所以OD = 2,AD = 8,OB = 6,所以BD = 4,所以$AB=\sqrt{AD^{2}+DB^{2}}=\sqrt{8^{2}+4^{2}} = 4\sqrt{5}$.
(2)因为AB长度一定,所以要使△ABC的周长最小,需AC + BC的值最小.作A关于y轴的对称点A',连接BA'交y轴于点C',过点A'作A'E⊥x轴于点E,连接A'C,如图.因为AC + BC = A'C + BC≥A'B,所以当A',C,B三点共线,即C与C'重合时,△ABC的周长最小,最小值为A'B + AB的值.由轴对称的性质得A'(−2,8),所以E(−2,0).在Rt△A'EB中,A'E = 8,EB = 8,所以$A'B=\sqrt{8^{2}+8^{2}} = 8\sqrt{2}$,所以△ABC的周长的最小值为A'B + AB = 8$\sqrt{2}+4\sqrt{5}$.

7 核心素养 几何直观 [难]已知三点 A(1,2),B(1,3),C(0,6),点 P 为 y 轴上一动点.
(1)在图中找到点 P,使得△OAP 与△CBP 周长的和取得最小值,此时点 P 的坐标应为____;
(2)当∠APB = 40°时,∠OAP + ∠PBC 的度数为____.

(1)在图中找到点 P,使得△OAP 与△CBP 周长的和取得最小值,此时点 P 的坐标应为____;
(2)当∠APB = 40°时,∠OAP + ∠PBC 的度数为____.

答案:
(1)$(0,\frac{5}{2})$ [解析]
(1)如图
(1),因为A(1,2),B(1,3),C(0,6),所以OA,BC是定长,所以当点P在线段OC上时,△OAP与△CBP周长的和取得最小值.因为OP + PC = OC = 6,所以△OAP与△CBP周长的和为OA + AP + OP + PC + BC + BP = OA + BC + OC + AP + BP,所以当AP + BP的值最小时,△OAP与△CBP周长的和取得最小值.作点A关于y轴的对称点A',连接A'B,则A'B与y轴的交点即为所求的点P.易得A'(−1,2),P是A'B的中点,所以$P(\frac{-1 + 1}{2},\frac{2 + 3}{2})$,即$P(0,\frac{5}{2})$.故答案为$(0,\frac{5}{2})$.
(2)175° [解析]
(2)如图
(2),过点B作BD⊥OC于D,作点A关于y轴的对称点A',AA'交y轴于点E,连接A'B,OA',OB,AB.因为CD = OD = 3,所以BC = OB,所以∠BCO = ∠BOC.由轴对称的性质得OA = OA',∠OAE = ∠OA'E,∠AOE = ∠A'OE.因为AB = AE = 1,AA' = OE = 2,∠BAA' = ∠AEO = 90°,所以△A'AB≌△OEA(SAS),所以∠BA'A = ∠AOE,A'B = OA = OA'.因为∠AOE + ∠OAE = 90°,所以∠OA'E + ∠AA'B = 90°,即∠BA'O = 90°.因为A'B = OA = OA',所以△OA'B是等腰直角三角形,∠BOA' = 45°,所以∠BOD + ∠A'OE = ∠BCD + ∠AOE = 45°.因为∠APB = 40°,所以∠ABP + ∠BAP = 140°,所以∠OAP + ∠PBC = 360° - 140° - 45° = 175°.故答案为175°.


(1)$(0,\frac{5}{2})$ [解析]
(1)如图
(1),因为A(1,2),B(1,3),C(0,6),所以OA,BC是定长,所以当点P在线段OC上时,△OAP与△CBP周长的和取得最小值.因为OP + PC = OC = 6,所以△OAP与△CBP周长的和为OA + AP + OP + PC + BC + BP = OA + BC + OC + AP + BP,所以当AP + BP的值最小时,△OAP与△CBP周长的和取得最小值.作点A关于y轴的对称点A',连接A'B,则A'B与y轴的交点即为所求的点P.易得A'(−1,2),P是A'B的中点,所以$P(\frac{-1 + 1}{2},\frac{2 + 3}{2})$,即$P(0,\frac{5}{2})$.故答案为$(0,\frac{5}{2})$.
(2)175° [解析]
(2)如图
(2),过点B作BD⊥OC于D,作点A关于y轴的对称点A',AA'交y轴于点E,连接A'B,OA',OB,AB.因为CD = OD = 3,所以BC = OB,所以∠BCO = ∠BOC.由轴对称的性质得OA = OA',∠OAE = ∠OA'E,∠AOE = ∠A'OE.因为AB = AE = 1,AA' = OE = 2,∠BAA' = ∠AEO = 90°,所以△A'AB≌△OEA(SAS),所以∠BA'A = ∠AOE,A'B = OA = OA'.因为∠AOE + ∠OAE = 90°,所以∠OA'E + ∠AA'B = 90°,即∠BA'O = 90°.因为A'B = OA = OA',所以△OA'B是等腰直角三角形,∠BOA' = 45°,所以∠BOD + ∠A'OE = ∠BCD + ∠AOE = 45°.因为∠APB = 40°,所以∠ABP + ∠BAP = 140°,所以∠OAP + ∠PBC = 360° - 140° - 45° = 175°.故答案为175°.


查看更多完整答案,请扫码查看


