《2025年初中必刷题八年级数学上册北师大版》

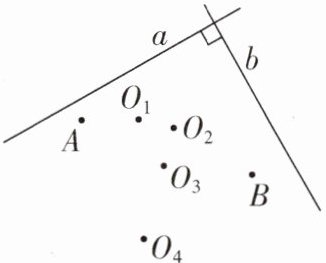
1[中]如图,直线a⊥b,以平行于a的直线为x轴,以平行于b的直线为y轴,建立平面直角坐标系,若A(-3,2),B(2,-3),则坐标系的原点最有可能是( )
$A.O_1$
$B.O_2$
$C.O_3$
$D.O_4$

答案：
B 【解析】如图,因为A(-3,2),B(2,-3),直线a⊥b,以平行于a的直线为x轴,以平行于b的直线为y轴,所以建立如图所示的平面直角坐标系,则坐标系的原点最有可能是O₂.故选B.

2[中]已知等腰△ABC,建立适当的平面直角坐标系后,其三个顶点的坐标分别为A(m,0),B(m+4,2),C(m+4,-3),则下列关于该三角形的三边关系正确的是( )

A.AC= BC≠AB
B.AB= AC≠BC
C.AB= BC≠AC
D.AB= AC= BC

答案：
A 【解析】建立平面直角坐标系如图所示,令BC交x轴于点D.因为AD=4,BD=2,CD=3,所以BC=5,AB=√(AD²+BD²)=√(4²+2²)=2√5,AC=√(AD²+CD²)=√(4²+3²)=5,所以AC=BC≠AB.故选A.

3[中]数学中有许多形状优美、寓意美好的曲线,建立如图所示的直角坐标系,曲线C就是其中之一。给出下列三个结论：①曲线C恰好经过6个整点(即横、纵坐标均为整数的点)；②曲线C在第一、二象限中的任意一点到原点的距离大于1；③曲线C所围成的“心形”区域的面积小于3。其中正确结论的序号是( )

A.①
B.②
C.①②
D.①②③

答案： C 【解析】①观察题图可得曲线C经过的整点有6个,故正确;②曲线C在第一、二象限中的任意一点到原点的距离大于1,坐标轴上的点不属于任何一个象限,故正确;③由题图可知,曲线C经过的点有(1,1),(-1,1),(0,1),(-1,0),(1,0),(0,-1),故在横轴以上的部分面积大于2,而横轴以下的部分面积大于1,所以曲线C所围成的"心形"区域的面积大于3,故原结论错误.故选C.

4[中]在平面直角坐标系中,点A的坐标为(3,0),点B的坐标为(-1,0),点C在y轴上。如果△ABC的面积等于6,那么点C的坐标为______。

答案： (0,3)或(0,-3) 【解析】因为点A的坐标为(3,0),点B的坐标为(-1,0),所以点A,B都在x轴上,且AB=3-(-1)=4.因为，点C在y轴上,所以设点C的坐标为(0,y).因为△ABC的面积等于6,所以(1/2)×4×|y|=6,解得y=±3,所以点C的坐标为(0,3)或(0,-3).

5[新考法][2025安徽黄山期中,中]有甲、乙、丙三人,他们所在的位置不同,他们三人都以相同的单位长度建立不同的平面直角坐标系。甲说：“如果以我为坐标原点,那么乙的位置是(4,3)。”丙说：“如果以我为坐标原点,那么乙的位置是(-3,-4)。”根据以上内容,回答问题：如果以丙为坐标原点,那么甲的位置是______。

答案： (-7,-7) 【解析】以甲为坐标原点,乙的位置是(4,3),则以乙为坐标原点,甲的位置是(-4,-3);以丙为坐标原点,乙的位置是(-3,-4),则以乙为坐标原点,丙的位置是(3,4),所以以丙为坐标原点,甲的位置是(-7,-7).故答案为(-7,-7).

6[中]如图(1)所示,已知四边形ABCD,∠A= 90°,AB= 3m,BC= 12m,CD= 13m,DA= 4m。
(1)试说明：BD⊥CB；
(2)求四边形ABCD的面积；
(3)如图(2),以A为坐标原点,分别以AB,AD所在直线为x轴、y轴建立直角坐标系,点P在y轴上,若$S_{△PBD}= \frac{1}{4}S_{四边形ABCD}$,求点P的坐标。

答案： 【解】
(1)因为AD=4m,AB=3m,∠BAD=90°,所以BD=√(AD²+AB²)=5m.因为BC=12m,CD=13m,所以BD²+BC²=5²+12²=13²=CD²,所以BD⊥CB.
(2)S四边形ABCD=S△ABD+S△BCD=(1/2)×3×4+(1/2)×12×5=6+30=36(m²).
(3)因为S△PBD=(1/4)S四边形ABCD,所以(1/2)·PD·AB=(1/4)×36,即(1/2)·PD×3=9,解得PD=6.因为D(0,4),点P在y轴上,所以P的坐标为(0,-2)或(0,10).

7[核心素养推理能力][较难]定义：在平面直角坐标系xOy中,已知点$P_1(a,b),P_2(c,b),P_3(c,d),$这三个点中任意两点间的距离的最小值称为点$P_1,P_2,P_3$的“最佳间距”。例如：如图,点$P_1(-1,2),P_2(1,2),P_3(1,3)$的“最佳间距”是1。
(1)理解：点$Q_1(2,1),Q_2(4,1),Q_3(4,4)$的“最佳间距”是______。
(2)探究：已知点O(0,0),A(-3,0),B(-3,y)。
①若点O,A,B的“最佳间距”是1,求y的值；
②点O,A,B的“最佳间距”的最大值为______。

答案： 【解】
(1)因为点Q₁(2,1),Q₂(4,1),Q₃(4,4),所以Q₁Q₂=2,Q₂Q₃=3,Q₁Q₂//x轴,Q₂Q₃⊥x轴,所以Q₁Q₂⊥Q₂Q₃.因为垂线段最短,所以Q₁Q₃＞2,所以点Q₁(2,1),Q₂(4,1),Q₃(4,4)的"最佳间距"是2.故答案为2.
(2)①因为点O(0,0),A(-3,0),B(-3,y),所以AB⊥OA,OA=3,所以OB＞OA.因为点O,A,B的"最佳间距"是1,所以AB=1,所以y=±1.
②当-3≤y≤3时,点O,A,B的"最佳间距"是|y|=AB≤3;当y＞3或y＜-3时,AB＞3,点O,A,B的"最佳间距"是OA=3,所以点O,A,B的"最佳间距"的最大值为3.故答案为3.