《2025年初中必刷题八年级数学上册北师大版》

1[2025湖北孝感安陆期中,中]若一个自然数的算术平方根是n,则从小到大排序的下一个自然数的算术平方根是( )

A.$\sqrt{n^2 + 1}$
B.$\sqrt{n} + 1$
C.$n + 1$
D.$\sqrt{n + 1}$

答案： A　[解析]一个自然数的算术平方根是$n$，则这个自然数是$n^2$，则从小到大排序的下一个自然数为$n^2 + 1$，其算术平方根为$\sqrt{n^2 + 1}$，故选A.

2[2025山东济南调研,中]若$\sqrt{a} = 3$,$|b| = 5$,且$ab ＜ 0$,则$a + b$的算术平方根为( )

A.4
B.2
C.±2
D.3

答案：
B　[解析] $\sqrt{a}=3$，$ab\lt0$，$a\gt0$，$a$，$b$异号，$a\gt0$，$b\lt0$，$\sqrt{a}=3$，$\vert b\vert = 5$，$a = 9$，$b = -5$，$\sqrt{a + b}=\sqrt{9 - 5}=2$

3[2025河北保定校级期中,中]将长和宽分别为2和1的长方形按如图所示剪开,拼成一个与长方形面积相等的正方形,则该正方形的边长为____.

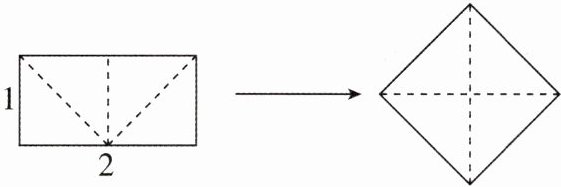
答案： $\sqrt{2}$　[解析]设正方形的边长为$x$.由题意得$x^2 = 2×1$，所以$x = \sqrt{2}$，所以该正方形的边长为$\sqrt{2}$.故答案为$\sqrt{2}$.

4[2025山西大同期末,中]请你观察思考下列计算过程:
因为$11^2 = 121$,所以$\sqrt{121} = 11$.
同理,因为$111^2 = 12321$,所以$\sqrt{12321} = 111$.
因为1$111^2 = 1234321$,所以$\sqrt{1234321} = $____.
由此猜想:$\sqrt{1234567654321} = $____.

答案： 1111 1111111　[解析]因为$11^2 = 121$，所以$\sqrt{121}=11$.同理，因为$111^2 = 12321$ ,所以$\sqrt{12321}=111$.因为$1111^2 = 1234321$，所以$\sqrt{1234321}=1111$.由此猜想$\sqrt{1234567654321}=1111111$.故答案为1111，1111111.

5[2025江苏盐城质检,较难]若$|a - 2022| + \sqrt{b + 2022} = 2$,其中a,b均为整数,则$|a + b| = $____.

答案： 4或2或0　[解析]因为$\vert a - 2022\vert+\sqrt{b + 2022}=2$，其中$a$，$b$均为整数，且$\vert a - 2022\vert\geq0$，$\sqrt{b + 2022}\geq0$，所以可分以下三种情况：①$\vert a - 2022\vert = 0$，$\sqrt{b + 2022}=2$，解得$a = 2022$，$b = -2018$，则$\vert a + b\vert = 4$；②$\vert a - 2022\vert = 1$，$\sqrt{b + 2022}=1$，解得$a = 2021$或2023，$b = -2021$，则$\vert a + b\vert = 0$或2；③$\vert a - 2022\vert = 2$，$\sqrt{b + 2022}=0$，解得$a = 2024$或2020，$b = -2022$，则$\vert a + b\vert = 2$.综上所述，$\vert a + b\vert = 4$或2或0.故答案为4或2或0.

6[2025福建厦门校级期中,较难]对于一个各数位上的数字均不为0的三位自然数x,若x的百位数字与十位数字的平均数等于个位数字,则称x为“均衡数”.将“均衡数”x的百位数字与十位数字交换位置后得到的新数再与x相加的和记为$F(x)$.若三位数n是“均衡数”,满足百位数字小于十位数字,$\sqrt{\frac{F(n)}{111}}$为整数,且$F(n)$能被n的十位数字与百位数字的差整除,则n的值为____.

答案： 132或798　[解析]设$n = 100a + 10b + c$（$1\leq a\lt b\leq9$，$1\lt c\lt9$，$a$，$b$，$c$均为整数），则$a + b = 2c$，所以$F(n)=100a + 10b + c + 100b + 10a + c = 222c$，所以$\sqrt{\frac{F(n)}{111}}=\sqrt{\frac{222c}{111}}=\sqrt{2c}$.因为$\sqrt{\frac{F(n)}{111}}$是一个整数，$1\lt c\lt9$，所以$2c = 4$或$2c = 16$，则$c = 2$或8，所以$F(n)=444$或1776.①当$F(n)=444$时，因为$F(n)$能被$n$的十位数字与百位数字的差整除，所以$\frac{444}{b - a}$为整数，所以$b - a = 1$或2或3或4或6.因为$a + b = 2c = 4$，所以易知$b = 3$，$a = 1$.②当$F(n)=1776$时，因为$\frac{1776}{b - a}$为整数，所以$b - a = 1$或2或3或4或6或8.因为$a + b = 2c = 16$，所以易知$b = 9$，$a =7$，所以$n = 132$或798.故答案为132或798.

7[2025浙江金华期中,中]对于含算术平方根的算式,在有些情况下,可以不需要计算出结果也能将算术平方根符号去掉,例如:$\sqrt{(1 - \frac{1}{2})^2} = \sqrt{(\frac{1}{2})^2} = \frac{1}{2} = 1 - \frac{1}{2}$,$\sqrt{(\frac{1}{2} - 1)^2} = \sqrt{(-\frac{1}{2})^2} = \frac{1}{2} = 1 - \frac{1}{2}$.
观察上述式子的特征,解答下列问题:
(1)把下列各式写成去掉算术平方根符号的形式(不用写出计算结果):
$\sqrt{(10 - 6)^2} = $____;$\sqrt{(7 - 9)^2} = $____;
(2)当$a ＞ b$时,$\sqrt{(a - b)^2} = $____;当$a ＜ b$时,$\sqrt{(a - b)^2} = $____;
(3)计算:$\sqrt{(\frac{1}{3} - \frac{1}{2})^2} + \sqrt{(\frac{1}{4} - \frac{1}{3})^2} + \sqrt{(\frac{1}{5} - \frac{1}{4})^2} + … + \sqrt{(\frac{1}{2023} - \frac{1}{2022})^2}$.

答案：
(1)10 - 6，9 - 7；
(2)$a - b$，$b - a$；
(3)$\frac{2021}{4046}$　[解]
(1)由题意可知$\sqrt{(10 - 6)^2}=10 - 6$，$\sqrt{(7 - 9)^2}=9 - 7$.故答案为10 - 6，9 - 7.
(2)由题意可知当$a＞b$时，$\sqrt{(a - b)^2}=a - b$；当$a＜b$时，$\sqrt{(a - b)^2}=b - a$.故答案为$a - b$，$b - a$.
(3)原式$=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\cdots+\frac{1}{2022}-\frac{1}{2023}=\frac{1}{2}-\frac{1}{2023}=\frac{2021}{4046}$.

8核心素养推理能力[2025山西太原调研,较难]观察表格并回答下列问题.
| $a(a ＞ 0)$ | …$$ | 0.0001 | 0.01 | 1 | 100 | 10000 | …$$ |
| $\sqrt{a}$ | …$$ | 0.01 | $x$ | 1 | $y$ | 100 | …$$ |
(1)表格中$x = $____,$y = $____.
(2)①已知$\sqrt{6} \approx 2.45$,则$\sqrt{0.06} \approx$____;
②已知$\sqrt{0.0012} \approx 0.03464$,$\sqrt{2m} \approx 34.64$,求m的值.

答案： 【解析】：
(1) 对于表格中的$x$和$y$，需要根据平方根的定义和性质来求解，平方根是若一个数的平方等于另一个数，则这个数就是另一个数的平方根，而且正数的平方根有两个，它们互为相反数，由于表格中给出的是算术平方根，是非负数，所以只取正值。
对于$x$，当$a=0.01$时，其平方根应为$\sqrt{0.01}$，根据平方根的性质，我们知道$0.1 × 0.1 = 0.01$，所以$x=0.1$。
对于$y$，当$a=100$时，其平方根应为$\sqrt{100}$，根据平方根的性质，我们知道$10 × 10 = 100$，所以$y=10$。
(2) ① 对于$\sqrt{0.06}$的近似值，可以根据已知的$\sqrt{6} \approx 2.45$来推导，由于$0.06 = 6 ÷ 100$，根据平方根的性质，$\sqrt{0.06} = \sqrt{6 ÷ 100} = \frac{\sqrt{6}}{10} \approx \frac{2.45}{10} = 0.245$。
② 对于$m$的值，可以根据已知的$\sqrt{0.0012} \approx 0.03464$和$\sqrt{2m} \approx 34.64$来求解。
首先，将$34.64$转化为与$0.03464$相似的形式，即$34.64 = 0.03464 × 1000$。
然后，由于$\sqrt{2m} = 0.03464 × 1000$，可以得到$2m = (0.03464 × 1000)^2 = 0.0012 × 1000000 = 1200$。
最后，解出$m = \frac{1200}{2} = 600$。
【答案】：
(1) $x = 0.1$；$y = 10$
(2) ① $0.245$；② $m = 600$