《2025年初中必刷题八年级数学上册北师大版》

1DPSK原创新素材2025年2月17日,《哪吒之魔童闹海》成为中国首部进入全球影史票房榜前十的电影.如图是某影院部分座位平面示意图,若座位A的坐标为$(3,2)$,座位B的坐标为$(-1,1)$,则座位C的坐标为( )

A.$(1,4)$
B.$(4,1)$
C.$(0,3)$
D.$(3,0)$

答案：
A 【解析】由A,B坐标可建立如图所示的平面直角坐标系,则C的坐标为(1,4).故选A.

2[2025辽宁丹东期中]若点$A(-3,a)$在x轴上,则点$B(a-1,a+2)$在( )

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： B 【解析】因为点A(-3,a)在x轴上,所以a=0,所以a - 1=-1,a+2=2,所以点B(a - 1,a+2)在第二象限.故选B.

3[2025河南安阳期末]如图,在$\triangle ABC$中,点A的坐标为$(0,1)$,点B的坐标为$(0,4)$,点C的坐标为$(4,3)$,平面内有一点D,使$\triangle ABD与\triangle ABC$全等,则点D的坐标为( )

A.$(-4,3)$
B.$(-4,2)$
C.$(-4,2)或(-4,3)$
D.$(4,2)或(-4,2)或(-4,3)$

答案：
D 【解析】如图,作直线y=2和直线y=3分别与y轴交于点G,H,当△ABD₁≌△ABC时,△ABD₁和△ABC关于y轴对称,所以点D₁的坐标为(-4,3);当△ABD₂≌△BAC时,CH=D₂G=4,所以点D₂的坐标为(-4,2);当△ABD₃≌△BAC时,CH=D₃G=4,所以点D₃的坐标为(4,2).综上可知,点D的坐标为(4,2)或(-4,2)或(-4,3),故选D.

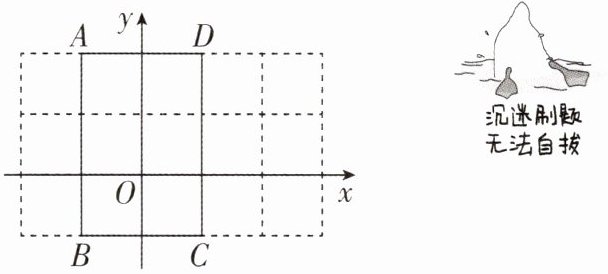
4[2025安徽合肥期中]如图,平面直角坐标系中长方形ABCD的四个顶点坐标分别为$A(-1,2),B(-1,-1),C(1,-1),D(1,2)$,点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个单位长度,同时点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个单位长度,记P,Q在长方形边上第1次相遇时的点为$M_{1}$,第二次相遇时的点为$M_{2}$,第三次相遇时的点为$M_{3}$,…,则点$M_{2025}$的坐标为( )

A.$(1,0)$
B.$(1,2)$
C.$(-1,2)$
D.$(0,-1)$

答案： C 【解析】因为长方形ABCD的四个顶点坐标分别为A(-1,2),B(-1,-1),C(1,-1),D(1,2),所以AB=CD=2 - (-1)=3,AD=BC=1 - (-1)=2,所以长方形的周长为(3+2)×2=10.设经过t秒P,Q第一次相遇,则P点走的路程为2t,Q点走的路程为3t,根据题意得2t+3t=10,解得t=2,所以当t=2时,P,Q第一次相遇,此时相遇点M₁的坐标为(1,0);易得当t=4时,P,Q第二次相遇,此时相遇点M₂的坐标为(-1,0);当t=6时,P,Q第三次相遇,此时相遇点M₃的坐标为(1,2);当t=8时,P,Q第四次相遇,此时相遇点M₄的坐标为(0,-1);当t=10时,P,Q第五次相遇,此时相遇点M₅的坐标为(-1,2);当t=12时,P,Q第六次相遇,此时相遇点M₆的坐标为(1,0),所以五次相遇为一循环.又因为2025÷5=405,所以点M₂₀₂₅的坐标为(-1,2).故选C.

5在平面直角坐标系中,若点$A(a-1,b+1)和B(-3,a-3)关于直线x= 1$对称,则$a+b= $____.

答案： 8 【解析】因为点A(a - 1,b+1)和B(-3,a - 3)关于直线x=1对称,所以$\frac{a - 1 - 3}{2}$=1,b+1=a - 3,解得a=6,b=2,则a+b=6+2=8.

6[2025陕西榆林期中]点$A(a,b)$到x轴的距离是5,到y轴的距离是6,且$a\lt b$,则点A的坐标为____.

答案： (-6,5)或(-6,-5) 【解析】因为点A(a,b)到x轴的距离是5,到y轴的距离是6,所以|b|=5,|a|=6,所以a=±6,b=±5.因为a＜b,所以a=-6,b=5或a=-6,b=-5,所以点A的坐标为(-6,5)或(-6,-5),故答案为(-6,5)或(-6,-5).关键点拨正确理解题目中对“a级关联点”的定义是解决此题的关键.

三、解答题(共40分)
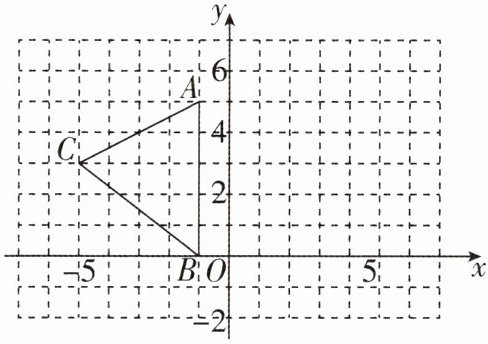
7如图,在平面直角坐标系中,$\triangle ABC的顶点坐标为A(-1,5),B(-1,0),C(-5,3)$.
(1)请在图中画出$\triangle ABC$关于y轴对称的图形$\triangle A_{1}B_{1}C_{1}$(其中$A_{1},B_{1},C_{1}$分别是A,B,C的对应点,不写画法);
(2)直接写出$A_{1},B_{1},C_{1}$三点的坐标:$A_{1}$( , ),$B_{1}$( , ),$C_{1}$( , ).

答案：

(1)如图所示,△A₁B₁C₁即为所求.

(2)根据
(1)的图形可知A₁(1,5),B₁(1,0),C₁(5,3).故答案为1,5,1,0,5,3.

8[2024江西宜春调研]在平面直角坐标系xOy中,对于点$P(x,y)$,若点Q的坐标为$(ax+y,x+ay)$,则称点Q是点P的“a级关联点”(其中a为常数,且$a≠0$),例如,点$P(1,4)$的“2级关联点”为$Q(2×1+4,1+2×4)$,即$Q(6,9)$.
(1)若点P的坐标为$(-1,3)$,则它的“1级关联点”的坐标为____;
(2)若点Q是点$P(m-2,3m)$的“-2级关联点”,且点Q位于坐标轴上,求m的值.

答案：
(1)若点P的坐标为(-1,3),则它的“1级关联点”的坐标为(1×(-1)+3,-1+1×3),即(2,2).故答案为(2,2).
(2)点P(m - 2,3m)的“-2级关联点”为Q(-2(m - 2)+3m,m - 2+(-2)×3m),即(m+4,-5m - 2).
①Q位于x轴上时,-5m - 2=0,解得m=-$\frac{2}{5}$;
②Q位于y轴上时,m+4=0,解得m=-4.
综上所述,m的值为-$\frac{2}{5}$或-4.