《2025年初中必刷题八年级数学上册北师大版》

1 [2024四川甘孜州中考]在平面直角坐标系中,一次函数$y = x + 1$的图象不经过的象限为( )

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： 1.D　[解析]在y=x+1中,k=1＞0,b=1＞0,所以图象经过第一、二、三象限，不经过第四象限,故选D.

2 [2024内蒙古通辽中考]如图,在同一平面直角坐标系中,一次函数$y = k_{1}x + b_{1}与y = k_{2}x + b_{2}$(其中$k_{1}k_{2} \neq 0$,$k_{1}$,$k_{2}$,$b_{1}$,$b_{2}$为常数)的图象分别为直线$l_{1}$,$l_{2}$. 下列结论正确的是 ( )

A.$b_{1} + b_{2} ＞ 0$
B.$b_{1}b_{2} ＞ 0$
C.$k_{1} + k_{2} ＜ 0$
D.$k_{1}k_{2} ＜ 0$

答案： 2.A　[解析]由图象可得k₁＞0,b₁=2,k₂＞0,b₂=−1,所以b₁+b₂＞0,b₁b₂＜0,k₁+k₂＞0,k₁k₂＞0,所以A选项符合题意，故选A.

3 [广西柳州中考]如图,直线$y_{1} = x + 3分别与x$轴、$y轴交于点A和点C$,直线$y_{2} = - x + 3分别与x$轴、$y轴交于点B和点C$,点$P(m,2)是\triangle ABC$内部(包括边上)的一点,则$m$的最大值与最小值之差为( )

A.1
B.2
C.4
D.6

答案：
3.B　[解析]因为点P(m,2)是△ABC内部(包括边上)的一点,所以点P在直线y=2上,如图所示.当P为直线y=2与直线y₂的交点时,m取最大值,当P为直线y=2与直线y₁的交点时,m取最小值.因为在y₂=−x+3中,令y=2,则x=1,在y₁=x+3中，令y=2,则x=−1,所以m的最大值为1，最小值为−1.故m的最大值与最小值之差为1−(−1)=2.故选B.
　　　　

4 [2024江苏镇江中考]点$A(1,y_{1})$,$B(2,y_{2})在一次函数y = 3x + 1$的图象上,则$y_{1}$______$y_{2}$.(用“＜”“ = ”或“＞”填空)

答案： 4.＜　[解析]在一次函数y=3x+1中,k=3＞0,所以y随着x的增大而增大.因为1＜2，所以y₁＜y₂.故答案为＜.

5 [2024江苏扬州中考]如图,已知一次函数$y = kx + b(k \neq 0)的图象分别与x$,$y轴交于A$,$B$两点,若$OA = 2$,$OB = 1$,则关于$x的方程kx + b = 0$的解为______.

答案： 5.x=−2　[解析]因为一次函数y=kx+b(k≠0)的图象与x轴交于点A，且OA=2,所以结合图象可知A(−2,0),所以关于x的方程kx+b=0的解为x=−2,故答案为x=−2.

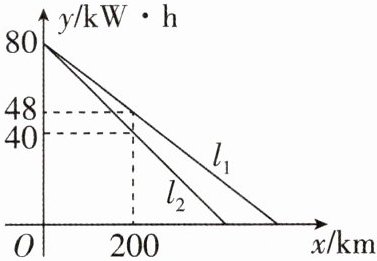
6 [2024山东济南中考]某公司生产了$A$,$B$两款新能源电动汽车.如图,$l_{1}$,$l_{2}分别表示A$款,$B款新能源电动汽车充满电后电池的剩余电量y(\text{kW}\cdot\text{h})与汽车行驶路程x(\text{km})$的关系. 当两款新能源电动汽车的行驶路程都是$300\text{km}$时,$A款新能源电动汽车电池的剩余电量比B$款新能源电动汽车电池的剩余电量多______$\text{kW}\cdot\text{h}$.

答案： 6.12　[解析]设直线l₁的函数表达式为y₁=ax+b,直线l₂的函数表达式为y₂=kx+c.将思路分析 分别求出l₁,l₂的函数表达式,将x=300分别代入,求出对应的函数值并计算二者之差即可.关键点拨 关键要理解当P在何处时m存在最大值与最小值,由于P的纵坐标为2,故作出直线y=2有助于判断P的位置.(0,80),(200,48)代入y₁=ax+b,解得a=−0.16,b=80.将(0,80),(200,40)代入y₂=kx+c,解得k=−0.2,c=80,所以l₁的函数表达式为y₁=80−0.16x,l₂的函数表达式为y₂=80−0.2x.当x=300时,y₁=80−0.16×300=32,y₂=80−0.2×300=20,32−20=12(kW·h),所以当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多12kW·h.故答案为12.

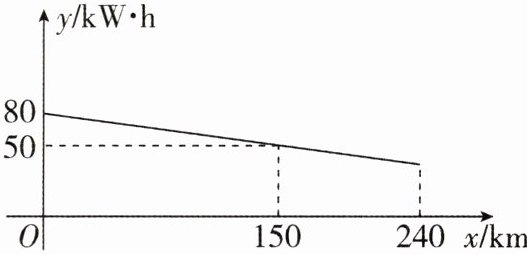
7 [2024陕西中考]我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从$A市前往B$市. 他驾车从$A$市一高速公路入口驶入时,该车的剩余电量是$80\text{kW}\cdot\text{h}$,行驶了$240\text{km}$后,从$B$市一高速公路出口驶出. 已知该车在高速公路上行驶的过程中,剩余电量$y(\text{kW}\cdot\text{h})与行驶路程x(\text{km})$之间的关系如图所示.
(1)求$y与x$之间的关系式；
(2)已知这辆车的“满电量”为$100\text{kW}\cdot\text{h}$,求王师傅驾车从$B$市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少.

答案： 7.[解]
(1)设y与x之间的关系式为y=kx+b.将(0,80),(150,50)代入得80=b,50=150k+b,解得k=−0.2,b=80,所以y与x之间的关系式为y=−0.2x+80.
(2)当x=240时,y=−0.2×240+80=32,$\frac{32}{100}$×100%=32%.
答:该车的剩余电量占“满电量”的32%