《2025年初中必刷题八年级数学上册北师大版》

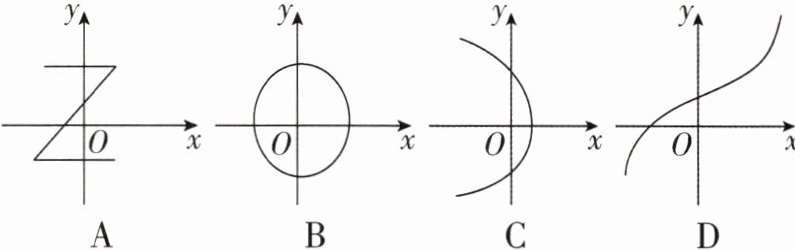
1 下列平面直角坐标系中的曲线或折线中,能表示 $ y $ 是 $ x $ 的函数的是 ( )

答案： D 【解析】选项 A、B、C 中存在一个 x 值，与之对应的 y 值不是唯一的，所以选项 A、B、C 不能表示 y 是 x 的函数；D 选项中任意一个 x 值，总有唯一的 y 值与之对应，所以 D 选项可以表示 y 是 x 的函数，故 D 选项符合题意.

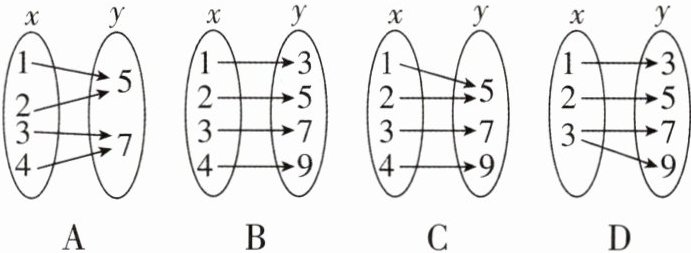
2 [2025 江苏南京质检]下列关于变量 $ x $,$ y $ 的关系中,$ y $ 不是 $ x $ 的函数的是 ( )

答案： D 【解析】根据函数定义可知，对于变量 x 的每一个确定的值，变量 y 都有唯一确定的值与之对应，所以 D 选项不符合题意. 故选 D.

3 [2025 河北唐山期中]变量 $ x $,$ y $ 有如下关系：①$ 3 x - 2 y = 0 $；②$ y = 3 x ^ { 2 } $；③$ y ^ { 2 } = 8 x $；④$ y = \sqrt { x } $；⑤$ y = | x | $；⑥$ | y | = x $.其中 $ y $ 是 $ x $ 的函数的是______.(填序号)

答案： ①②④⑤ 【解析】①3x-2y=0，②y=3x²，④y=√x，⑤y=|x|，对于 x 的每一个值，y 都有唯一的值与它对应，符合函数的定义；③y²=8x，⑥|y|=x，对于 x 的每一个值，y 不是有唯一的值与它对应，不符合函数的定义. 故答案为①②④⑤.

4 [2025 广东清远期末]一支签字笔的单价为 $ 2.5 $ 元,小涵同学拿了 $ 50 $ 元钱去购买了 $ x ( x \leq 20 ) $ 支该型号的签字笔,则剩余的钱 $ y $ 与 $ x $ 之间的关系式是 ( )

A.$ y = 2.5 x $
B.$ y = 50 - 2.5 x $
C.$ y = 2.5 x - 50 $
D.$ y = 50 + 2.5 x $

答案： B 【解析】y 与 x 之间的关系式是y=50-2.5x. 故选 B.

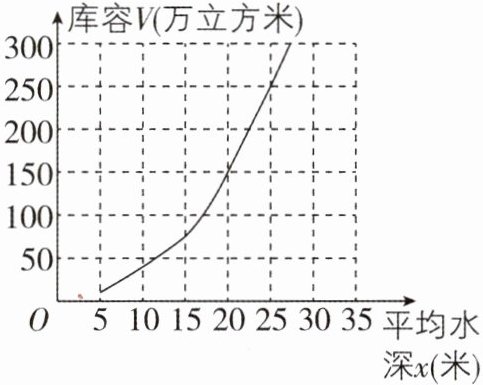
5 [2025 浙江温州调研]如图是某水库的平均水深 $ x $(米)与库容 $ V $(万立方米)之间的关系图象.根据图象回答下面的问题：
(1)将表格填写完整：
| $ x $(米) | $ 5 $ | $ 10 $ | $ 15 $ | $ 20 $ | $ 25 $ |
| $ V $(万立方米) | $ 10 $ | $ 40 $ | $ 75 $ | | |
(2)当平均水深 $ x $ 取 $ 5 $ 米至 $ 25 $ 米之间的一个确定的值时,相应的库容 $ V $ 唯一确定吗？
(3)库容 $ V $ 可以看成平均水深 $ x $ 的函数吗？

答案： 【解】
(1)从左到右依次填入 150,250.
(2)当平均水深 x 取 5 米至 25 米之间的一个确定的值时，相应的库容 V 唯一确定.
(3)库容 V 可以看成平均水深 x 的函数.

6 [2025 重庆沙坪坝区校级期中]函数 $ y = \sqrt { x - 3 } + 1 $ 的自变量 $ x $ 的取值范围是 ( )

A.$ x ＜ 3 $
B.$ x ＞ 3 $
C.$ x \leq 3 $
D.$ x \geq 3 $

答案： D 【解析】根据二次根式有意义的条件可知x-3≥0，则x≥3$,$所以自变量 x 的取值范围是x≥3. 故选 D.

7 [2024 河北石家庄质检]按照如图所示的运算程序计算函数 $ y $ 的值,若输入 $ x $ 的值是 $ 5 $,则输出 $ y $ 的值是 $ 14 $,若输入 $ x $ 的值是 $ - 4 $,则输出 $ y $ 的值是______.

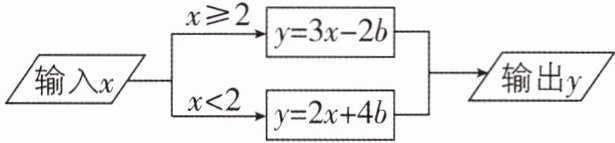
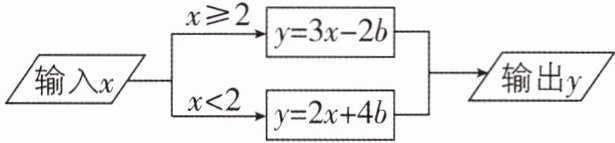
答案： 【解析】：
本题可先根据输入$x$的值是$5$，结合运算程序确定对应的函数表达式，进而求出$b$的值，再将$x = - 4$代入相应的函数表达式求出$y$的值。
步骤一：根据$x = 5$求出$b$的值
已知运算程序中，当$x\geq2$时，$y = 3x - 2b$；当$x\lt2$时，$y = 2x + 4b$。
因为$5\gt2$，所以将$x = 5$代入$y = 3x - 2b$中，可得$y = 3×5 - 2b=15 - 2b$。
又因为输入$x$的值是$5$时，输出$y$的值是$14$，所以$15 - 2b = 14$，解方程：
$\begin{align}15 - 2b &= 14\\-2b &= 14 - 15\\-2b &= -1\\b&=\frac{1}{2}\end{align}$
步骤二：根据$b$的值和$x = - 4$求出$y$的值
因为$-4\lt2$，所以将$x = - 4$代入$y = 2x + 4b$中，又因为$b = \frac{1}{2}$，则可得：
$\begin{align}y&=2×(-4)+4×\frac{1}{2}\\&=-8 + 2\\&=-6\end{align}$
【答案】：$-6$

8 [2025 浙江温州质检]已知三角形的周长为 $ y \mathrm { ~cm } $,三边长分别为 $ 9 \mathrm { ~cm } $,$ 5 \mathrm { ~cm } $,$ x \mathrm { ~cm } $.
(1)求 $ y $ 与 $ x $ 之间的关系式及其自变量 $ x $ 的取值范围.
(2)当 $ x = 6 $ 时,求 $ y $ 的值.
(3)当 $ y = 19.5 $ 时,求 $ x $ 的值.

答案： 【解】
(1)由三角形的周长公式$,$得y=x+14. 由三角形的三边关系$,$得4＜x＜14.
(2)当x=6时$,$y=6+14=20.
(3)当y=19.5时$,$x+14=19.5$,$所以x=5.5.