《2025年初中必刷题八年级数学上册北师大版》

1[2025江苏盐城期末]若一次函数$y=kx+b$的图象经过点$A(2,0)$，点$B(0,-3)$，则该函数图象不经过的象限是（ ）

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案：
B　[解析]在平面直角坐标系中描出点A(2,0),B(0,−3),画出此一次函数图象，如图所示，所以该函数图象不经过第二象限.故选B.

2[2024湖南岳阳调研]如图所示的图象中，可能是一次函数$y=-ax+a(a≠0)$的图象的是（ ）

答案： B　[解析]当a＞0时,一次函数y=−ax+a(a≠0)的图象经过第一、二、四象限;当a＜0 时,一次函数y=−ax+a(a≠0)的图象经过第一、三、四象限，故选项B符合题意.故选B.

3已知点$P(m,n)$在一次函数$y=2x-3$的图象上，则$2m-n-3$的值是____。

答案： 0　[解析]因为P(m,n)在一次函数y=2x−3的图象上,所以n=2m−3,所以2m−n−3=0,故答案为0.

4[2025陕西西安质检]将表格补充完整，并根据表中的数据在如图所示的平面直角坐标系中画出一次函数$y=2x-6$的图象。
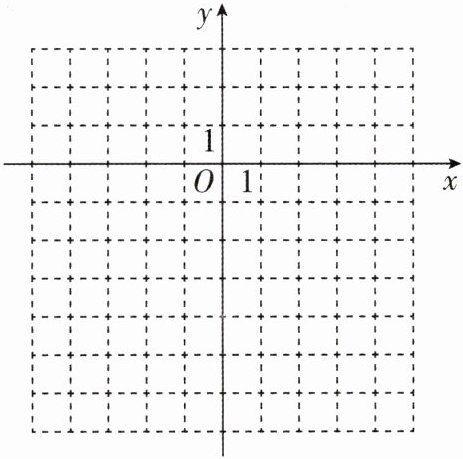
(1)列表：
|$x$|0| |
|----|----|----|
|$y=2x-6$| |0|
(2)描点、连线，画出一次函数$y=2x-6$的图象。

答案：
[解]
(1)将x=0代入y=2x−6,得y=−6;将y=0代入y=2x−6,得2x−6=0,解得x=3.故答案从左到右为−6,3.
(2)一次函数y=2x−6的图象如图所示.

5[2025浙江台州质检]关于函数$y=-x+1$的图象与性质，下列说法错误的是（ ）

A.图象不经过第三象限
B.当$-2≤x≤1$时，函数值$y$有最小值3
C.$y$随$x$的增大而减小
D.图象是与直线$y=-x-1$平行的一条直线

答案： B　[解析]因为y=−x+1,k=−1＜0,b=1＞0,所以该函数图象经过第一、二、四象限，不经过第三象限，故A选项正确，不符合题意;因为k=−1＜0,所以y随x的增大而减小,所以当−2≤x≤1时,函数y有最小值,为−1+1=0,故B选项错误，符合题意，C选项正确，不符合题意;y=−x+1与y=−x−1的k值都为−1,所以y=−x+1的图象是与直线y=−x−1平行的一条直线，故D选项正确，不符合题意.故选B.

6[2024河北保定莲池区期末]若点$A(x_{1},-1)$，$B(x_{2},-2)$，$C(x_{3},3)$在一次函数$y=-2x+m$（$m$是常数）的图象上，则$x_{1}$，$x_{2}$，$x_{3}$的大小关系是（ ）

A.$x_{1}＞x_{2}＞x_{3}$
B.$x_{2}＞x_{1}＞x_{3}$
C.$x_{1}＞x_{3}＞x_{2}$
D.$x_{3}＞x_{2}＞x_{1}$

答案： B　[解析]因为一次函数y=−2x+m(m是常数)中,−2＜0,所以y随x的增大而减小.因为A(x₁,−1),B(x₂,−2),C(x₃,3)在一次函数y=−2x+m(m是常数)的图象上,其中−2＜−1＜3,所以x₂＞x₁＞x₃,故选B.

7[2024江西南昌期末]一次函数$y=mx+|m-1|$的图象过点$(0,2)$，且$y$随$x$的增大而减小，则$m=$____。

答案： −1　[解析]因为一次函数y=mx+|m - 1|的图象过点(0,2),所以|m - 1|=2,解得m=3或−1.因为y随x的增大而减小,所以m＜0,所以m=−1,故答案为−1.

8[2024广东广州天河区质检]当$1≤x≤10$时，一次函数$y=-3x+b$的最大值为17，则$b=$____。

答案： 20　[解析]在一次函数y=−3x+b中,−3＜0,所以y随着x的增大而减小.因为当1≤x≤10时，一次函数y=−3x+b取得最大值17,所以x=1时,y=−3x+b=17,所以−3+b=17,解得b=20,故答案为20.

9[2023江苏无锡中考]将函数$y=2x+1$的图象向下平移2个单位长度，所得图象对应的函数表达式是（ ）

A.$y=2x-1$
B.$y=2x+3$
C.$y=4x-3$
D.$y=4x+5$

答案： A　[解析]将函数y=2x+1的图象向下平移2个单位长度,所得函数图象的表达式是y=2x+1−2=2x−1,故选A.

10[2025江苏南京期末]将一次函数$y=x-2$的图象向上平移$m$个单位长度后经过点$(1,4)$，则$m$的值为（ ）

A.6
B.5
C.-5
D.-6

答案： B　[解析]因为将一次函数y=x−2的图象向上平移m个单位长度,所以平移后图象对应的表达式为y=x−2+m.因为平移后的图象经过点(1,4),所以4=1−2+m,解得m=5.故选B.

11[2025安徽亳州校级期末]一次函数$y=2x+b$图象向上平移3个单位后经过原点，则$b=$____。

答案： −3　[解析]直线y=2x+b向上平移3个单位后对应的表达式为y=2x+b+3.因为平移后的直线经过原点(0,0),所以2×0+b+3=0,解得b=−3.故答案为−3.