第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1 [2025 北京朝阳区校级期中]如图,飞机在空中展示的队形是轴对称图形,以飞机 B,C 所在直线为 x 轴、队形的对称轴为 y 轴,建立平面直角坐标系.若飞机 E 的坐标为(50,m),则飞机 D 的坐标为 ( )
A.(-50,m)
B.(50,-m)
C.(-50,-m)
D.(m,-50)
A.(-50,m)
B.(50,-m)
C.(-50,-m)
D.(m,-50)
答案:
A [解析]因为飞机E(50,m)与飞机D关于y轴对称,所以飞机D的坐标为(−50,m).故选A.
2 [2024 广西柳州城中区质检]如图,在平面直角坐标系中,△ABC 关于直线 m(直线 m 上各点的横坐标都为 1)对称,点 C 的坐标为(4,1),则点 B 的坐标为 ( )
A.(-2,1)
B.(-3,1)
C.(-2,-1)
D.(2,1)
A.(-2,1)
B.(-3,1)
C.(-2,-1)
D.(2,1)
答案:
A [解析]因为△ABC关于直线m(直线m上各点的横坐标都为1)对称,所以C,B关于直线m对称,即关于直线x = 1对称.设点B的坐标为(x,1).因为点C的坐标为(4,1),所以$\frac{4 + x}{2}=1$,解得x = −2,则点B的坐标为(−2,1).故选A.
3 [2025 山东青岛调研]在平面直角坐标系中,点 A(-1,4)和 B(-1,-4)关于____对称.(填“x 轴”或“y 轴”)
答案:
x轴 [解析]点A(−1,4)和B(−1,−4)关于x轴对称.故答案为x轴.
4 [2024 广东深圳期中]如图,一只跳蚤从 M 点出发,先向上爬了 2 个单位,又向左爬了 3 个单位到达 P 点,然后跳到点 P 关于 x 轴对称的点$ P_1,$则点$ P_1 $的坐标为____.


答案:
(−3,−3) [解析]由题图知M(0,1),一只跳蚤从M点出发,先向上爬了2个单位,又向左爬了3个单位到达P点,所以点P的坐标为(−3,3).因为点P与点P₁关于x轴对称,所以P₁的坐标为(−3,−3),故答案为(−3,−3).
5 已知在 Rt△ABC 中,∠C = 90°,AC = 3,BC = 4,在如图的平面直角坐标系中,点 A 的坐标为(0,1),点 B 的坐标为(-3,5),AC 与 x 轴平行.
(1)求点 C 的坐标;
(2)在如图的平面直角坐标系中作出△ABC 关于 y 轴对称的$△A_1B_1C_1,$并在图中标出$ B_1,C_1 $两点的坐标;
(3)若$△A_2B_2C_2 $与△ABC 关于 x 轴对称,求$△A_2B_2C_2 $各顶点的坐标.
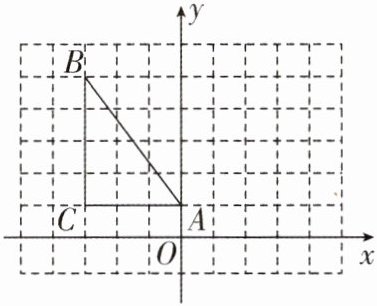
(1)求点 C 的坐标;
(2)在如图的平面直角坐标系中作出△ABC 关于 y 轴对称的$△A_1B_1C_1,$并在图中标出$ B_1,C_1 $两点的坐标;
(3)若$△A_2B_2C_2 $与△ABC 关于 x 轴对称,求$△A_2B_2C_2 $各顶点的坐标.

答案:
[解]
(1)由题图可知,点C的坐标为(−3,1).
(2)如图所示,△A₁B₁C₁即为所作.

关键点拨:OA与AB的长度大小关系不确定,需要分类讨论,这是解决此题的突破口。
归纳总结:关于坐标轴对称的点的坐标特征:关于x轴对称,横不变纵相反;关于y轴对称,纵不变横相反。
关键点拨:轴对称图形上对应点的连线被对称轴垂直平分。
(3)A₂(0,−1),B₂(−3,−5),C₂(−3,−1).
[解]
(1)由题图可知,点C的坐标为(−3,1).
(2)如图所示,△A₁B₁C₁即为所作.

关键点拨:OA与AB的长度大小关系不确定,需要分类讨论,这是解决此题的突破口。
归纳总结:关于坐标轴对称的点的坐标特征:关于x轴对称,横不变纵相反;关于y轴对称,纵不变横相反。
关键点拨:轴对称图形上对应点的连线被对称轴垂直平分。
(3)A₂(0,−1),B₂(−3,−5),C₂(−3,−1).
6 [2024 安徽宣城宣州区质检]佳佳将平面直角坐标系中一图案横向拉长为原来的 2 倍,又向右平移 2 个单位,若想变回原来的图案,需要变化后的图案上各点坐标 ( )

A.纵坐标不变,横坐标减 2
B.纵坐标不变,横坐标先除以 2,再均减 2
C.纵坐标不变,横坐标除以 2
D.纵坐标不变,横坐标先减 2,再均除以 2

A.纵坐标不变,横坐标减 2
B.纵坐标不变,横坐标先除以 2,再均减 2
C.纵坐标不变,横坐标除以 2
D.纵坐标不变,横坐标先减 2,再均除以 2
答案:
D [解析]因为图案向右平移2个单位,所以想变回原来的图案要先向左平移2个单位,即横坐标先减2.因为图案横向拉长为原来的2倍,所以是横坐标乘2,纵坐标不变,所以想变回原来的图案,要纵坐标不变,横坐标除以2,故选D.
7 [2024 河北承德期中]三角形 ABC 为等腰直角三角形,其中∠A = 90°,BC 长为 6.
(1)建立适当的平面直角坐标系,并写出各个顶点的坐标.
(2)将(1)中各顶点的横坐标保持不变,纵坐标都乘 -1,与原图形相比,所得的图形有什么变化?
(3)将(1)中各顶点的横坐标都乘 2,纵坐标保持不变,与原图形相比,所得的图形有什么变化?
(1)建立适当的平面直角坐标系,并写出各个顶点的坐标.
(2)将(1)中各顶点的横坐标保持不变,纵坐标都乘 -1,与原图形相比,所得的图形有什么变化?
(3)将(1)中各顶点的横坐标都乘 2,纵坐标保持不变,与原图形相比,所得的图形有什么变化?
答案:
[解]
(1)以BC边中点O为原点,BC边所在的直线为x轴,BC边的垂直平分线为y轴,建立平面直角坐标系,如图.易知△ABO和△AOC是等腰直角三角形,所以AO = BO = CO = 3,所以A(0,3),B(−3,0),C(3,0).(建系方法不唯一,对应答案不唯一)
(2)与原图形关于x轴对称,如图中的△A₂BC.
(3)与原图形相比,所得的图形横向拉长为原来的2倍,如图中的△AB₃C₃.

[解]
(1)以BC边中点O为原点,BC边所在的直线为x轴,BC边的垂直平分线为y轴,建立平面直角坐标系,如图.易知△ABO和△AOC是等腰直角三角形,所以AO = BO = CO = 3,所以A(0,3),B(−3,0),C(3,0).(建系方法不唯一,对应答案不唯一)
(2)与原图形关于x轴对称,如图中的△A₂BC.
(3)与原图形相比,所得的图形横向拉长为原来的2倍,如图中的△AB₃C₃.

查看更多完整答案,请扫码查看


