2025年诚成教育学业评价九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年诚成教育学业评价九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
三、解答题(共60分)
21.(6分)已知二次函数y=x²+mx+m²−3(m为常数,m>0)的图象经
过点P(2,4).
(1)求m的值;
(2)判断二次函数y=x²+mx+m²−3的图象与x轴交点的个数,并说明理由.
21.(6分)已知二次函数y=x²+mx+m²−3(m为常数,m>0)的图象经
过点P(2,4).
(1)求m的值;
(2)判断二次函数y=x²+mx+m²−3的图象与x轴交点的个数,并说明理由.
答案:
解:
(1)将点P(2,4)代入y = x² + mx + m² - 3,得4 = 4 + 2m + m² - 3.
解得m₁ = 1,m₂ = - 3.
又m>0,
∴m = 1.
(2)交点个数为2.
理由:
∵m = 1,
∴y = x² + x - 2.
∵1² - 4×1×(-2) = 9>0,
∴二次函数图象与x轴有2个交点.
(1)将点P(2,4)代入y = x² + mx + m² - 3,得4 = 4 + 2m + m² - 3.
解得m₁ = 1,m₂ = - 3.
又m>0,
∴m = 1.
(2)交点个数为2.
理由:
∵m = 1,
∴y = x² + x - 2.
∵1² - 4×1×(-2) = 9>0,
∴二次函数图象与x轴有2个交点.
22.(6分)如图是二次函数y=(x+2)²的图象,顶点为A,与y轴的交点为B.
(1)求经过A,B两点的直线的函数关系式;
(2)在第二象限中的抛物线上存在一点C,使△ABC的面积与△ABO的面积相等,请直接写出点C的坐标.
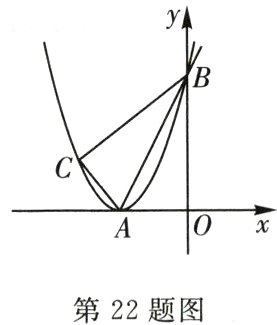
(1)求经过A,B两点的直线的函数关系式;
(2)在第二象限中的抛物线上存在一点C,使△ABC的面积与△ABO的面积相等,请直接写出点C的坐标.

答案:
解:
(1)令x = 0,则y = 2² = 4.
∴B(0,4).
令y = 0,则(x + 2)² = 0.
∴x₁ = x₂ = - 2.
∴A(-2,0).
设过A,B两点的直线的函数关系式为y = kx + b.
由题意,得{0 = - 2k + b,4 = b.
解得{b = 4,k = 2.
∴经过A,B两点的直线的函数关系式为y = 2x + 4.
(2)C(-1 - √5,6 - 2√5).
(1)令x = 0,则y = 2² = 4.
∴B(0,4).
令y = 0,则(x + 2)² = 0.
∴x₁ = x₂ = - 2.
∴A(-2,0).
设过A,B两点的直线的函数关系式为y = kx + b.
由题意,得{0 = - 2k + b,4 = b.
解得{b = 4,k = 2.
∴经过A,B两点的直线的函数关系式为y = 2x + 4.
(2)C(-1 - √5,6 - 2√5).
23.(6分)在平面直角坐标系中已知抛物线 =ax²+bx−4经过A(−4,0),C(2,0)两点,与y 轴交于点B.
(1)求抛物线的解析式:
(2)若M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值
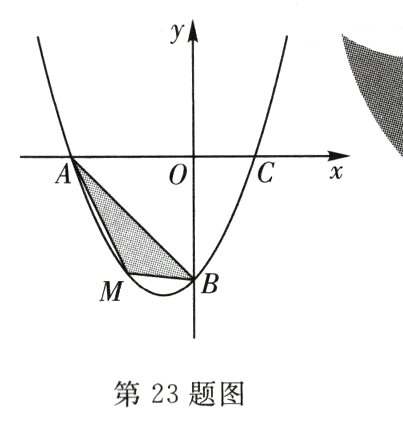
(1)求抛物线的解析式:
(2)若M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S,求S关于m的函数关系式,并求出S的最大值

答案:
解:
(1)把点A(-4,0),C(2,0)代入y = ax² + bx - 4,
得{16a - 4b - 4 = 0,4a + 2b - 4 = 0.
解得{a = 1/2,b = 1.
∴抛物线的解析式为y = 1/2x² + x - 4.
(2)如图,过点M作MN⊥AC,垂足为N,
则四边形OBMN为梯形.
易得抛物线y = 1/2x² + x - 4与y轴的交点B的坐标为(0,- 4),点M的坐标为(m,1/2m² + m - 4)(-4<m<0).
∴ON = - m,MN = - 1/2m² - m + 4,
AN = 4 - (- m) = 4 + m,OB = 4.
∴S = S△ANM + S梯形MNOB - S△AOB
= 1/2(4 + m)(- 1/2m² - m + 4) +
1/2(- 1/2m² - m + 4 + 4)(- m) -
1/2×4×4
= - m² - 4m
= -(m + 2)² + 4.
∴当m = - 2时,S取得最大值,最大值为4.
∴S关于m的函数关系式为S = - m² - 4m,S的最大值为4.
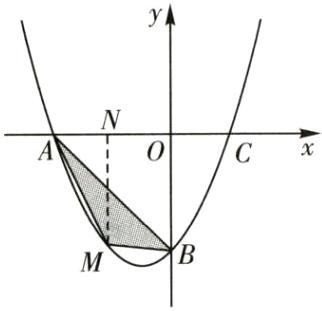
解:
(1)把点A(-4,0),C(2,0)代入y = ax² + bx - 4,
得{16a - 4b - 4 = 0,4a + 2b - 4 = 0.
解得{a = 1/2,b = 1.
∴抛物线的解析式为y = 1/2x² + x - 4.
(2)如图,过点M作MN⊥AC,垂足为N,
则四边形OBMN为梯形.
易得抛物线y = 1/2x² + x - 4与y轴的交点B的坐标为(0,- 4),点M的坐标为(m,1/2m² + m - 4)(-4<m<0).
∴ON = - m,MN = - 1/2m² - m + 4,
AN = 4 - (- m) = 4 + m,OB = 4.
∴S = S△ANM + S梯形MNOB - S△AOB
= 1/2(4 + m)(- 1/2m² - m + 4) +
1/2(- 1/2m² - m + 4 + 4)(- m) -
1/2×4×4
= - m² - 4m
= -(m + 2)² + 4.
∴当m = - 2时,S取得最大值,最大值为4.
∴S关于m的函数关系式为S = - m² - 4m,S的最大值为4.

24.(6分)某商人将每件进价为8元的纪念品,按每件9元出售,每天可售出20件.他想采用提高售价的办法来增加利润,经试验,发现这种纪品每件提价元每天的销售量会少4件.


答案:
解:
(1)由题意,得
y = (x - 8)[20 - 4(x - 9)].
即y = - 4x² + 88x - 448.
(2)y = - 4x² + 88x - 448
= - 4(x - 11)² + 36.
当x = 11时,y最大,为36.
即每件售价定为11元时,才能使一天所得的利润最大,最大利润为36元.
(1)由题意,得
y = (x - 8)[20 - 4(x - 9)].
即y = - 4x² + 88x - 448.
(2)y = - 4x² + 88x - 448
= - 4(x - 11)² + 36.
当x = 11时,y最大,为36.
即每件售价定为11元时,才能使一天所得的利润最大,最大利润为36元.
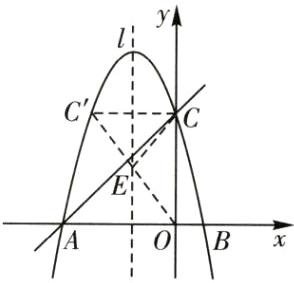
25.(8分)新理念综合探究性试题如图,直线y=x十c与x轴交于点A(−4,0),与y轴交于点C,
抛物线y=-x²+bx+c经过点A,C.
(1)求抛物线的解析式;
(2)点E在抛物线的对称轴上,求CE+OE的最小值.
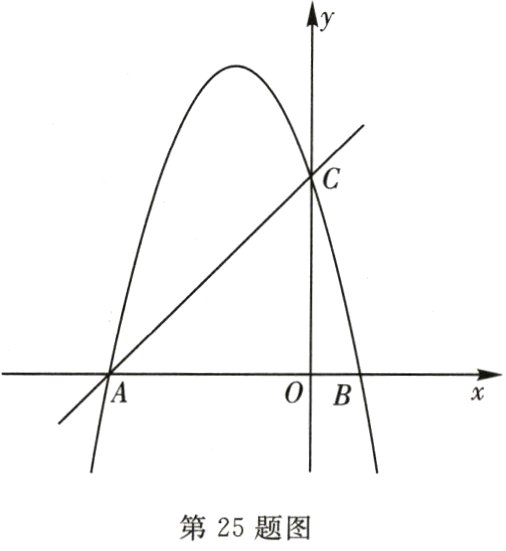
抛物线y=-x²+bx+c经过点A,C.
(1)求抛物线的解析式;
(2)点E在抛物线的对称轴上,求CE+OE的最小值.

答案:
25.解:
(1)将点A(-4,0)代入y = x + c,得c = 4.
将点A(-4,0)和c = 4代入y = - x² + bx + c,得b = - 3.
∴抛物线的解析式为y = - x² - 3x + 4.
(2)如图所示,作点C关于抛物线的对称轴直线l的对称点C',连接OC',交直线l于点E,连接CE,此时CE + OE的值最小.
抛物线的对称轴为
x = -(-3)/(2×(-1)) = - 3/2,
则C'C = 3.由勾股定理,得OC' = 5.
∴CE + OE的最小值为5.
25.解:
(1)将点A(-4,0)代入y = x + c,得c = 4.
将点A(-4,0)和c = 4代入y = - x² + bx + c,得b = - 3.
∴抛物线的解析式为y = - x² - 3x + 4.
(2)如图所示,作点C关于抛物线的对称轴直线l的对称点C',连接OC',交直线l于点E,连接CE,此时CE + OE的值最小.
抛物线的对称轴为
x = -(-3)/(2×(-1)) = - 3/2,
则C'C = 3.由勾股定理,得OC' = 5.
∴CE + OE的最小值为5.


答案:
解:
(1)(80 - 3x).
(2)
∵BC = BG + GC
= 10 + 80 - 3x
= 90 - 3x,
0<BC ≤ 30,
∴0<90 - 3x ≤ 30.即20 ≤ x<30.
∵矩形CDHG的面积为GC·CD,
∴125 = (80 - 3x)x.
解得x = 25或x = 5/3(舍去).
故CD的长为25 m.
(3)设矩形ABCD的面积为S m²,则
S = BC·CD
= (90 - 3x)x
= - 3x² + 90x.
∵ - 3<0,
∴抛物线开口向下.
∴当x> - 90/(2×(-3)) = 15时,S随x的增大而减小.
又20 ≤ x<30,
故当x = 20时,S取得最大值.
即当CD的长为20 m时,矩形ABCD的面积最大.
(1)(80 - 3x).
(2)
∵BC = BG + GC
= 10 + 80 - 3x
= 90 - 3x,
0<BC ≤ 30,
∴0<90 - 3x ≤ 30.即20 ≤ x<30.
∵矩形CDHG的面积为GC·CD,
∴125 = (80 - 3x)x.
解得x = 25或x = 5/3(舍去).
故CD的长为25 m.
(3)设矩形ABCD的面积为S m²,则
S = BC·CD
= (90 - 3x)x
= - 3x² + 90x.
∵ - 3<0,
∴抛物线开口向下.
∴当x> - 90/(2×(-3)) = 15时,S随x的增大而减小.
又20 ≤ x<30,
故当x = 20时,S取得最大值.
即当CD的长为20 m时,矩形ABCD的面积最大.
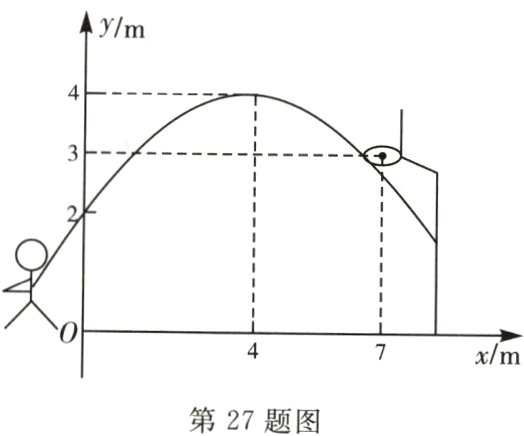
27.如图,在小明的一次篮中,球出手时离地面2米高,与篮筐中心的水平距离为?米,当球出手后水平距离为4米时到达最大高度4米.篮球运行的轨迹为抛物线,篮筐中心距离地面3米,通过计算说明此球能否投至篮筐中心(不考虑篮球大小和篮球的反弹).
探究一:若出手的角度、力度和度都不变 则小明朝着篮球架再向前移动多少米后投篮能将
篮球投至篮筐中心?
探究二:若出手的角度、力度和高度都发生改变但是抛物线的顶点位置及球出手时与篮筐中
心的水平距离不变,则小明 出手的高度需要增加多少米才能将篮球投至篮筐中心?
探究一:若出手的角度、力度和度都不变 则小明朝着篮球架再向前移动多少米后投篮能将
篮球投至篮筐中心?
探究二:若出手的角度、力度和高度都发生改变但是抛物线的顶点位置及球出手时与篮筐中
心的水平距离不变,则小明 出手的高度需要增加多少米才能将篮球投至篮筐中心?

答案:
解:
∵抛物线的顶点坐标为(4,4),
∴设抛物线的表达式为y = a(x - 4)² + 4.
∵抛物线过点(0,2),
∴2 = 16a + 4.
∴a = - 1/8.
∴y = - 1/8(x - 4)² + 4.
当x = 7时,y = - 9/8 + 4 = 23/8 ≠ 3,
∴此球不能投至篮筐中心.
探究一:设向前移动h米.
由题意可得
y = - 1/8(x - 4 - h)² + 4.
代入点(7,3),
得3 = - 1/8(7 - 4 - h)² + 4.
解得h₁ = 3 - 2√2,h₂ = 3 + 2√2(不合题意,舍去).
即向前移动(3 - 2√2)米,可投至篮筐中心.
探究二:设y = m(x - 4)² + 4.
投于篮筐中心,即代入点(7,3),
得3 = m(7 - 4)² + 4.解得m = - 1/9.
∴y = - 1/9(x - 4)² + 4.
当x = 0时,y = 20/9,20/9 - 2 = 2/9.
即小明出手的高度要增加2/9米,可将篮球投至篮筐中心.
∵抛物线的顶点坐标为(4,4),
∴设抛物线的表达式为y = a(x - 4)² + 4.
∵抛物线过点(0,2),
∴2 = 16a + 4.
∴a = - 1/8.
∴y = - 1/8(x - 4)² + 4.
当x = 7时,y = - 9/8 + 4 = 23/8 ≠ 3,
∴此球不能投至篮筐中心.
探究一:设向前移动h米.
由题意可得
y = - 1/8(x - 4 - h)² + 4.
代入点(7,3),
得3 = - 1/8(7 - 4 - h)² + 4.
解得h₁ = 3 - 2√2,h₂ = 3 + 2√2(不合题意,舍去).
即向前移动(3 - 2√2)米,可投至篮筐中心.
探究二:设y = m(x - 4)² + 4.
投于篮筐中心,即代入点(7,3),
得3 = m(7 - 4)² + 4.解得m = - 1/9.
∴y = - 1/9(x - 4)² + 4.
当x = 0时,y = 20/9,20/9 - 2 = 2/9.
即小明出手的高度要增加2/9米,可将篮球投至篮筐中心.
28.(10分)某产品每件成本为25元,经过市场调研发现,这种产品在未来20天内的日销售量m(单位:件)是关于时间t(单位:天)的一次函数,调研所获的部分数据如表:

这20天中,该产品每天的售价y(单位:元/件)与时间t(单位;天)的函数解析式为 =$\frac{1}{4}$t+30(t为正整数). 失的
(1)求m关于t的函数解析式
(2)这20天中哪一天的日销售利润最大?最大日销售利润是多少?
(3)在实际销售的20天中,每销售一件商品就捐赠a元(a<6)给希望工程,通过销售记录发现,这20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.

这20天中,该产品每天的售价y(单位:元/件)与时间t(单位;天)的函数解析式为 =$\frac{1}{4}$t+30(t为正整数). 失的
(1)求m关于t的函数解析式
(2)这20天中哪一天的日销售利润最大?最大日销售利润是多少?
(3)在实际销售的20天中,每销售一件商品就捐赠a元(a<6)给希望工程,通过销售记录发现,这20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
答案:
28.解:
(1)设m = kt + b(k ≠ 0).
将(2,96)和(3,94)代入,得{2k + b = 96,3k + b = 94.
解得{k = - 2,b = 100.
∴m关于t的函数解析式为m = - 2t + 100.
(2)设日销售利润为w元.根据题意,得
w = (1/4t + 30 - 25)(- 2t + 100).
化简,得w = - 1/2t² + 15t + 500.
∵ - 1/2<0,对称轴为
t = - 15/(2×(-1/2)) = 15,
∴当t = 15时,w最大.
此时w = - 1/2×15² + 15×15 + 500
= 612.5.
答:第15天的日销售利润最大,为612.5元.
(3)设每天扣除捐赠后的日销售利润为n元.根据题意,得
n = (1/4t + 30 - 25 - a)(- 2t + 100)
= - 1/2t² + (15 + 2a)t + 100(5 - a).
∴对称轴为t = -(15 + 2a)/(2×(-1/2)) = 15 + 2a.
∵ - 1/2<0,
∴抛物线开口向下.
∵要使每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴15 + 2a ≥ 20,解得a ≥ 2.5.
又a<6,
∴2.5 ≤ a<6.
答:a的取值范围是2.5 ≤ a<6.
(1)设m = kt + b(k ≠ 0).
将(2,96)和(3,94)代入,得{2k + b = 96,3k + b = 94.
解得{k = - 2,b = 100.
∴m关于t的函数解析式为m = - 2t + 100.
(2)设日销售利润为w元.根据题意,得
w = (1/4t + 30 - 25)(- 2t + 100).
化简,得w = - 1/2t² + 15t + 500.
∵ - 1/2<0,对称轴为
t = - 15/(2×(-1/2)) = 15,
∴当t = 15时,w最大.
此时w = - 1/2×15² + 15×15 + 500
= 612.5.
答:第15天的日销售利润最大,为612.5元.
(3)设每天扣除捐赠后的日销售利润为n元.根据题意,得
n = (1/4t + 30 - 25 - a)(- 2t + 100)
= - 1/2t² + (15 + 2a)t + 100(5 - a).
∴对称轴为t = -(15 + 2a)/(2×(-1/2)) = 15 + 2a.
∵ - 1/2<0,
∴抛物线开口向下.
∵要使每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴15 + 2a ≥ 20,解得a ≥ 2.5.
又a<6,
∴2.5 ≤ a<6.
答:a的取值范围是2.5 ≤ a<6.
查看更多完整答案,请扫码查看


