《2025年诚成教育学业评价九年级数学全一册人教版》

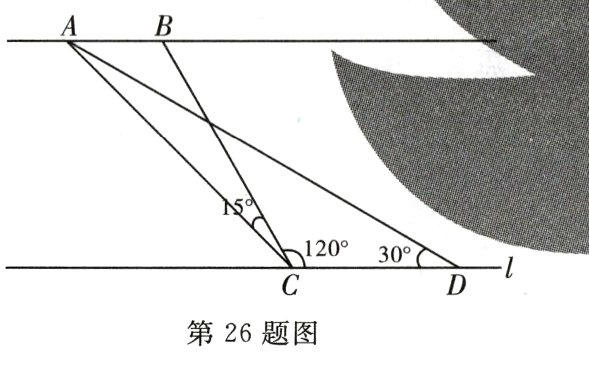
26. (8分)如图所示，九年级(1)班数学兴趣小组为了测量河对岸的古树$A$，$B$之间的距离，他们在河边与$AB$平行的直线$l$上取相距60米的$C$，$D$两点，测得$\angle ACB = 15^{\circ}$，$\angle BCD = 120^{\circ}$，$\angle ADC = 30^{\circ}$.
(1)求河的宽度；
(2)求古树$A$，$B$之间的距离.

答案：
解:
(1)如图，过点A作$AE\perp l$，垂足为E.
　　　　设$CE = x$.
　　　　　$\because CD = 60$，
　　　　　$\therefore DE = CE + CD = x + 60$.
　　　　　$\because\angle ACB = 15^{\circ}$，$\angle BCD = 120^{\circ}$，
　　　　　$\therefore\angle ACE = 180^{\circ}-\angle ACB - \angle BCD = 45^{\circ}$.
　　　　在$Rt\triangle AEC$中，
　　　　$AE = CE\cdot\tan45^{\circ}= x$.
　　　　在$Rt\triangle ADE$中，$\angle ADE = 30^{\circ}$，
　　　　$\therefore\tan30^{\circ}=\frac{AE}{ED}=\frac{x}{x + 60}=\frac{\sqrt{3}}{3}$.
　　　　$\therefore x = 30\sqrt{3}+ 30$.
　　　　$\therefore AE = (30\sqrt{3}+ 30)$米.
$\therefore$河的宽度为$(30\sqrt{3}+ 30)$米.
(2)如图，过点B作$BF\perp l$，垂足为F，
　　　　　则$CE = AE = BF = 30\sqrt{3}+ 30$，$AB = EF$.
　　　　　$\because\angle BCD = 120^{\circ}$，
　　　　　$\therefore\angle BCF = 180^{\circ}-\angle BCD = 60^{\circ}$.
　　　　　在$Rt\triangle BCF$中，
　　　　$CF = \frac{BF}{\tan60^{\circ}}=\frac{30\sqrt{3}+ 30}{\sqrt{3}} = 30 + 10\sqrt{3}$，$\therefore AB = EF = CE - CF$
　　　　　　　　　　$= 30\sqrt{3}+ 30-(30 + 10\sqrt{3})$
　　　　　　　　　　$= 20\sqrt{3}$(米).
　　　　　$\therefore$古树A，B之间的距离为$20\sqrt{3}$米.
　　　　

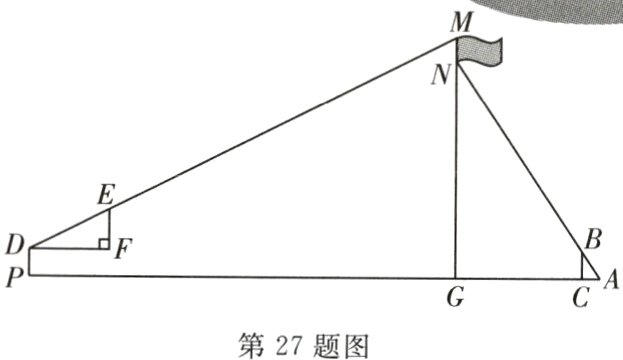
27. (10分)新理念 项目性试题 庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行，习近平总书记重要讲话引发各界青年热烈反响.某校为庆祝共青团成立100周年升起了共青团旗帜，李优和贺基旭想用所学知识测量该旗帜的宽度$MN$的长，他们进行了如下操作：如图，首先，李优在$C$处竖立一根杆标$BC$，地面上的点$A$、标杆顶端$B$和点$N$在一条直线上，测得$BC = 1.5$米，$AC = 1$米，$AG = 8$米，然后，贺基旭手持自制的直角三角形纸板$DEF$，使长直角边$DF$与水平地面平行，调整位置，恰好在点$P$时点$D$，$E$，$M$在一条直线上，$DP = 1.5$米，$PG = 23.6$米，$DF = 2EF$，已知$DP\perp PA$，$MG\perp PA$，$BC\perp PA$，点$P$，$G$，$C$，$A$在同一水平直线上，点$N$在$MG$上，求旗帜的宽度$MN$的长.

答案：
解:如图，延长DF交MG于点Q，则$DQ\perp MG$，
$DQ = PG = 23.6$，$GQ = DP = 1.5$.
　　　$\because BC\perp AP$，$MG\perp AP$，
　　　$\therefore BC// MG$.
　　　$\therefore\triangle ABC\sim\triangle ANG$.
　　　$\therefore\frac{BC}{NG}=\frac{AC}{AG}$，即$\frac{1.5}{NG}=\frac{1}{8}$.
　　　$\therefore NG = 12$.
　　　同理，得$\triangle DEF\sim\triangle DMQ$.
　　　$\therefore\frac{EF}{MQ}=\frac{DF}{DQ}$.
　　　$\because DF = 2EF$，
　　　$\therefore MQ = \frac{1}{2}DQ$
$=\frac{1}{2}\times 23.6 = 11.8$.
　　　$\therefore MN = MQ + QG - GN$
　　　　　　$= 11.8 + 1.5 - 12$
　　　　　　$= 1.3$(米).
　　　答:旗帜的宽度MN的长是1.3米.