2025年诚成教育学业评价九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年诚成教育学业评价九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第149页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
24. (6分)如图,在正方形$ABCD$中,$M$是$AD$的中点,$BE = 3AE$,试求$\angle ECM$的三个三角函数值.
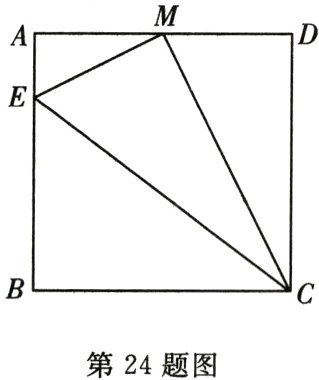

答案:
解:设$AE = x(x\gt0)$,
则$BE = 3x,BC = CD = 4x$,
$AM = MD = 2x$.
$\therefore EC=\sqrt{(3x)^2+(4x)^2}=5x$,
$EM=\sqrt{x^2+(2x)^2}=\sqrt{5}x$,
$CM=\sqrt{(2x)^2+(4x)^2}=2\sqrt{5}x$.
$\therefore EM^2 + CM^2 = CE^2$.
$\therefore\triangle CEM$是直角三角形,$\angle EMC = 90^{\circ}$.
$\therefore\sin\angle ECM=\frac{EM}{CE}=\frac{\sqrt{5}x}{5x}=\frac{\sqrt{5}}{5}$,
$\cos\angle ECM=\frac{CM}{CE}=\frac{2\sqrt{5}x}{5x}=\frac{2\sqrt{5}}{5}$,
$\tan\angle ECM=\frac{EM}{CM}=\frac{\sqrt{5}x}{2\sqrt{5}x}=\frac{1}{2}$.
则$BE = 3x,BC = CD = 4x$,
$AM = MD = 2x$.
$\therefore EC=\sqrt{(3x)^2+(4x)^2}=5x$,
$EM=\sqrt{x^2+(2x)^2}=\sqrt{5}x$,
$CM=\sqrt{(2x)^2+(4x)^2}=2\sqrt{5}x$.
$\therefore EM^2 + CM^2 = CE^2$.
$\therefore\triangle CEM$是直角三角形,$\angle EMC = 90^{\circ}$.
$\therefore\sin\angle ECM=\frac{EM}{CE}=\frac{\sqrt{5}x}{5x}=\frac{\sqrt{5}}{5}$,
$\cos\angle ECM=\frac{CM}{CE}=\frac{2\sqrt{5}x}{5x}=\frac{2\sqrt{5}}{5}$,
$\tan\angle ECM=\frac{EM}{CM}=\frac{\sqrt{5}x}{2\sqrt{5}x}=\frac{1}{2}$.
25. (8分)如图,在$Rt\triangle ABC$中,$\angle A = 90^{\circ}$,$BC$的垂直平分线交$AC$于点$D$,延长$AC$至$E$,使$CE = AB$.
(1)若$AE = 1$,求$\triangle ABD$的周长;
(2)若$AD=\frac{1}{3}BD$,求$\tan\angle ABC$的值.
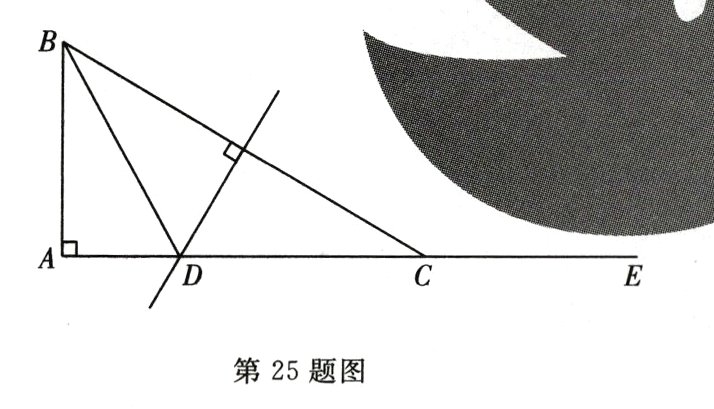
(1)若$AE = 1$,求$\triangle ABD$的周长;
(2)若$AD=\frac{1}{3}BD$,求$\tan\angle ABC$的值.

答案:
解:
(1) $\because$点$D$在线段$BC$的垂直平分线上,
$\therefore BD = CD$.
又$CE = AB$,
$\therefore\triangle ABD$的周长$=AB + AD + BD$
$=CE + AD + DC$
$=AE$
$=1$.
故$\triangle ABD$的周长为$1$.
(2) 设$AD = x(x\gt0)$.
$\because AD=\frac{1}{3}BD$,
$\therefore BD = 3x$.
又$BD = CD$,
$\therefore AC = AD + CD = 4x$.
在$Rt\triangle ABD$中,
$AB=\sqrt{BD^2 - AD^2}$
$=\sqrt{(3x)^2 - x^2}$
$=2\sqrt{2}x$.
$\therefore\tan\angle ABC=\frac{AC}{AB}=\frac{4x}{2\sqrt{2}x}=\sqrt{2}$.
(1) $\because$点$D$在线段$BC$的垂直平分线上,
$\therefore BD = CD$.
又$CE = AB$,
$\therefore\triangle ABD$的周长$=AB + AD + BD$
$=CE + AD + DC$
$=AE$
$=1$.
故$\triangle ABD$的周长为$1$.
(2) 设$AD = x(x\gt0)$.
$\because AD=\frac{1}{3}BD$,
$\therefore BD = 3x$.
又$BD = CD$,
$\therefore AC = AD + CD = 4x$.
在$Rt\triangle ABD$中,
$AB=\sqrt{BD^2 - AD^2}$
$=\sqrt{(3x)^2 - x^2}$
$=2\sqrt{2}x$.
$\therefore\tan\angle ABC=\frac{AC}{AB}=\frac{4x}{2\sqrt{2}x}=\sqrt{2}$.
26. (8分)某地修建一座以“讲袁隆平故事,厚植种子情怀”为主题的半径为800 m的圆形纪念园.如图,纪念园的中心点$A$位于$C$村西南方向和$B$村南偏东$60^{\circ}$方向上,$C$村在$B$村的正东方,且两村相距2.4 km.有关部门计划在$B$,$C$两村之间修一条笔直的公路来连接两村.问该公路是否穿过纪念园?试通过计算加以说明.(参考数据:$\sqrt{3}\approx1.73$,$\sqrt{2}\approx1.41$)
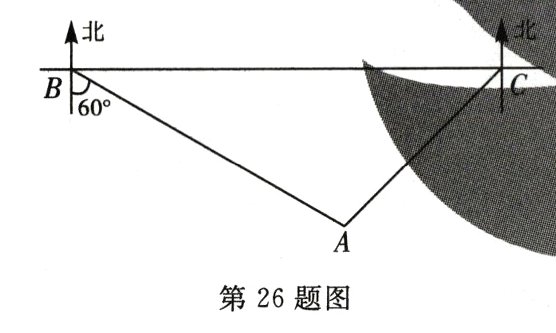

答案:
解:如图,过点$A$作$AD⊥BC$于点$D$.
由题意知,$\angle ABC = 90^{\circ}-60^{\circ}=30^{\circ}$,
$\angle ACD = 45^{\circ}$,
$\therefore BD=\sqrt{3}AD,CD = AD$.
$\because BC = 2.4\ km = 2400\ m$,
$\therefore\sqrt{3}AD + AD = 2400$.
$\therefore AD = 1200(\sqrt{3}-1)\approx876(m)$.
$\because 876\gt800$,
$\therefore$该公路没有穿过纪念园.

解:如图,过点$A$作$AD⊥BC$于点$D$.
由题意知,$\angle ABC = 90^{\circ}-60^{\circ}=30^{\circ}$,
$\angle ACD = 45^{\circ}$,
$\therefore BD=\sqrt{3}AD,CD = AD$.
$\because BC = 2.4\ km = 2400\ m$,
$\therefore\sqrt{3}AD + AD = 2400$.
$\therefore AD = 1200(\sqrt{3}-1)\approx876(m)$.
$\because 876\gt800$,
$\therefore$该公路没有穿过纪念园.

27. (10分)新理念 项目性试题 北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分别为$AB$,$BC$两部分,小明同学在点$C$处测得雪道$BC$的坡度$i = 1:2.4$,在点$A$处测得点$B$的俯角$\angle DAB = 30^{\circ}$.若雪道$AB$长为270 m,雪道$BC$长为260 m.
(1)求该滑雪场的高度$h$;
(2)据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少$35\ m^{3}$,且甲设备造雪$150\ m^{3}$所用的时间与乙设备造雪$500\ m^{3}$所用的时间相等.求甲、乙两种设备每小时的造雪量.
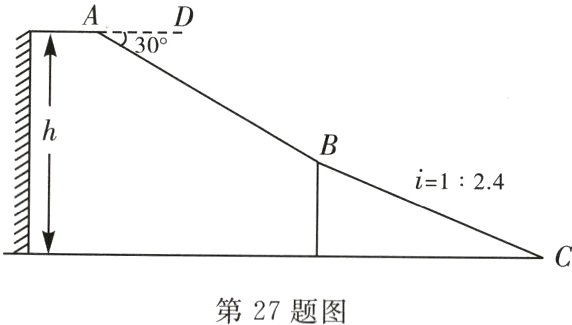
(1)求该滑雪场的高度$h$;
(2)据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少$35\ m^{3}$,且甲设备造雪$150\ m^{3}$所用的时间与乙设备造雪$500\ m^{3}$所用的时间相等.求甲、乙两种设备每小时的造雪量.

答案:
解:
(1) 如图,过点$B$作$BF// AD$,过点$A$作$AF\perp AD$,两直线交于点$F$,过点$B$作$BE$垂直地面于点$E$.
根据题意,得$\angle ABF=\angle DAB = 30^{\circ}$.
$\therefore AF=\frac{1}{2}AB = 135$.
$\because BC$的坡度$i = 1:2.4$,
$\therefore BE:CE = 1:2.4$.
设$BE = t$,则$CE = 2.4t$.
$\because BE^2 + CE^2 = BC^2$,
$\therefore t^2+(2.4t)^2 = 260^2$.
解得$t = 100$(舍去负值).
$\therefore h = AF + BE = 235(m)$.
答:该滑雪场的高度$h$为$235\ m$.

(2) 设甲种设备每小时的造雪量是$x\ m^3$,则乙种设备每小时的造雪量是$(x + 35)m^3$.
根据题意,得
$\frac{150}{x}=\frac{500}{x + 35}$.解得$x = 15$.
经检验$x = 15$是原方程的解,且符合题意.
$\therefore x + 35 = 50$.
答:甲种设备每小时的造雪量是$15\ m^3$,乙种设备每小时的造雪量是$50\ m^3$.
解:
(1) 如图,过点$B$作$BF// AD$,过点$A$作$AF\perp AD$,两直线交于点$F$,过点$B$作$BE$垂直地面于点$E$.
根据题意,得$\angle ABF=\angle DAB = 30^{\circ}$.
$\therefore AF=\frac{1}{2}AB = 135$.
$\because BC$的坡度$i = 1:2.4$,
$\therefore BE:CE = 1:2.4$.
设$BE = t$,则$CE = 2.4t$.
$\because BE^2 + CE^2 = BC^2$,
$\therefore t^2+(2.4t)^2 = 260^2$.
解得$t = 100$(舍去负值).
$\therefore h = AF + BE = 235(m)$.
答:该滑雪场的高度$h$为$235\ m$.

(2) 设甲种设备每小时的造雪量是$x\ m^3$,则乙种设备每小时的造雪量是$(x + 35)m^3$.
根据题意,得
$\frac{150}{x}=\frac{500}{x + 35}$.解得$x = 15$.
经检验$x = 15$是原方程的解,且符合题意.
$\therefore x + 35 = 50$.
答:甲种设备每小时的造雪量是$15\ m^3$,乙种设备每小时的造雪量是$50\ m^3$.
28. (10分)新理念 阅读理解试题 阅读下列材料,并完成相应的任务.
我们所学的锐角三角函数反映了直角三角形中的边角关系:
如图①,$\sin\alpha=\frac{BC}{AB}$,$\cos\alpha=\frac{AC}{AB}$,$\tan\alpha=\frac{BC}{AC}$.
一般地,当$\alpha$,$\beta$为任意角时,$\sin(\alpha+\beta)$与$\sin(\alpha - \beta)$的值可以用下面的公式求得:
$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$;$\sin(\alpha - \beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$.
例如:$\sin15^{\circ}=\sin(45^{\circ}-30^{\circ})=\sin45^{\circ}\cos30^{\circ}-\cos45^{\circ}\sin30^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}$.
任务:
(1)计算:$\sin75^{\circ}=$________;
(2)如图②,在$\triangle ABC$中,$\angle B = 15^{\circ}$,$\angle C = 45^{\circ}$,$AC = 2\sqrt{3}-2$,求$AB$和$BC$的长.
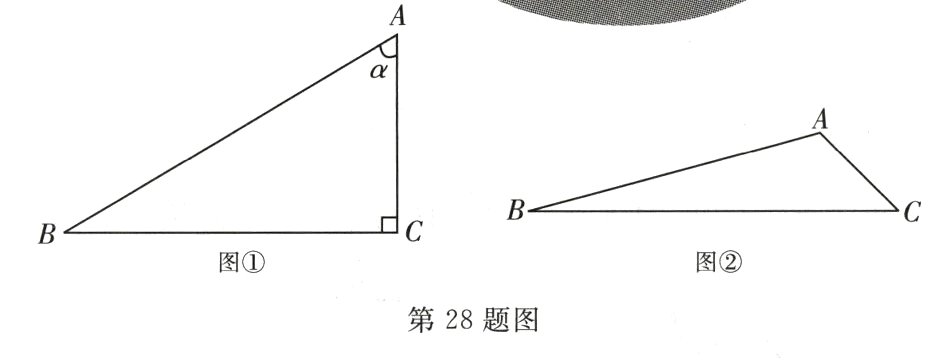
我们所学的锐角三角函数反映了直角三角形中的边角关系:
如图①,$\sin\alpha=\frac{BC}{AB}$,$\cos\alpha=\frac{AC}{AB}$,$\tan\alpha=\frac{BC}{AC}$.
一般地,当$\alpha$,$\beta$为任意角时,$\sin(\alpha+\beta)$与$\sin(\alpha - \beta)$的值可以用下面的公式求得:
$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$;$\sin(\alpha - \beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$.
例如:$\sin15^{\circ}=\sin(45^{\circ}-30^{\circ})=\sin45^{\circ}\cos30^{\circ}-\cos45^{\circ}\sin30^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}$.
任务:
(1)计算:$\sin75^{\circ}=$________;
(2)如图②,在$\triangle ABC$中,$\angle B = 15^{\circ}$,$\angle C = 45^{\circ}$,$AC = 2\sqrt{3}-2$,求$AB$和$BC$的长.

答案:
解:
(1) $\frac{\sqrt{2}+\sqrt{6}}{4}$.
(2) 如图,过点$A$作$AD⊥BC$于点$D$.
$\because\angle C = 45^{\circ}$,
$\therefore\angle DAC = 45^{\circ}$.
$\therefore AD = CD$.
$\because\sin C=\frac{AD}{AC},AC = 2\sqrt{3}-2$,
$\therefore\frac{\sqrt{2}}{2}=\frac{AD}{2\sqrt{3}-2}$.
$\therefore AD=\sqrt{6}-\sqrt{2}$.
$\therefore CD=\sqrt{6}-\sqrt{2}$.
$\because\angle B = 15^{\circ},\sin B=\frac{AD}{AB}$,
$\therefore\frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{AB}$.
$\therefore AB = 4$.
$\because\angle BAD = 90^{\circ}-\angle B = 75^{\circ}$,
$\sin\angle BAD=\frac{BD}{AB}$,
$\therefore\frac{\sqrt{2}+\sqrt{6}}{4}=\frac{BD}{4}$.
$\therefore BD=\sqrt{2}+\sqrt{6}$.
$\therefore BC = BD + CD$
$=\sqrt{2}+\sqrt{6}+\sqrt{6}-\sqrt{2}$
$=2\sqrt{6}$.

解:
(1) $\frac{\sqrt{2}+\sqrt{6}}{4}$.
(2) 如图,过点$A$作$AD⊥BC$于点$D$.
$\because\angle C = 45^{\circ}$,
$\therefore\angle DAC = 45^{\circ}$.
$\therefore AD = CD$.
$\because\sin C=\frac{AD}{AC},AC = 2\sqrt{3}-2$,
$\therefore\frac{\sqrt{2}}{2}=\frac{AD}{2\sqrt{3}-2}$.
$\therefore AD=\sqrt{6}-\sqrt{2}$.
$\therefore CD=\sqrt{6}-\sqrt{2}$.
$\because\angle B = 15^{\circ},\sin B=\frac{AD}{AB}$,
$\therefore\frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{AB}$.
$\therefore AB = 4$.
$\because\angle BAD = 90^{\circ}-\angle B = 75^{\circ}$,
$\sin\angle BAD=\frac{BD}{AB}$,
$\therefore\frac{\sqrt{2}+\sqrt{6}}{4}=\frac{BD}{4}$.
$\therefore BD=\sqrt{2}+\sqrt{6}$.
$\therefore BC = BD + CD$
$=\sqrt{2}+\sqrt{6}+\sqrt{6}-\sqrt{2}$
$=2\sqrt{6}$.

查看更多完整答案,请扫码查看


