《2025年新课标教材同步导练八年级数学下册北师大版C版》

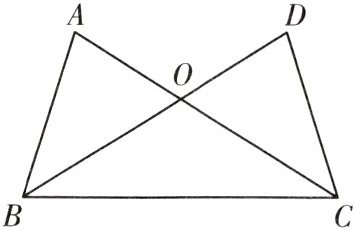
13. (2021·无锡）已知：如图，AC、DB相交于点O，AB = DC，∠ABO = ∠DCO.
求证：(1）△ABO≌△DCO；
(2）∠OBC = ∠OCB.

答案： 证明：
(1)在$\triangle ABO$和$\triangle DCO$中，
$\begin{cases}\angle AOB = \angle COD \\\angle ABO = \angle DCO \\AB = DC\end{cases}$，$\therefore \triangle ABO\cong\triangle DCO(AAS)$。
(2)由
(1)知，$\triangle ABO\cong\triangle DCO$，$\therefore OB = OC$
$\therefore \angle OBC = \angle OCB$。

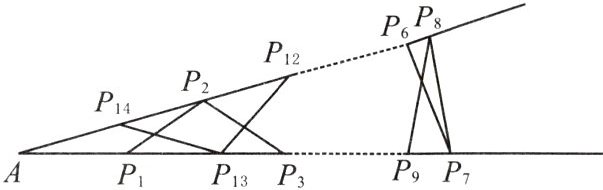
14. 如图钢架中，焊上等长的13根钢条来加固钢架，若AP₁ = P₁P₂ = P₂P₃ = … = P₁₃P₁₄ = P₁₄A，求∠A的度数.

答案： 设$\angle A = x^{\circ}$，由图形的对称性和线段长度相等及三角形的一个外角等于与它不相邻的两个内角的和可推出$\triangle AP_{7}P_{8}$中$\angle AP_{7}P_{8} = \angle AP_{8}P_{7} = 7x^{\circ}$，$\therefore x^{\circ} + 7x^{\circ} + 7x^{\circ} = 180^{\circ}$，$\therefore x = 12^{\circ}$，$\therefore \angle A = 12^{\circ}$。

15. 如图，△ABC中，AB = AC，点D在AB上，点E在AC的延长线上，且BD = CE，DE交BC于F，求证：DF = EF.

答案： 过点$D$作$DM// AC$交$BC$于$M$，
$\therefore \angle DMB = \angle ACB$，$\angle FDM = \angle E$。
$\because AB = AC$，$\therefore \angle B = \angle ACB$，
$\therefore \angle B = \angle DMB$，$\therefore BD = MD$。
$\because BD = CE$，$\therefore MD = CE$。
在$\triangle DMF$和$\triangle ECF$中，
$\begin{cases}\angle MDF = \angle E \\\angle MFD = \angle CFE \\MD = CE\end{cases}$
$\therefore \triangle DMF\cong\triangle ECF(AAS)$，$\therefore DF = EF$。

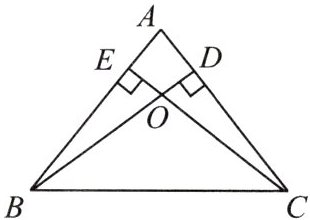
16. 如图，已知△ABC中，AB = AC，BD、CE是高，BD与CE相交于点O.
(1）求证：OB = OC；
(2）若∠ABC = 50°，求∠BOC的度数.

答案：
(1)$\because AB = AC$，$\therefore \angle ABC = \angle ACB$。
$\because BD$、$CE$是$\triangle ABC$的两条高线，
$\therefore \angle BEC = \angle BDC = 90^{\circ}$，
$\therefore \triangle BEC\cong\triangle CDB$，
$\therefore \angle DBC = \angle ECB$，$BE = CD$。
在$\triangle BOE$和$\triangle COD$中，
$\because \angle BOE = \angle COD$，$BE = CD$，
$\angle BEC = \angle BDC = 90^{\circ}$。
$\therefore \triangle BOE\cong\triangle COD$，$\therefore OB = OC$。
(2)$\because \angle ABC = 50^{\circ}$，$AB = AC$，
$\therefore \angle A = 180^{\circ} - 2\times50^{\circ} = 80^{\circ}$，
$\therefore \angle DOE + \angle A = 180^{\circ}$，
$\therefore \angle BOC = \angle DOE = 180^{\circ} - 80^{\circ} = 100^{\circ}$。