第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
11. 一组同学在校门口拍一张合影,已知冲一张底片需要0.6元,洗一张照片需要0.4元,每人都得到一张照片,每人平均分摊的钱不多于0.8元,那么参加合影的同学至少有几人? (只列关系式)
答案:
设参加合影的同学有$x$人,则$x$应满足的关系为:$0.6 + 0.4x\leq0.8x$
12. 比较下面四个算式结果的大小(在横线上选填“>”“<”“ = ”).
$4^{2}+5^{2}$______$2×4×5$;
$(-1)^{2}+2^{2}$______$2×(-1)×2$;
$(\sqrt{3})^{2}+(\frac{1}{3})^{2}$______$2×\sqrt{3}×\frac{1}{3}$;
$3^{2}+3^{2}$______$2×3×3$;
通过观察归纳,写出反映这种规律的一般结论:______________________.
$4^{2}+5^{2}$______$2×4×5$;
$(-1)^{2}+2^{2}$______$2×(-1)×2$;
$(\sqrt{3})^{2}+(\frac{1}{3})^{2}$______$2×\sqrt{3}×\frac{1}{3}$;
$3^{2}+3^{2}$______$2×3×3$;
通过观察归纳,写出反映这种规律的一般结论:______________________.
答案:
$>,>,>,=$. 一般结论为$a^{2}+b^{2}\geq2ab$.
13. (2020·自贡)我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法. 例如,代数式$|x - 2|$的几何意义是数轴上$x$所对应的点与2所对应的点之间的距离:因为$|x + 1| = |x - (-1)|$,所以$|x + 1|$的几何意义就是数轴上$x$所对应的点与 - 1所对应的点之间的距离.
(1)发现问题:代数式$|x + 1| + |x - 2|$的最小值是多少?
(2)探究问题:如图,点$A$、$B$、$P$分别表示数 - 1、2、$x$,$AB = 3$.
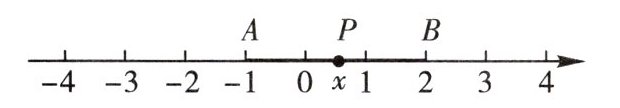
∵$|x + 1| + |x - 2|$的几何意义是线段$PA$与$PB$的长度之和,
∴当点$P$在线段$AB$上时,$PA + PB = 3$,当点$P$在点$A$的左侧或点$B$的右侧时,$PA + PB > 3$.
∴$|x + 1| + |x - 2|$的最小值是3.
(3)解决问题:
①$|x - 4| + |x + 2|$的最小值是________;
②利用上述思想方法解不等式:$|x + 3| + |x - 1| > 4$;
③当$a$为何值时,代数式$|x + a| + |x - 3|$的最小值是2.
(1)发现问题:代数式$|x + 1| + |x - 2|$的最小值是多少?
(2)探究问题:如图,点$A$、$B$、$P$分别表示数 - 1、2、$x$,$AB = 3$.
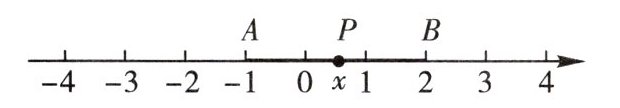
∵$|x + 1| + |x - 2|$的几何意义是线段$PA$与$PB$的长度之和,
∴当点$P$在线段$AB$上时,$PA + PB = 3$,当点$P$在点$A$的左侧或点$B$的右侧时,$PA + PB > 3$.
∴$|x + 1| + |x - 2|$的最小值是3.
(3)解决问题:
①$|x - 4| + |x + 2|$的最小值是________;
②利用上述思想方法解不等式:$|x + 3| + |x - 1| > 4$;
③当$a$为何值时,代数式$|x + a| + |x - 3|$的最小值是2.
答案:
解:
(3)① 6;
②如图所示,满足$|x + 3|+|x - 1|=|x - (-3)|+|x - 1|>4$,表示到 - 3 和 1 距离之和大于 4 的范围,当点在 - 3 和 1 之间时,距离之和为 4,不满足题意;当点在 - 3 的左边或 1 的右边时,距离之和大于 4,则$x$范围为$x < - 3$或$x>1$;
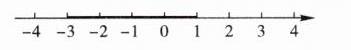
③当$a$为 - 1 或 - 5 时,代数式$|x + a|+|x - 3|$的最小值是 2.
解:
(3)① 6;
②如图所示,满足$|x + 3|+|x - 1|=|x - (-3)|+|x - 1|>4$,表示到 - 3 和 1 距离之和大于 4 的范围,当点在 - 3 和 1 之间时,距离之和为 4,不满足题意;当点在 - 3 的左边或 1 的右边时,距离之和大于 4,则$x$范围为$x < - 3$或$x>1$;
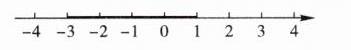
③当$a$为 - 1 或 - 5 时,代数式$|x + a|+|x - 3|$的最小值是 2.
查看更多完整答案,请扫码查看


