《2025年新课标教材同步导练八年级数学下册北师大版C版》

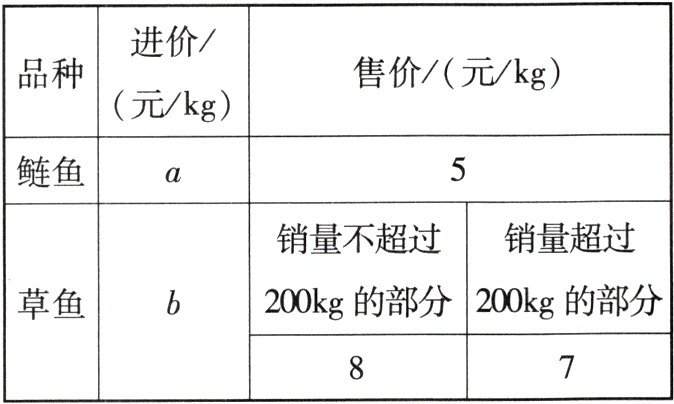
12. (2021·襄阳)为了切实保护汉江生态环境，襄阳市政府对汉江襄阳段实施全面禁渔. 禁渔后，某水库自然生态养殖的鱼在市场上热销，经销商老李每天从该水库购进草鱼和鲢鱼进行销售，两种鱼的进价和售价如表所示：
已知老李购进10kg鲢鱼和20kg草鱼需要155元，购进20kg鲢鱼和10kg草鱼需要130元.
(1)求$a,b$的值；
(2)老李每天购进两种鱼共300kg，并在当天都销售完，其中销售鲢鱼不少于80kg且不超过120kg，设每天销售鲢鱼$x$kg(销售过程中损耗不计).
①分别求出每天销售鲢鱼获利$y_{1}$(元)，销售草鱼获利$y_{2}$(元)与$x$的函数关系式，并写出$x$的取值范围；
②端午节这天，老李让利销售，将鲢鱼售价每kg降低$m$元，草鱼售价全部定为7元/kg，为了保证当天销售这两种鱼总获利$W$(元)最小值不少于320元，求$m$的最大值.

答案： 解：
(1) 根据题意，得 $\begin{cases}10a + 20b = 155\\20a + 10b = 130\end{cases}$，
解得 $\begin{cases}a = 3.5\\b = 6\end{cases}$.
(2) ①由题意，得 $y_{1}=(5 - 3.5)x = 1.5x(80\leqslant x\leqslant120)$，当 $300 - x\leqslant200$ 时，$100\leqslant x\leqslant120$，$y_{2}=(8 - 6)\times(300 - x)= - 2x + 600$；当 $300 - x ＞ 200$ 时，$80\leqslant x ＜ 100$，$y_{2}=(8 - 6)\times200+(7 - 6)\times(300 - x - 200)= - x + 500$；
$\therefore y_{2}=\begin{cases}-x + 500(80\leqslant x ＜ 100)\\-2x + 600(100\leqslant x\leqslant120)\end{cases}$；
②由题意得，$W=(5 - m - 3.5)x+(7 - 6)\times(300 - x)=(0.5 - m)x + 300$，其中 $80\leqslant x\leqslant120$，
$\because$ 当 $0.5 - m\leqslant0$ 时，$W=(0.5 - m)x + 300\leqslant300$，不合题意，$\therefore0.5 - m ＞ 0$，
$\therefore W$ 随 $x$ 的增大而增大，$\therefore$ 当 $x = 80$ 时，$W$ 的值最小，由题意得 $(0.5 - m)\times80 + 300\geqslant320$，解得 $m\leqslant0.25$，$\therefore m$ 的最大值为 $0.25$.