《2025年新课标教材同步导练八年级数学下册北师大版C版》

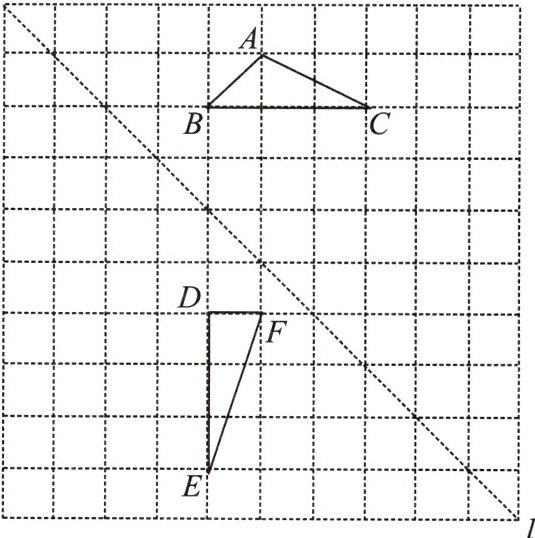
13. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC和△DEF(顶点为网格线的交点)，以及过格点的直线l.
(1)将△ABC向右平移2个单位长度，再向下平移2个单位长度，画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空：∠C + ∠E = ____________.

答案：

(1)△A'B'C'即为所求；
(2)△D'E'F'即为所求；
(3)45°.
提示：连接 A'F'，易证得△A'C'F'为等腰直角三角形，则∠A'C'F' = 45°，即∠C + ∠E = 45°.

14. 图形的操作过程(本题中四个长方形的水平方向的边长均为a，竖直方向的边长均为b)：在图A中将线段A₁A₂向右平移1个单位得到B₁B₂，得到封闭图形A₁A₂B₂B₁(即阴影部分)；在图B中将折线A₁A₂A₃向右平移1个单位得到B₁B₂B₃，得到封闭图形A₁A₂A₃B₃B₂B₁(即阴影部分).
(1)在图C中，请你类似地画一条有两个折点的折线，同样向右平移1个单位，从而得到一个封闭图形，并用斜线画出阴影.
(2)请你分别写出上述图形中除去阴影部分后剩下部分的面积：S₁ = ____ ，S₂ = ____ ，S₃ = ____.
(3)联想与探索：如图D，在一矩形草地上有一条弯曲的柏油小路(小路任何地方水平宽度都是1个单位). 请你猜想空白部分表示的草地面积是多少? 并说明你的猜想是正确的.

答案：

(1)如图 1；

(2)S₁ = ab - b，S₂ = ab - b，S₃ = ab - b；
(3)猜想草地的面积仍然是 ab - b.
方案：①将小路沿着左右两个边界“剪去”.
②将右侧的草地向左平移 1 个单位，得到一个新的长方形(图 2).
理由：在新得到的长方形中，其纵向宽度仍是 b，其水平方向的长度变成了 a - 1，所以草地的面积是 b(a - 1) = ab - b.

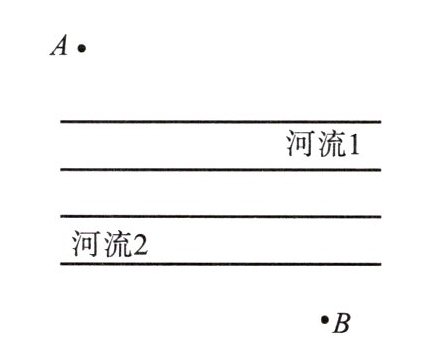
15. 如图，如果A、B两地之间有两条平行的河，现要在每一条河上造一座桥，桥造在何处才能使从A到B的路径最短? (假定河的两岸是平行的直线，桥要与河垂直)

答案：
方法 1：如图 1，将点 A 沿与第一条河流垂直的方向平移一个河宽到 A₁，将 B 沿与第二条河垂直的方向平移一个河宽到 B₁，连接 A₁B₁与两条河分别相交于 P、M，在 P、M 两处，分别建桥 PQ、MN，所得路径 AQPMNB 最短.

方法 2：如图 2，将点 A 沿与河垂直的方向平移两个河宽分别到 A₁、A₂，路径中两座桥的长度是固定的. 为了使路径最短，只要 A₂B 最短. 连接 A₂B，交河流 2 河岸于 N，在此处造桥 MN；连接 A₁M，交河流 1 河岸于 P，在此处造桥 PQ. 所得路径 AQPMNB 最短.