《2025年名校课堂九年级数学下册人教版》

1.(2024.江西)将图1所示的七巧板拼成图2所示的四边形ABCD,连接AC,则tan∠CAB=　________.

答案： $\frac{1}{2}$

2.(2024.驻马店新蔡县二模)舂（chōng）米是中国传统农业劳作方式,过程主要分为摆米、浸泡、放水、捞黄、捣击、提麸等环节,最早可追溯至数千年前的周代和春秋战国时期. 舂的结构类似于杠杆（如图1所示），一口石臼（jiù）上架着一根木头做成的“碓（duì）身”，“碓”的头部下面有杵（chǔ）. “碓”尾部的地下挖一个深坑，能使碓头翘得更高，提高舂米效率. 舂米工作时（如图2所示），碓尾落于深坑底部时，在点O处测得碓头B所在位置仰角为35°，已知坑深32cm，碓身AB长180cm，求碓头B离地面的高度.(结果精确到1cm,参考数据:sin35°≈0.57，cos35°≈0.82,tan35°≈0.70)

答案： 解:过点B作BG⊥OC于点G，过点A作AH⊥CO,交CO的延长线于点H,
∵在Rt△AHO中,AH=32cm,∠AOH=∠BOC=35°,
∴AO=$\frac{AH}{sin35°}$≈$\frac{32}{0.57}$≈56.1(cm).
∵AB=180cm，,
∴BO=AB−AO=180−56.1=123.9(cm).
∵在Rt△BOG中,∠BOG=35°,
∴BG=BO.sin35°≈123.9×0.57≈71(cm).
∴碓头B离地面的高度约为71cm.

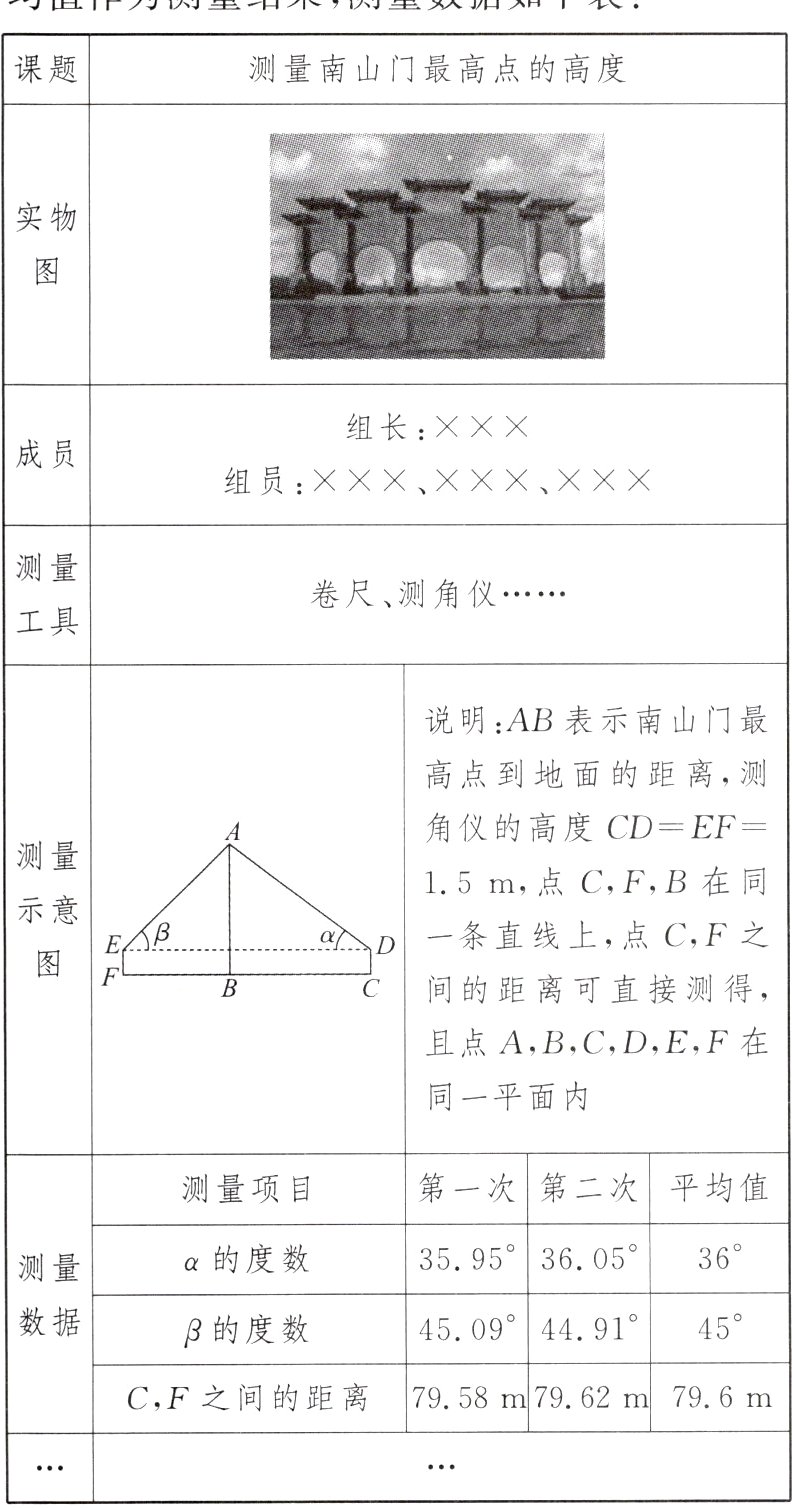
3.蔡明园公园位于河南省驻马店市上蔡县蔡都镇西南部,其公园南山门被誉为“亚洲第一门”，学完了锐角三角函数知识后，某数学“综合与实践”小组的同学把“测量南山门最高点的高度”作为一项课题活动,他们制定了测量方案，并利用课余时间完成了实地测量. 为了减小测量误差，小组在测量仰角以及两点间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表：
（1）请帮助该小组的同学根据上表中的测量数据，求南山门最高点的高度AB.(结果精确到0.1m,参考数据:sin36°≈0.59，cos36°≈0.81,tan36°≈0.73,$\sqrt{2}$≈1.41)
（2）该小组要写出一份完整的课题活动报告，除上表中的项目外，你认为还需要补充哪些项目？(写出一个即可,如需作图或作辅助线，请先将原题草图画在对应题目的答题区域后再作答)

答案： 解:
(1)设DE交AB于点G.由题意，得CD=BG=1.5m,CF =DE=79.6m,在Rt△ADG中,
∵tana=$\frac{AG}{DG}$,α=36°,..$\frac{AG}{DG}$≈0.73.在Rt△AEG中,
∵tanβ=$\frac{AG}{EG}$,β=45°,
∴$\frac{AG}{EG}$=1.
∴AG=EG.
∵DG=DE−EG=DE−AG,
∴$\frac{AG}{79.6−AG}$≈0.73.
∴AG≈33.59m.
∴AB=AG+BG=33.59+1.5≈35.1(m).答:南山门最高点的高度AB约为35.1m.
(2)还需要补充项目有:计算过程，人员分工，指导老师，活动感受等(答案不唯一，合理即可).