《2025年名校课堂九年级数学下册人教版》

1.(2023·周口项城市期末)在Rt△ABC中，∠C=90°，AB=10，AC=8，则cosB的值等于（ ）
A.$\frac{3}{5}$
B.$\frac{4}{5}$
C.$\frac{3}{4}$
D.$\frac{5}{3}$

答案： A

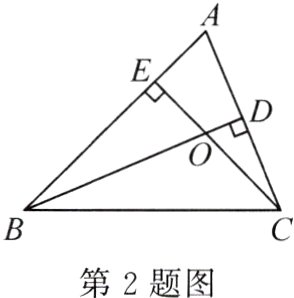
2.如图，BD⊥AC于点D，CE⊥AB于点E，BD与CE相交于点O，则图中线段的比不能表示sinA的式子为（ ）

A.$\frac{BD}{AB}$
B.$\frac{CD}{OC}$
C.$\frac{AE}{AD}$
D.$\frac{BE}{OB}$

答案： C

3.(2024·南阳模拟)如图，在边长相同的小正方形网格中，点A，B，C，D都在这些小正方形的顶点上，AB与CD相交于点P，则tan∠APD的值为_____.

答案： 2

4.(2023·周口沈丘县期末)已知在△ABC中，sinA=cosB=$\frac{\sqrt{2}}{2}$，则下列最准确的结论是( )
A.△ABC是直角三角形
B.△ABC是等腰三角形
C.△ABC是等腰直角三角形
D.△ABC是锐角三角形

答案： C

5.(2023·平顶山期末)已知α为锐角，且cos（α - 30°）=$\frac{\sqrt{3}}{2}$，则α=______.

答案： $60^{\circ}$

6.(2023·郑州管城区期末)计算：sin²60° - tan30°·cos30°+tan45°.

答案： 解：原式$=(\frac{\sqrt{3}}{2})^{2}-\frac{\sqrt{3}}{3}\times\frac{\sqrt{3}}{2}+1=\frac{5}{4}$。

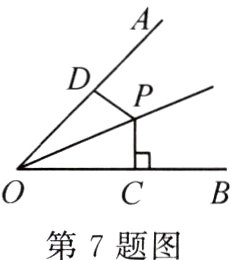
7.(2024·商丘一中模拟)如图，已知OP平分∠AOB，PC⊥OB于点C，tan∠POC=$\frac{1}{2}$，OP=$\sqrt{5}$，D为射线OA上一点，连接PD，则PD的值不可能为（ ）

A.$\frac{\sqrt{2}}{2}$
B.1
C.$\frac{\sqrt{5}}{2}$
D.2

答案： A

8.(2023·周口扶沟县期末)在△ABC中，∠ABC=105°，∠A=30°，AC=2$\sqrt{3}$+2，则AB=_____.

答案： 4

9.如图，在Rt△ABC中，∠C=90°，BC=$\sqrt{5}$，点D是AC上一点，连接BD.若tan∠A=$\frac{1}{2}$，tan∠ABD=$\frac{1}{3}$，则CD的长为_____.

答案： $\sqrt{5}$

10.如图，在△ABC中，AD是边BC上的高，E为边AC的中点，BC=14，AD=12，sinB=$\frac{4}{5}$.求：
(1)线段DC的长.
(2)tan∠EDC的值.

答案： 解：
(1) $\because AD$是边$BC$上的高，$\therefore\triangle ABD$和$\triangle ACD$都是直角三角形. 在$Rt\triangle ABD$中，$\because\sin B = \frac{4}{5},AD = 12$，$\therefore\frac{AD}{AB}=\frac{4}{5}$。$\therefore AB = 15$。$\therefore BD=\sqrt{AB^{2}-AD^{2}} = 9$。又$\because BC = 14$，$\therefore DC = BC - BD = 5$。
(2) 在$Rt\triangle ACD$中，$\because E$为斜边$AC$的中点，$\therefore ED=\frac{1}{2}AC = EC$。$\therefore\angle C=\angle EDC$。$\therefore\tan\angle EDC=\tan C=\frac{AD}{DC}=\frac{12}{5}$。