《2025年名校课堂九年级数学下册人教版》

1. 在△ABC中，∠C = 90°，AC = 3，AB = 4，欲求∠A的度数，最适宜的做法是 （ ）
A. 根据tanA的值求出∠A
B. 根据sinA的值求出∠A
C. 根据cosA的值求出∠A
D. 先根据sinB求出∠B，再利用90° - ∠B求出∠A

答案： C

2. 在Rt△ABC中，∠C = 90°，BC = $\sqrt{5}$，AB = 2$\sqrt{5}$，则∠A的度数为 （ ）
A. 90°
B. 60°
C. 45°
D. 30°

答案： D

3. 在Rt△ABC中，∠C = 90°，a，b，c分别是∠A，∠B，∠C的对边，b = 20，c = 20$\sqrt{2}$，则∠A = ______，a = ______．

答案： 45° 20

4.（教材P73例1变式）如图，在Rt△ABC中，∠C = 90°．已知BC = 2$\sqrt{6}$，AC = 6$\sqrt{2}$，解这个直角三角形．

答案： 解:
∵tanA=$\frac{BC}{AC}$=$\frac{2\sqrt{6}}{6\sqrt{2}}$=$\frac{\sqrt{3}}{3}$,
∴∠A=30°.
∴∠B=90°−∠A=90°−30°=60°,AB=2BC=4$\sqrt{6}$

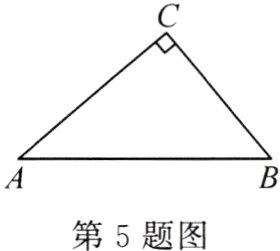
5. 如图，在△ABC中，∠C = 90°，∠B = 50°，AB = 10，则BC的长为 （ ）


A. 10tan50°
B. 10cos50°
C. 10sin50°
D. $\frac{10}{\cos50^{\circ}}$

答案： B

6. 如图，在Rt△ACB中，∠C = 90°，D是AC的中点，BC = 4，tan∠CAB = $\frac{1}{2}$，则AD的长为（ ）


A. 1
B. 2
C. 4
D. 8

答案： C

7. 在Rt△ABC中，∠C = 90°，a，b，c分别是∠A，∠B，∠C的对边的长，c = 8$\sqrt{3}$，∠A = 60°，解这个直角三角形．

答案： 解:
∵∠A=60°,∠C=90°,
∴∠B=90°−∠A=30°.
∵sinA =$\frac{a}{c}$,cosA=$\frac{b}{c}$
∴a=c·sinA=8$\sqrt{3}$×sin60°=8$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=12,b=c·cosA=8$\sqrt{3}$×$\frac{1}{2}$=4$\sqrt{3}$

8.（教材P73例2变式）如图，在Rt△ABC中，∠C = 90°，∠B = 55°，AC = 4，解这个直角三角形．（结果保留小数点后一位）

答案： 解:
∵∠B=55°,∠C=90°,
∴∠A=90°−∠B=90°−55°=35°.
∵tanB=$\frac{AC}{BC}$,sinB=$\frac{AC}{AB}$,
∴BC=$\frac{AC}{tanB}$=$\frac{4}{tan55°}$≈2.8,AB=$\frac{AC}{sinB}$=$\frac{4}{sin55°}$≈4.9.

9.（2024·洛阳汝阳县一模）在△ABC中，AB = AC，若BD⊥AC于点D，cos∠BAD = $\frac{2}{3}$，BD = $\sqrt{5}$，则CD为________．

答案： 1或5