第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 已知四边形 $ABCD$ 的对角线互相平分,要使它成为菱形,还需要添加一个条件,这个条件是( )
A.$AB = CD$
B.$AB = BC$
C.$AD = BC$
D.$AC = BD$
A.$AB = CD$
B.$AB = BC$
C.$AD = BC$
D.$AC = BD$
答案:
B 【解析】
∵ 四边形 ABCD 的对角线互相平分,
∴ 四边形 ABCD 是平行四边形. 又
∵ AB=BC(一组邻边相等),
∴ 四边形 ABCD 是菱形. 故选 B.
∵ 四边形 ABCD 的对角线互相平分,
∴ 四边形 ABCD 是平行四边形. 又
∵ AB=BC(一组邻边相等),
∴ 四边形 ABCD 是菱形. 故选 B.
2 如图,在菱形 $ABCD$ 中,对角线 $AC$,$BD$ 相交于点 $O$,下列结论中错误的是( )
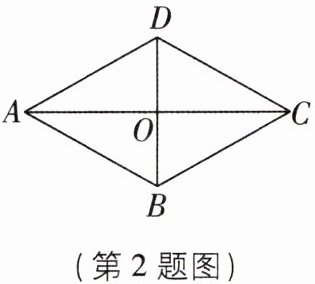
A.$AB = AD$
B.$AC\perp BD$
C.$AC = BD$
D.$\angle DAC = \angle BAC$

A.$AB = AD$
B.$AC\perp BD$
C.$AC = BD$
D.$\angle DAC = \angle BAC$
答案:
C 【解析】
∵ 四边形 ABCD 是菱形,
∴ ∠BAC=∠DAC,AB=AD,AC⊥BD,故 A,B,D 正确,无法得出 AC=BD,故选 C.
∵ 四边形 ABCD 是菱形,
∴ ∠BAC=∠DAC,AB=AD,AC⊥BD,故 A,B,D 正确,无法得出 AC=BD,故选 C.
3 [2025 四川雅安校级质检]如图,在菱形 $ABCD$ 中,对角线 $AC$,$BD$ 相交于点 $O$,点 $E$ 为 $CD$ 的中点. 若 $OE = 3$,则菱形 $ABCD$ 的周长为( )
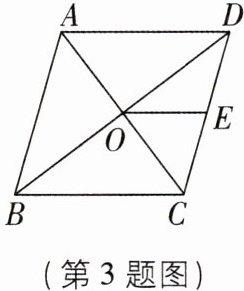
A.6
B.12
C.24
D.48

A.6
B.12
C.24
D.48
答案:
C 【解析】
∵ 四边形 ABCD 为菱形,
∴ OB=OD,AB=BC=CD=DA.
∵ 点 E 为 CD 的中点,
∴ OE 是△BCD 的中位线,
∴ BC=2OE.
∵ OE=3,
∴ BC=2OE=6,
∴ C菱形ABCD=4BC=4×6=24. 故选 C.
∵ 四边形 ABCD 为菱形,
∴ OB=OD,AB=BC=CD=DA.
∵ 点 E 为 CD 的中点,
∴ OE 是△BCD 的中位线,
∴ BC=2OE.
∵ OE=3,
∴ BC=2OE=6,
∴ C菱形ABCD=4BC=4×6=24. 故选 C.
4 [2024 甘肃兰州城关区期中]如图,在菱形 $ABCD$ 中,点 $A$ 在 $x$ 轴上,点 $B$ 的坐标为 $(8,2)$,点 $D$ 的坐标为 $(0,2)$,则点 $C$ 的坐标为( )
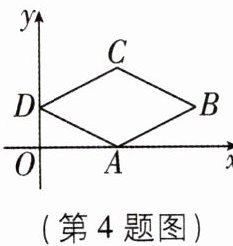
A.$(2,2)$
B.$(2,4)$
C.$(4,2)$
D.$(4,4)$

A.$(2,2)$
B.$(2,4)$
C.$(4,2)$
D.$(4,4)$
答案:
D 【解析】连接 AC,BD 交于点 E,如图所示.
∵ 四边形 ABCD 是菱形,
∴ AC⊥BD,AE=CE=$\frac{1}{2}$AC,BE=DE=$\frac{1}{2}$BD.
∵ 点 B 的坐标为(8,2),点 D 的坐标为(0,2),
∴ AE=2=OD,DE=OA=4,
∴ AC=4,
∴ 点 C 的坐标为(4,4). 故选 D.

D 【解析】连接 AC,BD 交于点 E,如图所示.
∵ 四边形 ABCD 是菱形,
∴ AC⊥BD,AE=CE=$\frac{1}{2}$AC,BE=DE=$\frac{1}{2}$BD.
∵ 点 B 的坐标为(8,2),点 D 的坐标为(0,2),
∴ AE=2=OD,DE=OA=4,
∴ AC=4,
∴ 点 C 的坐标为(4,4). 故选 D.

5 如图,在菱形 $ABCD$ 中,$AB = 1$,$\angle DAB = 60^{\circ}$,则 $AC$ 的长为( )

A.$\frac{1}{2}$
B.1
C.$\frac{\sqrt{3}}{2}$
D.$\sqrt{3}$
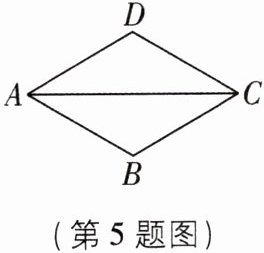
A.$\frac{1}{2}$
B.1
C.$\frac{\sqrt{3}}{2}$
D.$\sqrt{3}$

答案:
D 【解析】如图,连接 BD 交 AC 于点 O.
∵ 四边形 ABCD 是菱形,∠DAB=60°,
∴ OA=OC,∠BAO=$\frac{1}{2}$∠DAB=30°,AC⊥BD,
∴ ∠AOB=90°,
∴ OB=$\frac{1}{2}$AB=$\frac{1}{2}$,
∴ OA=$\sqrt{AB² - OB²}$=$\sqrt{1² - (\frac{1}{2})²}$=$\frac{\sqrt{3}}{2}$,
∴ AC=2OA=$\sqrt{3}$,故选 D.

D 【解析】如图,连接 BD 交 AC 于点 O.
∵ 四边形 ABCD 是菱形,∠DAB=60°,
∴ OA=OC,∠BAO=$\frac{1}{2}$∠DAB=30°,AC⊥BD,
∴ ∠AOB=90°,
∴ OB=$\frac{1}{2}$AB=$\frac{1}{2}$,
∴ OA=$\sqrt{AB² - OB²}$=$\sqrt{1² - (\frac{1}{2})²}$=$\frac{\sqrt{3}}{2}$,
∴ AC=2OA=$\sqrt{3}$,故选 D.

6 [2025 陕西榆林调研]如图,点 $E$ 是菱形 $ABCD$ 的对角线 $BD$ 上一点,连接 $AE$,若 $AD = DE$,$\angle AEB = 105^{\circ}$,则 $\angle BAE$ 的度数为______$^{\circ}$.
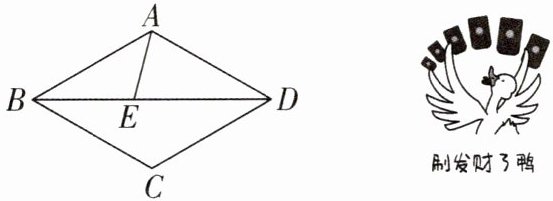

答案:
45 【解析】
∵ ∠AEB=105°,
∴ ∠AED=75°.
∵ AD=DE,
∴ ∠AED=∠EAD=75°,
∴ ∠ADB=30°.
∵ 四边形 ABCD 是菱形,
∴ AB=AD,
∴ ∠ABD=∠ADB=30°,
∴ ∠BAE=∠AED - ∠ABD=45°. 故答案为 45.
∵ ∠AEB=105°,
∴ ∠AED=75°.
∵ AD=DE,
∴ ∠AED=∠EAD=75°,
∴ ∠ADB=30°.
∵ 四边形 ABCD 是菱形,
∴ AB=AD,
∴ ∠ABD=∠ADB=30°,
∴ ∠BAE=∠AED - ∠ABD=45°. 故答案为 45.
7 [2024 河南周口调研]如图,小陶家有一个菱形中国结装饰,测得 $BD = 12\mathrm{cm}$,$AC = 16\mathrm{cm}$,$AC$,$BD$ 交于点 $O$,$EF\perp AB$ 分别交 $AB$,$CD$ 于点 $E$,$F$,则 $EF$ 的长为______$\mathrm{cm}$.
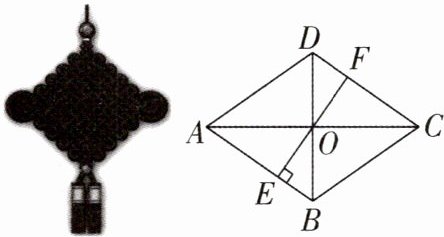

答案:
$\frac{48}{5}$ 【解析】
∵ 四边形 ABCD 是菱形,
∴ AC⊥BD,AO=$\frac{1}{2}$AC=8 cm,BO=$\frac{1}{2}$BD=6 cm,
∴ AB=$\sqrt{AO² + BO²}$=10 cm.
∵ S菱形ABCD=$\frac{1}{2}$AC·BD=AB·EF,
∴ $\frac{1}{2}$×16×12=10EF,
∴ EF=$\frac{48}{5}$ cm,故答案为 $\frac{48}{5}$.
∵ 四边形 ABCD 是菱形,
∴ AC⊥BD,AO=$\frac{1}{2}$AC=8 cm,BO=$\frac{1}{2}$BD=6 cm,
∴ AB=$\sqrt{AO² + BO²}$=10 cm.
∵ S菱形ABCD=$\frac{1}{2}$AC·BD=AB·EF,
∴ $\frac{1}{2}$×16×12=10EF,
∴ EF=$\frac{48}{5}$ cm,故答案为 $\frac{48}{5}$.
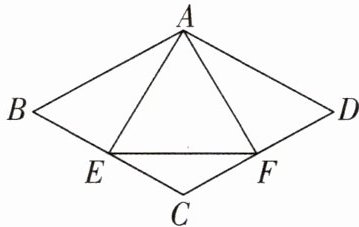
8 [2025 湖南张家界质检]如图,在菱形 $ABCD$ 中,$AE\perp BC$ 于点 $E$,$AF\perp CD$ 于点 $F$,连接 $EF$.
(1)求证:$AE = AF$;
(2)若 $\angle B = 60^{\circ}$,求 $\angle AEF$ 的度数.
(1)求证:$AE = AF$;
(2)若 $\angle B = 60^{\circ}$,求 $\angle AEF$ 的度数.

答案:
(1)【证明】
∵ 四边形 ABCD 是菱形,
∴ AB=AD,∠B=∠D. 又
∵ AE⊥BC 于点 E,AF⊥CD 于点 F,
∴ ∠AEB=∠AFD=90°. 在△ABE 与△ADF 中,{∠B=∠D,∠AEB=∠AFD,AB=AD},
∴ △ABE≌△ADF(AAS),
∴ AE=AF.
(2)【解】
∵ 四边形 ABCD 是菱形,
∴ AD//BC,
∴ ∠B+∠BAD=180°.
∵ ∠B=60°,
∴ ∠BAD=120°. 又
∵ ∠AEB=90°,∠B=60°,
∴ ∠BAE=30°. 由
(1)知△ABE≌△ADF,
∴ ∠BAE=∠DAF=30°,
∴ ∠EAF=120° - 30° - 30°=60°.
∵ 由
(1)知 AE=AF,
∴ △AEF 是等边三角形,
∴ ∠AEF=60°.
(1)【证明】
∵ 四边形 ABCD 是菱形,
∴ AB=AD,∠B=∠D. 又
∵ AE⊥BC 于点 E,AF⊥CD 于点 F,
∴ ∠AEB=∠AFD=90°. 在△ABE 与△ADF 中,{∠B=∠D,∠AEB=∠AFD,AB=AD},
∴ △ABE≌△ADF(AAS),
∴ AE=AF.
(2)【解】
∵ 四边形 ABCD 是菱形,
∴ AD//BC,
∴ ∠B+∠BAD=180°.
∵ ∠B=60°,
∴ ∠BAD=120°. 又
∵ ∠AEB=90°,∠B=60°,
∴ ∠BAE=30°. 由
(1)知△ABE≌△ADF,
∴ ∠BAE=∠DAF=30°,
∴ ∠EAF=120° - 30° - 30°=60°.
∵ 由
(1)知 AE=AF,
∴ △AEF 是等边三角形,
∴ ∠AEF=60°.
查看更多完整答案,请扫码查看


