第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1 [2025福建泉州期中]在$\triangle ABC$中,若$∠ABC= 90^{\circ }$,则下列正确的是( )
A.$BC= AB+AC$
B.$BC^{2}= AB^{2}+AC^{2}$
C.$AB^{2}= AC^{2}+BC^{2}$
D.$AC^{2}= AB^{2}+BC^{2}$
A.$BC= AB+AC$
B.$BC^{2}= AB^{2}+AC^{2}$
C.$AB^{2}= AC^{2}+BC^{2}$
D.$AC^{2}= AB^{2}+BC^{2}$
答案:
D [解析]因为在△ABC中,∠ABC=90°,所以AC²=AB²+BC².故选D.
2 [2025河南安阳质检]如图,直线$AB⊥CD$,垂足为O,$AO= 15,CO= 8$,以点A为圆心,AC的长为半径画弧,交直线AB于点E,则OE的长为( )
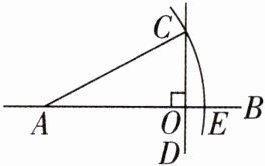
A.8
B.6
C.4
D.2

A.8
B.6
C.4
D.2
答案:
D [解析]因为AB⊥CD,所以∠COA=90°,所以AC²=AO²+OC².因为AO=15,CO=8,所以AC=17.因为以点A为圆心,AC的长为半径画弧,交直线AB于点E,所以AC=AE=17,所以OE=AE−AO=2,故选D.
3 [2025江苏泰州期中]如图,$Rt\triangle ABC$的顶点A,B都在由边长为1的小正方形组成的方格纸的格点上,且$∠C= 90^{\circ }$,则AB的长为____.
答案:
5 [解析]因为AB²=3²+4²=25,所以AB=5.故答案为5.
4 [2025广东深圳调研]如图,在$\triangle ABC$中,$CD⊥AB$于点D,E在AD上,连接CE,$AE= CE$.若$AD= 6,BC= 5,BD= 3$,则DE的长为____.
答案:
$\frac{5}{3}$ [解析]因为CD⊥AB,BD=3,BC=5,所以CD²=BC²−BD²=5²−3²=16.设AE=CE=x,则DE=6−x,所以在Rt△CDE中,CE²=DE²+CD²,即x²=(6−x)²+16,解得x=$\frac{13}{3}$,所以DE=6−$\frac{13}{3}$=$\frac{5}{3}$.故答案为$\frac{5}{3}$.
5 [2024浙江台州调研]如图,AD是$\triangle ABC$的高,分别以AB,BD,DC,CA为边向外作正方形,其中3个正方形的面积如图所示,则第四个正方形的面积为( )
A.1
B.2
C.3
D.4
A.1
B.2
C.3
D.4
答案:
C [解析]因为AD是△ABC的高,所以AD⊥BC,所以∠ADB=∠ADC=90°,所以AD²=AB²−BD²=15−6=9,所以CD²=AC²−AD²=12−9=3,所以第四个正方形的面积为3,故选C.
6 如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ },\triangle ABC的面积为24cm^{2}$,在AB同侧分别以AB,BC,AC为直径作三个半圆,则阴影部分的面积为____$cm^{2}$.
答案:
24 [解析]由勾股定理,得AB²=BC²+AC²,则阴影部分的面积为$\frac{1}{2}$π×($\frac{BC}{2}$)²+$\frac{1}{2}$π×($\frac{AC}{2}$)²+S△ABC−$\frac{1}{2}$π×($\frac{AB}{2}$)²=$\frac{1}{8}$π×(BC²+AC²−AB²)+24=24cm².
7 [2024北京海淀区期中]如图,在$\triangle ABC$中,$AB= AC= 5,BC= 6$,则AC边上的高BD的长为( )
A.4
B.4.4
C.4.8
D.5
A.4
B.4.4
C.4.8
D.5
答案:
C [解析]如图,过A作AE⊥BC于点E.
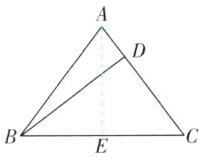
因为AB=AC,AE⊥BC,所以EB=EC=$\frac{1}{2}$CB=3.在Rt△ABE中,AE²=AB²−BE²=5²−3²=16,所以AE=4,所以△ABC的面积为$\frac{1}{2}$·BC·AE=$\frac{1}{2}$×6×4=12,所以$\frac{1}{2}$·AC·BD=12,即$\frac{1}{2}$×5×BD=12,解得BD=4.8.故选C.
C [解析]如图,过A作AE⊥BC于点E.

因为AB=AC,AE⊥BC,所以EB=EC=$\frac{1}{2}$CB=3.在Rt△ABE中,AE²=AB²−BE²=5²−3²=16,所以AE=4,所以△ABC的面积为$\frac{1}{2}$·BC·AE=$\frac{1}{2}$×6×4=12,所以$\frac{1}{2}$·AC·BD=12,即$\frac{1}{2}$×5×BD=12,解得BD=4.8.故选C.
8 [2025山东青岛期末]如图,在四边形ABCD中,$∠ABC= ∠CDA= 90^{\circ }$,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为$S_{1},S_{2},S_{3},S_{4}$,若$S_{1}= 8,S_{2}= 11,S_{3}= 15$,则$S_{4}= $____.
答案:
18 [解析]如图,连接AC.因为S₁=8,S₂=11,S₃=15,所以AD²=8,AB²=11,BC²=15.
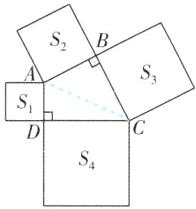
在Rt△ABC与Rt△ADC中,由勾股定理得AC²=AB²+BC²=26,CD²=AC²−AD²,所以CD²=26−8=18,所以S₄=18.故答案为18.
18 [解析]如图,连接AC.因为S₁=8,S₂=11,S₃=15,所以AD²=8,AB²=11,BC²=15.

在Rt△ABC与Rt△ADC中,由勾股定理得AC²=AB²+BC²=26,CD²=AC²−AD²,所以CD²=26−8=18,所以S₄=18.故答案为18.
9 已知一个直角三角形的两条边长分别为3和5,则第三条边长的平方为____.
答案:
16或34 [解析]因为一个直角三角形的两条边长分别为3和5,所以①当5是此直角三角形的斜边长时,设另一条直角边长为x,则由勾股定理,得x²=5²−3²=16;②当5是此直角三角形的直角边长时,设斜边长为y,则由勾股定理,得y²=5²+3²=34.故答案为16或34.
查看更多完整答案,请扫码查看


