第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 写出一个比$\sqrt{7}$小的无理数
$\sqrt{3}$(答案不唯一)
。
答案:
1 $\sqrt{3}$(答案不唯一)
2. 要使$\sqrt{x + 1}$有意义,$x$的值可以是
2
(写出一个即可)。
答案:
2 1(答案不唯一)
3. 在$\triangle ABC$中,$AB = 3$,$AC = 4$,则$BC$的长度可能是
3
(写出一个符合要求的值即可)。
答案:
3 2(满足$1<BC<7$的任意实数,答案不唯一)
4. 已知一次函数$y = x + b$($b$为常数)的图象不经过第二象限。写出一个符合条件的$b$的值为
0
。
答案:
4 0(答案满足$b\leq0$均可)
5. 如图是反比例函数$y = \frac{k}{x}(x > 0)$的图象,写出一个符合要求的整数$k$的值是
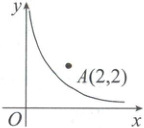
1(或2或3,答案不唯一)
。
答案:
5 1(或2或3,答案不唯一)
6. 某食品零售店计划购进100千克软糖,第一次购进A软糖$m$千克,进价为每千克12元;第二次购进B软糖$(100 - m)$千克,进价为每千克18元。现将两种软糖混合后以每千克15元出售,若商店售完这些软糖能够盈利,且正整数$m$是10的倍数,则$m$的值可以是
60
(只要写出一个满足条件的$m$即可)。
答案:
6 60(答案不唯一,60,70,80,90均可)
7. 问题:如图,在平行四边形$ABCD$中,点$E$,$F$在对角线$AC$上(不与点$A$,$C$重合),连接$DE$,$DF$,$BE$,$BF$。若______,求证:四边形$DEBF$是平行四边形。
请在①$AE = CF$,②$\angle ADE = \angle CBF$,③$DE = BF$中只选择一个作为条件,把序号补充在问题横线上,并完成问题的解答。
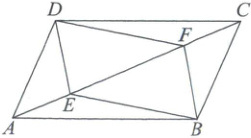
请在①$AE = CF$,②$\angle ADE = \angle CBF$,③$DE = BF$中只选择一个作为条件,把序号补充在问题横线上,并完成问题的解答。

答案:
7 平行四边形的判定与性质
证明:选择①,连接$DB$交$AC$于点$O$,如图所示.
$\because$四边形$ABCD$为平行四边形,
$\therefore BO = DO,AO = CO$.
$\because AE = CF$,
$\therefore AO - AE = CO - CF$.
$\therefore EO = FO$.
$\therefore$四边形$DEBF$为平行四边形.

选择②,连接$DB$交$AC$于点$O$,如图所示.
$\because$四边形$ABCD$为平行四边形,
$\therefore BO = DO,AO = CO,AD// BC,AD = BC$.
$\therefore \angle DAE = \angle BCF$.
$\because \angle ADE = \angle CBF$,
$\therefore \triangle ADE\cong \triangle CBF(ASA)$.
$\therefore AE = CF$.
$\therefore AO - AE = CO - CF$.
$\therefore EO = FO$.
$\therefore$四边形$DEBF$为平行四边形.
③当$DE = BF$时,不能判定四边形$DEBF$为平行四边形.
7 平行四边形的判定与性质
证明:选择①,连接$DB$交$AC$于点$O$,如图所示.
$\because$四边形$ABCD$为平行四边形,
$\therefore BO = DO,AO = CO$.
$\because AE = CF$,
$\therefore AO - AE = CO - CF$.
$\therefore EO = FO$.
$\therefore$四边形$DEBF$为平行四边形.

选择②,连接$DB$交$AC$于点$O$,如图所示.
$\because$四边形$ABCD$为平行四边形,
$\therefore BO = DO,AO = CO,AD// BC,AD = BC$.
$\therefore \angle DAE = \angle BCF$.
$\because \angle ADE = \angle CBF$,
$\therefore \triangle ADE\cong \triangle CBF(ASA)$.
$\therefore AE = CF$.
$\therefore AO - AE = CO - CF$.
$\therefore EO = FO$.
$\therefore$四边形$DEBF$为平行四边形.
③当$DE = BF$时,不能判定四边形$DEBF$为平行四边形.
1. 蜜蜂构建的蜂巢展现出了正六边形的精巧设计。如图是某校生物实验小组学生利用长度相同的小棒搭建的蜂巢结构平面图,第①个图案用了11根小棒,第②个图案用了19根小棒,第③个图案用了27根小棒,第④个图案用了35根小棒……按此规律排列下去,第⑧个图案用的小棒根数是(
$
A.59
B.67
C.75
D.96
B
)$
A.59
B.67
C.75
D.96
答案:
1 B
2. 如图,在平面直角坐标系中,边长为2的等边三角形$AOP$在第二象限,$OA$与$x$轴重合,将$\triangle AOP$绕点$O$顺时针旋转$60^{\circ}$,得到$\triangle A_1OP_1$,再作$\triangle A_1OP_1$关于原点$O$的中心对称图形,得到$\triangle A_2OP_2$,再将$\triangle A_2OP_2$绕点$O$顺时针旋转$60^{\circ}$,得到$\triangle A_3OP_3$,再作$\triangle A_3OP_3$关于原点$O$的中心对称图形,得到$\triangle A_4OP_4$……以此类推,则点$P_{2025}$的坐标是(
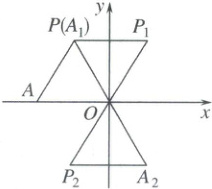
A.$(1,\sqrt{3})$
B.$(-1,-\sqrt{3})$
C.$(2,0)$
D.$(-2,0)$
D
)
A.$(1,\sqrt{3})$
B.$(-1,-\sqrt{3})$
C.$(2,0)$
D.$(-2,0)$
答案:
2 D
3. (2025·河南)观察$2x$,$4x^2$,$6x^3$,$8x^4$,…,根据这些式子的变化规律,可得第$n$个式子为
$2nx^n$
。
答案:
3 $2nx^n$
4. 如图,已知直线$a$:$y = x$,直线$b$:$y = -\frac{1}{2}x$和点$P(1,0)$,过点$P$作$y$轴的平行线交直线$a$于点$P_1$,过点$P_1$作$x$轴的平行线交直线$b$于点$P_2$,过点$P_2$作$y$轴的平行线交直线$a$于点$P_3$,过点$P_3$作$x$轴的平行线交直线$b$于点$P_4$……按此作法进行下去,则点$P_{2026}$的横坐标为
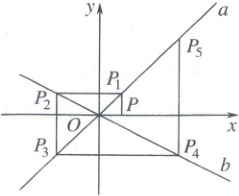
$-2^{1013}$
。
答案:
4 $-2^{1013}$
查看更多完整答案,请扫码查看


