《2026年天利38套中考试题精选数学浙江专版》

20. （本小题满分8分）函数$y=\frac{k}{x}$（$k$为常数）的图象过点$A(4,2)$，$B(1,m)$.
（1）求$k$，$m$的值.
（2）小明说：“该函数图象上的任意一点$(a,b)$，若$a ＜ 4$，则$b ＞ 2$”，你赞同小明的说法吗？请说明理由.

答案： 20. 反比例函数的图象与性质
解:
(1)
∵函数y = $\frac{k}{x}$(k为常数)的图象过点A(4, 2)，B(1, m)，
∴k = 1·m = 4×2(关键:反比例函数图象上的点(x, y)的横、纵坐标的积是定值k，即xy = k).
∴k = 8，m = 8.
(2)不赞同.理由1:当a ＜ 0时，则有b ＜ 0.理由2:当a = - 2时，则有b = - 4 ＜ 2.(取特殊值推翻结论可得分)理由3:必须强调“在同一个象限内”.

21. （本小题满分8分）某公司开发了一款App，为了解用户对该款App的满意度，随机抽取部分使用过这款App的用户进行调查.满意度分为5个等级，分别为：1星，2星，3星，4星，5星.现将收集到的数据整理后描述如下：

请根据上述信息回答问题：
（1）抽取的用户有多少人？
（2）$m =$45.
（3）满意度低于3星表示用户不满意.

据

后

台统计，有10000人使用过这款App，请估计这些用户中不满意的人数.

答案： 21. 扇形统计图+频数分布表+用样本估计总体
解:
(1)99÷(25% + 30%) = 180(人).
答:本次调查所抽取的用户人数为180.
(2)45.
[解题过程]m = 180 - 36 - 99 = 45.
(3)45÷180×100% = 25%.根据样本估计总体得，10000×25% = 2500(人).
答:这些用户中不满意的人数约为2500.

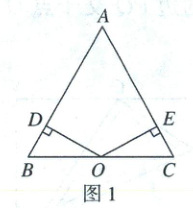
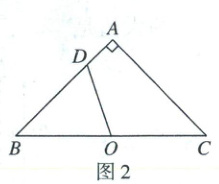
22. （本小题满分10分）如图，在$\triangle ABC$中，$AB = AC$，$O$为$BC$的中点，点$D$在边$AB$上，连接$OD$.
（1）如图1，若$OD\perp AB$，$OE\perp AC$于点$E$，求证：$OE = OD$.
（2）如图2，已知$\angle BAC = 90^{\circ}$，$AB = 4$，$AD = 1$.若点$F$在边$AC$上，$OF = OD$，求$AF$的长.

答案：
22. 全等三角形的判定与性质+等腰三角形的性质+直角三角形的性质
解:
(1)证明:如图1，连接OA.
　　　　　　　　　
∵AB = AC，O为BC的中点，
∴AO平分∠BAC(总结:等腰三角形底边的中线、高线、顶角的角平分线均重合，简称“三线合一”).
∵OD⊥AB，OE⊥AC，
∴OE = OD(方法:角平分线上的点到角两边的距离相等)(另解:证明△BOD≌△COE也可).
(2)如图2，在AC上取点F₁，使AF₁ = AD = 1，此时F点位于点F₁处，
　　　　　　　
则有OF₁ = OD，
∴AF = AF₁ = 1.作OH⊥AC于点H，在AC上取点F₂，使其与点F₁关于OH对称，此时F点位于点F₂处，则有AH = $\frac{1}{2}$AB = 2，OF₁ = OF₂ = OD，
∴HF₂ = HF₁ = 1，则AF = AF₂ = 3.
∴AF = 1或AF = 3.
(另解:连接AO，由OF = OD，得出△AOD≌△AOF或△AOD≌△COF，分别得到AF = 1或CF = 1，即AF = 1或AF = 3)
难点突破
构造全等三角形的常用方法
(1)翻折法:通过将一个三角形翻折，构造两个三角形全等，则对应边和对应角均相等；
(2)构造法:利用已知的边和角，通过几何作图构造全等三角形；
(3)中垂线法:利用中垂线定理，将一条线段分为两段，形成两个全等三角形；
(4)角平分线法:在角平分线两边构造全等三角形，确保对应角相等；
(5)辅助线法:通过延长或旋转线段，构造全等三角形.