第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
3. 阅读并完成下列问题:任意给定一个矩形 A,是否存在另一矩形 B,使它的周长和面积分别是已知矩形周长和面积的一半?
当已知矩形 A 的相邻两边长分别为 6 和 1 时,小亮同学是这样研究的:
设所求矩形的相邻两边长分别是 $x$ 和 $y$,由题意可得方程组 $\begin{cases}x+y=\frac{7}{2},\\xy=3,\end{cases}$
消去 $y$,得 $2x^{2}-7x+6=0$.
$\because \Delta =49-48=1>0$,
$\therefore x_{1}=2$,$x_{2}=\frac{3}{2}$.
$\therefore$ 满足要求的矩形 B 存在.
(1) 如果已知矩形 A 的相邻两边长分别为 2 和 1,那么请你仿照小亮的方法研究是否存在满足要求的矩形 B.
(2) 如果矩形 A 的相邻两边长分别为 $m$ 和 $n$,那么请你研究当 $m$,$n$ 满足什么条件时,矩形 B 存在,并说明理由.
当已知矩形 A 的相邻两边长分别为 6 和 1 时,小亮同学是这样研究的:
设所求矩形的相邻两边长分别是 $x$ 和 $y$,由题意可得方程组 $\begin{cases}x+y=\frac{7}{2},\\xy=3,\end{cases}$
消去 $y$,得 $2x^{2}-7x+6=0$.
$\because \Delta =49-48=1>0$,
$\therefore x_{1}=2$,$x_{2}=\frac{3}{2}$.
$\therefore$ 满足要求的矩形 B 存在.
(1) 如果已知矩形 A 的相邻两边长分别为 2 和 1,那么请你仿照小亮的方法研究是否存在满足要求的矩形 B.
(2) 如果矩形 A 的相邻两边长分别为 $m$ 和 $n$,那么请你研究当 $m$,$n$ 满足什么条件时,矩形 B 存在,并说明理由.
答案:
(1)设所求矩形的两边分别是$x$和$y$,
由题意得$\begin{cases}x + y=\frac{3}{2},\\xy = 1,\end{cases}$
消去$y$,得$2x^{2}-3x + 2 = 0$,
$\because\Delta=9 - 16<0$,
$\therefore$不存在满足要求的矩形B.
(2)当$(m + n)^{2}-8mn\geqslant0$时,矩形B存在.
理由:设所求矩形的两边长分别为$x$,$y$,
由题意得$\begin{cases}x + y=\frac{m + n}{2},\\xy=\frac{mn}{2},\end{cases}$
消去$y$,得$2x^{2}-(m + n)x + mn = 0$.
$\because\Delta=(m + n)^{2}-8mn$,
$\therefore$当$(m + n)^{2}-8mn\geqslant0$时,满足要求的矩形B存在.
(1)设所求矩形的两边分别是$x$和$y$,
由题意得$\begin{cases}x + y=\frac{3}{2},\\xy = 1,\end{cases}$
消去$y$,得$2x^{2}-3x + 2 = 0$,
$\because\Delta=9 - 16<0$,
$\therefore$不存在满足要求的矩形B.
(2)当$(m + n)^{2}-8mn\geqslant0$时,矩形B存在.
理由:设所求矩形的两边长分别为$x$,$y$,
由题意得$\begin{cases}x + y=\frac{m + n}{2},\\xy=\frac{mn}{2},\end{cases}$
消去$y$,得$2x^{2}-(m + n)x + mn = 0$.
$\because\Delta=(m + n)^{2}-8mn$,
$\therefore$当$(m + n)^{2}-8mn\geqslant0$时,满足要求的矩形B存在.
4. 请阅读下列材料,并按要求完成相应的任务:
人类对一元二次方程的研究经历了漫长的岁月. 一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中. 到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明. 我国古代三国时期的数学家赵爽也给出了类似的几何解法.
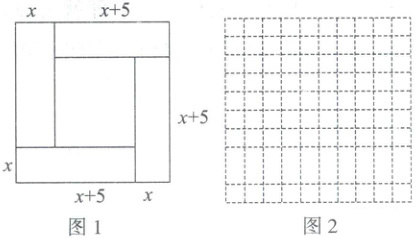
赵爽在其所著的《公股圆方图注》中记载了解方程 $x^{2}+5x-14=0$,即 $x(x+5)=14$ 的方法. 首先构造了如图 1 所示的图形,图中的大正方形面积是 $(x+x+5)^{2}$,其中四个全等的小矩形面积分别为 $x(x+5)=14$,中间的小正方形面积为 $5^{2}$,所以大正方形的面积又可表示为 $4×14+5^{2}$. 据此易得原方程的正数解为 $x=2$.
任务:
(1) 参照上述图解一元二次方程的方法,请在三个构图中选择能够说明方程 $x^{2}-3x-10=0$ 解法的正确构图是________(从序号①②③中选择).
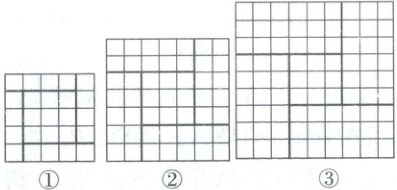
(2) 请你通过上述问题的学习,在图 2 的网格中设计正确的构图,用几何法求方程 $x^{2}+2x-15=0$ 的正数解(写出必要的思考过程)
人类对一元二次方程的研究经历了漫长的岁月. 一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中. 到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明. 我国古代三国时期的数学家赵爽也给出了类似的几何解法.
赵爽在其所著的《公股圆方图注》中记载了解方程 $x^{2}+5x-14=0$,即 $x(x+5)=14$ 的方法. 首先构造了如图 1 所示的图形,图中的大正方形面积是 $(x+x+5)^{2}$,其中四个全等的小矩形面积分别为 $x(x+5)=14$,中间的小正方形面积为 $5^{2}$,所以大正方形的面积又可表示为 $4×14+5^{2}$. 据此易得原方程的正数解为 $x=2$.

任务:
(1) 参照上述图解一元二次方程的方法,请在三个构图中选择能够说明方程 $x^{2}-3x-10=0$ 解法的正确构图是________(从序号①②③中选择).

(2) 请你通过上述问题的学习,在图 2 的网格中设计正确的构图,用几何法求方程 $x^{2}+2x-15=0$ 的正数解(写出必要的思考过程)
答案:
(1)②.
【解题过程】$\because$应构造面积是$(x + x - 3)^{2}$的大正方形,其中四个全等的小矩形面积分别为$x(x - 3)=10$,中间的小正方形面积为$3^{2}$,
$\therefore$大正方形的面积又可表示为$4×10+3^{2}=49$.
$\therefore$大正方形的边长为$7$.$\therefore x + x - 3 = 7$.
$\therefore x = 5$.
故正确构图是②.
(2)首先构造了如图所示的图形,
图中的大正方形面积是$(x + x + 2)^{2}$,其中四个全等的小矩形面积分别为$x(x + 2)=15$,中间的小正方形面积为$2^{2}$.
$\therefore$大正方形的面积又可表示为$4×15+2^{2}=64$.
进一步可知大正方形的边长为$8$,$\therefore x + x + 2 = 8$,
解得$x = 3$.

(1)②.
【解题过程】$\because$应构造面积是$(x + x - 3)^{2}$的大正方形,其中四个全等的小矩形面积分别为$x(x - 3)=10$,中间的小正方形面积为$3^{2}$,
$\therefore$大正方形的面积又可表示为$4×10+3^{2}=49$.
$\therefore$大正方形的边长为$7$.$\therefore x + x - 3 = 7$.
$\therefore x = 5$.
故正确构图是②.
(2)首先构造了如图所示的图形,
图中的大正方形面积是$(x + x + 2)^{2}$,其中四个全等的小矩形面积分别为$x(x + 2)=15$,中间的小正方形面积为$2^{2}$.
$\therefore$大正方形的面积又可表示为$4×15+2^{2}=64$.
进一步可知大正方形的边长为$8$,$\therefore x + x + 2 = 8$,
解得$x = 3$.

查看更多完整答案,请扫码查看


