第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
17. (本小题满分 8 分)计算:$(\dfrac{1}{2})^{-1} - \sqrt[3]{27} + | - 3|$.
答案:
17. 负整数指数幂 + 立方根 + 绝对值
解: 原式 = 2 - 3 + 3 = 2.
解: 原式 = 2 - 3 + 3 = 2.
18. (本小题满分 8 分)解方程组:$\begin{cases}2y - x = 7, \\ x + 3y = -2.\end{cases}$
答案:
18. 解二元一次方程组
解:$\begin{cases}2y - x = 7, ① \\x + 3y = -2. ② \end{cases}$
由① + ②得 5y = 5,
∴ y = 1(方法: 运用加减消元法先消去 x,再求出 y 的值).
将 y = 1 代入②得 x = -5.
∴ 原方程组的解为$\begin{cases} x = -5 \\ y = 1 \end{cases}$.
解:$\begin{cases}2y - x = 7, ① \\x + 3y = -2. ② \end{cases}$
由① + ②得 5y = 5,
∴ y = 1(方法: 运用加减消元法先消去 x,再求出 y 的值).
将 y = 1 代入②得 x = -5.
∴ 原方程组的解为$\begin{cases} x = -5 \\ y = 1 \end{cases}$.
19. (本小题满分 8 分)如图,在$\triangle ABC$ 中,$AB = AC = 10$,点 $D$ 在边 $BC$ 上,且 $BD = \dfrac{1}{3}BC = 4$,连接 $AD$.
(1)求 $AD$ 的长.
(2)求 $\sin\angle BAD$ 的值.
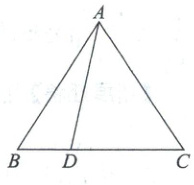
(1)求 $AD$ 的长.
(2)求 $\sin\angle BAD$ 的值.

答案:
19. 等腰三角形的性质 + 勾股定理 + 三角形的面积公式 + 锐角三角函数
解:
(1) 过点 A 作 AH⊥BC 于点 H,如图(巧作辅助线: 作垂线构造直角三角形,运用勾股定理求线段长).
∵ BD = $\frac{1}{3}$BC = 4,
∴ BC = 12.
又
∵ AB = AC = 10,
∴ BH = HC = 6.
∴ DH = 2.
在 Rt△ABH 中,AH = $\sqrt{AB² - BH²}$ = $\sqrt{10² - 6²}$ = 8.
在 Rt△ADH 中,AD = $\sqrt{AH² + DH²}$ = $\sqrt{8² + 2²}$ = 2$\sqrt{17}$.
(4分)
(2) 过点 D 作 DE⊥AB 于点 E,如图(巧作辅助线: 作三角形的高,便于求三角形的面积).
由
(1)可得 S△ABC = $\frac{1}{2}$×12×8 = 48.
∵ BD = $\frac{1}{3}$BC,
∴ S△ABD = $\frac{1}{3}$S△ABC = 16.
∴ $\frac{1}{2}$×10×DE = 16,
∴ DE = $\frac{16}{5}$.
∴ sin∠BAD = $\frac{DE}{AD}$ = $\frac{\frac{16}{5}}{2\sqrt{17}}$ = $\frac{8\sqrt{17}}{85}$.
解:
(1) 过点 A 作 AH⊥BC 于点 H,如图(巧作辅助线: 作垂线构造直角三角形,运用勾股定理求线段长).
∵ BD = $\frac{1}{3}$BC = 4,
∴ BC = 12.
又
∵ AB = AC = 10,
∴ BH = HC = 6.
∴ DH = 2.
在 Rt△ABH 中,AH = $\sqrt{AB² - BH²}$ = $\sqrt{10² - 6²}$ = 8.
在 Rt△ADH 中,AD = $\sqrt{AH² + DH²}$ = $\sqrt{8² + 2²}$ = 2$\sqrt{17}$.
(4分)
(2) 过点 D 作 DE⊥AB 于点 E,如图(巧作辅助线: 作三角形的高,便于求三角形的面积).
由
(1)可得 S△ABC = $\frac{1}{2}$×12×8 = 48.
∵ BD = $\frac{1}{3}$BC,
∴ S△ABD = $\frac{1}{3}$S△ABC = 16.
∴ $\frac{1}{2}$×10×DE = 16,
∴ DE = $\frac{16}{5}$.
∴ sin∠BAD = $\frac{DE}{AD}$ = $\frac{\frac{16}{5}}{2\sqrt{17}}$ = $\frac{8\sqrt{17}}{85}$.
查看更多完整答案,请扫码查看


