第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
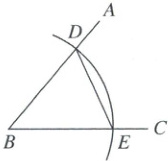
1. 如图,已知$\angle ABC = 50^{\circ}$,点$D$在$BA$上,以点$B$为圆心,$BD$长为半径画弧,交$BC$于点$E$,连接$DE$,则$\angle BDE$的度数为(
A.$50^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$115^{\circ}$
C
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$115^{\circ}$
答案:
1.C [解析] 等腰三角形的定义与性质+三角形的内角和定理 由作图可知BD = BE,即△BDE是等腰三角形,
∴∠BDE = ∠BED。
∵∠ABC = 50°,
∴∠BDE = $\frac{1}{2}$×(180°−50°) = 65°。故选C。
∴∠BDE = ∠BED。
∵∠ABC = 50°,
∴∠BDE = $\frac{1}{2}$×(180°−50°) = 65°。故选C。
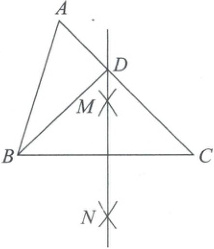
2. 如图,在$\triangle ABC$中,按以下步骤作图:①分别以点$B$和$C$为圆心,以大于$\frac{1}{2}BC$的长为半径作弧,两弧相交于点$M$和$N$;②作直线$MN$交$AC$于点$D$,连接$BD$. 若$AC = 8$,$AD = 3$,则$BD$的长为(
A.$8$
B.$5$
C.$4$
D.$3$
5
)
A.$8$
B.$5$
C.$4$
D.$3$
答案:
2.B [解析] 尺规作图+线段垂直平分线的性质
∵AC = 8,AD = 3,
∴DC = AC−AD = 8−3 = 5。由作图可知MN垂直平分线段BC,
∴BD = DC = 5。故选B。
∵AC = 8,AD = 3,
∴DC = AC−AD = 8−3 = 5。由作图可知MN垂直平分线段BC,
∴BD = DC = 5。故选B。
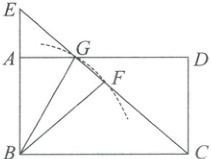
3. 如图,在矩形$ABCD$中,点$E$为$BA$延长线上一点,$F$为$CE$的中点,以$B$为圆心,$BF$长为半径的圆弧过$AD$与$CE$的交点$G$,连接$BG$. 若$AB = 4$,$CE = 10$,则$AG =$(
A.$2$
B.$2.5$
C.$3$
D.$3.5$
3
)
A.$2$
B.$2.5$
C.$3$
D.$3.5$
答案:
3.C [解析] 矩形的性质+直角三角形的性质+圆的基本概念+勾股定理 在矩形ABCD中,∠BAD = ∠ABC = 90°。
∵F是Rt△EBC斜边EC的中点,
∴BF = $\frac{1}{2}$EC = $\frac{1}{2}$×10 = 5。又点G在以B为圆心,BF长为半径的圆弧上,
∴BG = BF = 5。在Rt△ABG中,AB = 4,由勾股定理得AG = $\sqrt{BG²−AB²}$ = $\sqrt{5²−4²}$ = 3。故选C。
∵F是Rt△EBC斜边EC的中点,
∴BF = $\frac{1}{2}$EC = $\frac{1}{2}$×10 = 5。又点G在以B为圆心,BF长为半径的圆弧上,
∴BG = BF = 5。在Rt△ABG中,AB = 4,由勾股定理得AG = $\sqrt{BG²−AB²}$ = $\sqrt{5²−4²}$ = 3。故选C。
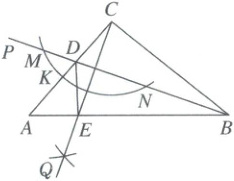
4. (2025·辽宁)如图,在$\triangle ABC$中,$AB = 16$,$BC = 12$,$CA = 10$,$\angle ABC$的平分线$BP$与$AC$相交于点$D$. 在线段$AD$上取一点$K$,以点$C$为圆心,$CK$长为半径作弧,与射线$BP$相交于点$M$和点$N$,再分别以点$M$和点$N$为圆心,大于$\frac{1}{2}MN$的长为半径作弧,两弧相交于点$Q$,作射线$CQ$,与$AB$相交于点$E$,连接$DE$. 则$\triangle DAE$的周长为( )
A.$12$
B.$14$
C.$16$
D.$18$

A.$12$
B.$14$
C.$16$
D.$18$
答案:
4.B [解析] 线段垂直平分线的性质+全等三角形的判定与性质
第1步,记BP与CQ交于点O,证明△OBC≌△OBE,得BC = BE,OC = OE
如图,记BP与CQ交于点O,由尺规作图可知BP⊥CQ,
∴∠BOC = ∠BOE = 90°。
∵BP为∠ABC的平分线,
∴∠OBC = ∠OBE。又OB = OB,
∴△OBC≌△OBE(ASA)。
∴BC = BE,OC = OE。
第2步,证明BD是线段CE的垂直平分线,得CD = DE,再利用等量代换求△DAE的周长
又
∵BD⊥CE,
∴BD是线段CE的垂直平分线。
∴CD = DE (提示:垂直平分线上的点到线段两端点的距离相等)。
∴△DAE的周长为AD + DE + AE = AD + CD + (AB−BE) = AC + AB−BC = 10 + 16−12 = 14。故选B。
4.B [解析] 线段垂直平分线的性质+全等三角形的判定与性质
第1步,记BP与CQ交于点O,证明△OBC≌△OBE,得BC = BE,OC = OE
如图,记BP与CQ交于点O,由尺规作图可知BP⊥CQ,
∴∠BOC = ∠BOE = 90°。
∵BP为∠ABC的平分线,
∴∠OBC = ∠OBE。又OB = OB,
∴△OBC≌△OBE(ASA)。
∴BC = BE,OC = OE。
第2步,证明BD是线段CE的垂直平分线,得CD = DE,再利用等量代换求△DAE的周长
又
∵BD⊥CE,
∴BD是线段CE的垂直平分线。
∴CD = DE (提示:垂直平分线上的点到线段两端点的距离相等)。
∴△DAE的周长为AD + DE + AE = AD + CD + (AB−BE) = AC + AB−BC = 10 + 16−12 = 14。故选B。

1. 用一张正方形纸板,制成一副七巧板,如图1. 在矩形区域内将它拼成一幅“火箭”图案,如图2. 若在矩形区域内随机取点,则这个点落在“火箭”图案部分的概率为(
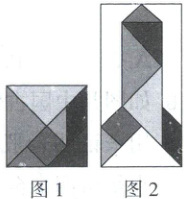
A.$\frac{1}{2}$
B.$\frac{\sqrt{2}}{2}$
C.$\frac{4}{7}$
D.$\frac{3}{8}$
A
)
A.$\frac{1}{2}$
B.$\frac{\sqrt{2}}{2}$
C.$\frac{4}{7}$
D.$\frac{3}{8}$
答案:
1.A [解析] 概率的计算 设正方形的边长为1,则七巧板的面积为1,题图2中矩形的宽为1,长为$\frac{1}{2}$+$\frac{1}{4}$+1+$\frac{1}{4}$ = 2,
∴在矩形区域内随机取点,则这个点落在“火箭”图案部分的概率为$\frac{1}{1×2}$ = $\frac{1}{2}$。故选A。
∴在矩形区域内随机取点,则这个点落在“火箭”图案部分的概率为$\frac{1}{1×2}$ = $\frac{1}{2}$。故选A。
2. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形$A$,$B$,$C$,$D$的面积分别是$3$,$5$,$2$,$3$,则最大正方形$E$的面积是(
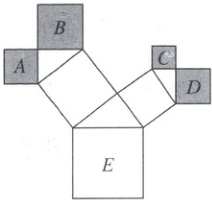
A.$8$
B.$10$
C.$13$
D.$15$
13
)
A.$8$
B.$10$
C.$13$
D.$15$
答案:
2.C [解析] 勾股定理 设中间两个正方形的边长分别为x,y,最大正方形E的边长为z,由勾股定理得,x² = 3 + 5 = 8,y² = 2 + 3 = 5,z² = x² + y² = 13,即最大正方形E的面积为13。故选C。
3. 将图1所示的七巧板拼成图2所示的四边形$ABCD$,连接$AC$,则$\tan\angle CAB$的值等于(

A.$2$
B.$\frac{1}{2}$
C.$\frac{\sqrt{5}}{5}$
D.$\frac{2\sqrt{5}}{5}$
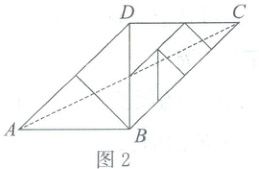
B
)
A.$2$
B.$\frac{1}{2}$
C.$\frac{\sqrt{5}}{5}$
D.$\frac{2\sqrt{5}}{5}$

答案:
3.B [解析] 锐角三角函数 设题图1中大正方形的边长为2,题图2中AC与BD交于点O,由题图可知,∠ABO = 90°,AB = BD = 2。易得四边形ABCD为平行四边形。则OB = 1。在Rt△AOB中,tan∠OAB = $\frac{OB}{AB}$ = $\frac{1}{2}$,即tan∠CAB的值等于$\frac{1}{2}$。故选B。
4. 如图源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形. 若小正方形的面积为$1$,大正方形的面积为$25$,直角三角形中较小的锐角为$\alpha$,则$\cos\alpha$的值为(
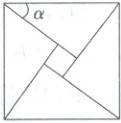
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
D
)
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
答案:
4.D [解析] 勾股定理+解方程组+余弦的定义 设直角三角形的较长直角边为a,较短直角边为b,斜边为c,
∵大正方形的面积为25,
∴c = 5。又
∵小正方形的面积为1,
∴它的边长为1。
∴a−b = 1 ①。由勾股定理得,a² + b² = 25 ②。联立①②,解得a = 4,b = 3,
∴cosα = $\frac{a}{c}$ = $\frac{4}{5}$。故选D。
∵大正方形的面积为25,
∴c = 5。又
∵小正方形的面积为1,
∴它的边长为1。
∴a−b = 1 ①。由勾股定理得,a² + b² = 25 ②。联立①②,解得a = 4,b = 3,
∴cosα = $\frac{a}{c}$ = $\frac{4}{5}$。故选D。
5. 如图,图1是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成. 若图1中大正方形的面积为$24$,小正方形的面积为$4$,现将这四个直角三角形拼成图2,则图2中大正方形的面积为(
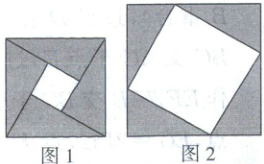
A.$24$
B.$36$
C.$40$
D.$44$
D
)
A.$24$
B.$36$
C.$40$
D.$44$
答案:
5.D [解析] 勾股定理+正方形的面积+三角形的面积公式 设直角三角形的两直角边分别为a,b(b>a),斜边为c,
∵题图1中大正方形的面积是24,
∴a² + b² = c² = 24。
∵题图1中小正方形的面积是4,
∴(b−a)² = a² + b²−2ab = 4。
∴ab = 10。
∴题图2中大正方形的面积为c² + 4×$\frac{1}{2}$ab = 24 + 2×10 = 44。故选D。
∵题图1中大正方形的面积是24,
∴a² + b² = c² = 24。
∵题图1中小正方形的面积是4,
∴(b−a)² = a² + b²−2ab = 4。
∴ab = 10。
∴题图2中大正方形的面积为c² + 4×$\frac{1}{2}$ab = 24 + 2×10 = 44。故选D。
查看更多完整答案,请扫码查看


