《2026年天利38套中考试题精选数学浙江专版》

24. （本小题满分 12 分）如图，$O$是在$\triangle ABC$内部一点，$OC$平分$\angle ACB$，以$O$为圆心，$OC$为半径的圆经过点$B$，交$AC$于点$D$，连接$BO$并延长交$\overset{\frown}{CD}$于点$E$，连接$ED$并延长交$AB$于点$F$.
（1）求证：$OC// EF$.
（2）当$\angle EBF = 2\angle A$时.
①求$\angle EFB$的度数.
②若$F$是$AB$的中点，$\odot O$的半径为 1，求$AB$的长.

答案：
24 圆周角定理的推论+三角形中位线定理+相似三角形的判定与性质+勾股定理+垂径定理+平行线的判定
解：
(1)证明：如图1，

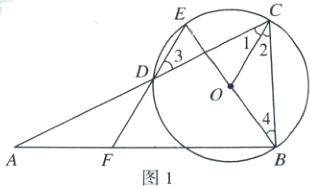
$\because OC$平分$\angle ACB$，$\therefore \angle 1 = \angle 2$.
$\because OC = OB$，
$\therefore \angle 2 = \angle 4$.
$\because \angle 4 = \angle 3$，
$\therefore \angle 1 = \angle 3$.
$\therefore OC // EF$.
(2)①由
(1)可设$\angle ADF = \angle 3 = \angle 1 = \angle 2 = x$，$\angle A = y$，
$\therefore \angle EFB = \angle A + \angle ADF = x + y$，$\angle EBF = 2\angle A = 2y$.
$\because \angle E = \angle DCB$，
$\therefore \angle E = 2x$.
在$\triangle BEF$中，$\angle E + \angle EFB + \angle EBF = 180^{\circ}$，
即$2x + (x + y) + 2y = 180^{\circ}$.
$\therefore x + y = 60^{\circ}$，即$\angle EFB = 60^{\circ}$.
②解法一（勾股定理法）：
[第1步，连接$BD$，延长$CO$交$BD$于点$R$，交$AB$于点$N$，设$DF = m$，得$NR$长]
如图2，连接$BD$，延长$CO$交$BD$于点$R$，交$AB$于点$N$（巧作辅助线：连接弦，结合圆周角定理的推论构造直角三角形，为求线段长提供条件），

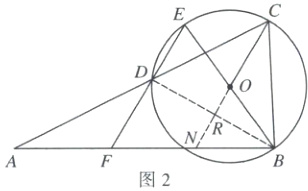
设$DF = m$.
$\because BE$是$\odot O$的直径，
$\therefore \angle BDE = 90^{\circ}$，即$BD \perp EF$.
$\because \angle EFB = 60^{\circ}$，
$\therefore BF = 2DF = 2m$，$BD = \sqrt{3}m$.
$\because OC // EF$，
$\therefore CR \perp BD$.
$\therefore DR = BR$，$CR // EF$.
$\therefore FN = BN$.
$\therefore NR = \frac{1}{2} DF = \frac{m}{2}$（提示：三角形中位线定理）.
[第2步，求$OR$，$BR$长，在$Rt \triangle BOR$中，根据勾股定理建立方程，求出$m$的值，从而可得$AB$长]
$\because F$是$AB$的中点，
$\therefore AF = \frac{2}{3} AN$.
又$EF // CN$，
$\therefore CN = \frac{3}{2} DF = \frac{3m}{2}$.
$\therefore CR = CN - NR = m$.
$\therefore OR = m - 1$.
易知$BR = \frac{\sqrt{3}m}{2}$，
在$Rt \triangle BOR$中，$OR^2 + BR^2 = OB^2$.
即$(m - 1)^2 + (\frac{\sqrt{3}m}{2})^2 = 1$，
解得$m_1 = \frac{8}{7}$，$m_2 = 0$（舍去）.
$\therefore AB = 4m = 4 × \frac{8}{7} = \frac{32}{7}$.
解法二（相似三角形法）：
[第1步，连接$BD$，作$BM // EF$，设$DF = m$，得$DM$长]
如图3，连接$BD$，过点$B$作$BM // EF$交$DC$的延长线于点$M$（巧作辅助线：作平行线，构造直角三角形，为求线段长提供条件），

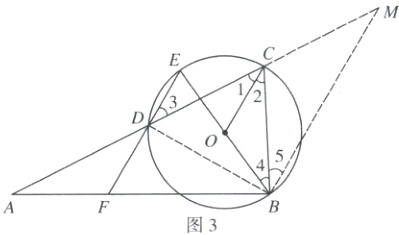
设$DF = m$，
$\because BE$是$\odot O$的直径，
$\therefore \angle BDE = 90^{\circ}$，即$BD \perp EF$.
$\because \angle EFB = 60^{\circ}$，
$\therefore BF = 2DF = 2m$，$BD = \sqrt{3}m$.
$\because BM // EF$，$F$是$AB$的中点，
$\therefore BM = 2DF = 2m$，$\angle DBM = \angle BDF = 90^{\circ}$.
$\therefore DM = \sqrt{BD^2 + BM^2} = \sqrt{(\sqrt{3}m)^2 + (2m)^2} = \sqrt{7}m$.
[第2步，求$BC$长，证明$\triangle OBC \sim \triangle CBM$，根据相似三角形的性质，求出$m$的值，从而可得$AB$长]
$\because OC // EF$，
$\therefore OC // BM$.
$\therefore \angle 1 = \angle M$，$\angle 2 = \angle 5$.
又$\because \angle 1 = \angle 2$，
$\therefore \angle M = \angle 5$.
$\therefore BC = CM = \frac{1}{2} DM = \frac{\sqrt{7}}{2}m$.
$\because \angle 2 = \angle 4 = \angle 5 = \angle M$，
$\therefore \triangle OBC \sim \triangle CBM$.
$\therefore \frac{BO}{BC} = \frac{BC}{BM}$，即$\frac{1}{\frac{\sqrt{7}}{2}m} = \frac{\frac{\sqrt{7}}{2}m}{2m}$，
解得$m_1 = \frac{8}{7}$，$m_2 = 0$（舍去）.
$\therefore AB = 4m = 4 × \frac{8}{7} = \frac{32}{7}$.
（解析人：杜伟）