《2026年天利38套中考试题精选数学浙江专版》

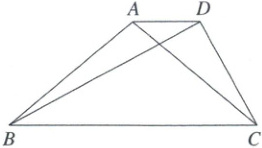
10. 如图，在$\triangle ABC$中，$AB = AC$，$\angle BAC ＞ 90^{\circ}$，$AD// BC$，$\angle BDC = 90^{\circ}$，记$AB = x$，$AD = y$，当BC不变，AB改变的过程中，下列代数式的值不变的是（C）

A.$x + y$
B.$xy$
C.$x^{2} + y^{2}$
D.$x^{2} - y^{2}$

答案： 10.C 【解析】相似三角形的判定与性质+勾股定理+矩形的判定与性质
[第1步，作$AE\perp BC$，$DF\perp BC$，证明四边形AEFD为矩形，得出$BE = CE$]
如图，作$AE\perp BC$，$DF\perp BC$（巧作辅助线：作垂线，通过构造矩形和直角三角形，将分散的线段和角度关系集中，借助图形性质建立等量关系）（规律：涉及“平行线+垂线”时，优先考虑构造矩形；涉及等腰三角形且需线段关系时，常作底边上的高），垂足分别为E，F.
∵$AD// BC$，
∴$AE\perp AD$.
∴四边形AEFD为矩形.
∵$AB = AC$，
∴$BE = CE$.
[第2步，设$BE = CE = a$为定值，表示出$BF$，$CF$，$DF^{2}$]
∵$BC$不变，
∴设$BE = CE = a$为定值.
∵$AB = x$，
∴$AE^{2}=AB^{2}-BE^{2}=x^{2}-a^{2}$.
∵四边形AEFD为矩形，
∴$AE = DF$，$EF = AD = y$.
∴$BF = a + y$，$CF = a - y$，$DF^{2}=x^{2}-a^{2}$.
[第3步，证明$\triangle BDF\sim\triangle DCF$，建立等式并化简]
∵$\angle BFD=\angle CFD=\angle BDC = 90^{\circ}$，
∴$\angle BDF=90^{\circ}-\angle CDF=\angle DCF$.
∴$\triangle BDF\sim\triangle DCF$.
∴$\frac{DF}{CF}=\frac{BF}{DF}$，
∴$DF^{2}=CF· BF$，即$x^{2}-a^{2}=(a - y)(a + y)$.
∴$x^{2}-a^{2}=a^{2}-y^{2}$，整理得$x^{2}+y^{2}=2a^{2}$.
∴$x^{2}+y^{2}$为定值.故选C.

11. 二次根式$\sqrt{x - 4}$中字母x的取值范围为$x\geqslant4$.

答案： 11. $x\geqslant4$ 【考点】二次根式有意义的条件

12. 在不透明的布袋中装有3个红球，4个白球，这些球只是颜色不同.如果布袋中再放进2个同样规格的红球，那么此时从布袋中，任意摸出一个球恰好为红球的概率是$\frac{5}{9}$.

答案： 12. $\frac{5}{9}$ 【解析】概率 由题意可得，任意摸出一个球恰好为红球的概率$\frac{3 + 2}{3 + 4 + 2}=\frac{5}{9}$.

13. 因式分解：$a^{2}b - 5ab^{2}=$$ab(a - 5b)$.

答案： 13. $ab(a - 5b)$ 【考点】因式分解

14. 如图，O为$Rt\triangle ABC$的直角边AC上一点，以OC为半径的半圆与斜边AB相切于点D，交AC于点E.已知$CE = 4$，$\angle A = 40^{\circ}$，则$\widehat{CD}$的长为__________（结果保留π）.

答案： 14. $\frac{13\pi}{9}$ 【解析】切线的性质+弧长公式 连接OD，如图.由题意可得$\angle ADO = 90^{\circ}$，$OD=\frac{1}{2}CE=\frac{1}{2}×4 = 2$，
∵$\angle A = 40^{\circ}$，
∴$\angle AOD=90^{\circ}-\angle A = 50^{\circ}$.
∴$\angle COD=180^{\circ}-\angle AOD=130^{\circ}$.
∴$l=\frac{130×\pi×2}{180}=\frac{13\pi}{9}$.

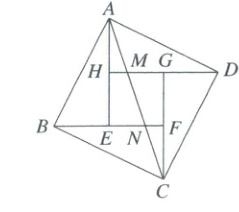
15. 如图，正方形ABCD由四个全等的直角三角形（$\triangle ABE$，$\triangle BCF$，$\triangle CDG$，$\triangle DAH$）和中间一个小正方形EFGH组成，AC与DH，BF分别交于M，N两点，若$AC = 3MN = 3$，则BN长为______________.

$\frac{\sqrt{10}}{2}$

答案： 15. $\frac{\sqrt{10}}{2}$ 【解析】全等三角形的判定与性质+勾股定理+相似三角形的判定与性质 由题意可得$AH = CF$，$\angle AHM=\angle CFN$，
∵$AE// CG$，
∴$\angle HAM=\angle FCN$.
∴$\triangle HAM\cong\triangle FCN(ASA)$.
∴$AM = CN$.
∵$AC = 3MN = MN + 2AM = 3$，
∴$AM = MN = CN = 1$，$BC=\frac{AC}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$.
∵$\angle ANE=\angle CNF$，$\angle AEN=\angle CFN$，
∴$\triangle ANE\sim\triangle CNF$.
∴$\frac{AE}{CF}=\frac{AN}{CN}=2$.设$CF = a$，则$BF = AE = 2a$.在$Rt\triangle BCF$中，$CF^{2}+BF^{2}=BC^{2}$，即$a^{2}+4a^{2}=(\frac{3\sqrt{2}}{2})^{2}$，解得$a=\frac{3\sqrt{10}}{10}$（负舍）.
∴$NF=\sqrt{CN^{2}-CF^{2}}=\frac{\sqrt{10}}{10}$.
∴$BN = BF - NF=\frac{3\sqrt{10}}{10}×2-\frac{\sqrt{10}}{10}=\frac{\sqrt{10}}{2}$.

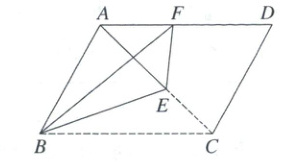
16. 如图，在平行四边形ABCD中，E为对角线AC上一点，$AE = \sqrt{2}CE$，将$\triangle BCE$沿BE折叠，点C的对应点F刚好落在AD边上，则$\triangle ABF$与平行四边形ABCD的面积之比为__________.

答案： 16. $\frac{\sqrt{2}-1}{2}$ 【解析】折叠的性质+相似三角形的判定与性质+平行四边形的性质+三角形的面积公式
[第1步，利用平行四边形及折叠的性质得出$\angle FAE=\angle EFB$]
记$AC$，$BF$相交于点$M$.
∵四边形$ABCD$是平行四边形，
∴$AD// BC$.
∴$\angle FAE=\angle ACB$.
∵将$\triangle BCE$沿$BE$折叠，点$C$的对应点$F$刚好落在$AD$边上，
∴$EF = EC$，$\angle ECB=\angle EFB$.
∴$\angle FAE=\angle EFB$.
[第2步，证明$\triangle AEF\sim\triangle FEM$，得出对应边的比例关系，再根据线段关系得出$AM = EM=\frac{1}{2}AE$]
又
∵$\angle AEF=\angle FEM$，
∴$\triangle AEF\sim\triangle FEM$.
∴$\frac{AE}{FE}=\frac{EF}{EM}$.
∵$AE=\sqrt{2}CE$，
∴$\frac{AE}{CE}=\frac{AE}{FE}=\frac{EF}{EM}=\sqrt{2}$.
∴$AE=\sqrt{2}×\sqrt{2}EM=2EM$.
∴$AM = EM=\frac{1}{2}AE$.
[第3步，设$\triangle BEM$的面积为$x$，得出$S_{\triangle ABF}$，$S_{\triangle ABC}$，进而求出$S_{□ ABCD}$，求出比值]
∵$AE=\sqrt{2}CE$，
∴$ME=\frac{\sqrt{2}}{2}CE$.设$\triangle BEM$的面积为$x$，则$S_{\triangle BEF}=S_{\triangle BEC}=\sqrt{2}x$，$S_{\triangle ABM}=x$，$S_{\triangle ABE}=2x$，
∴$S_{\triangle FME}=S_{\triangle FBE}-S_{\triangle MBE}=\sqrt{2}x - x$，即$S_{\triangle AFM}=S_{\triangle FME}=\sqrt{2}x - x$（规律：面积比常通过“等高看底、等底看高”转化为线段比，避免直接计算面积，而是利用比例关系推导）.
∴$S_{\triangle ABF}=S_{\triangle ABM}+S_{\triangle AFM}=\sqrt{2}x$，$S_{\triangle ABC}=S_{\triangle ABE}+S_{\triangle BEC}=2x+\sqrt{2}x=(2+\sqrt{2})x$.
∴$S_{□ ABCD}=2S_{\triangle ABC}=(4 + 2\sqrt{2})x$.
∴$\frac{S_{\triangle ABF}}{S_{□ ABCD}}=\frac{\sqrt{2}x}{(4 + 2\sqrt{2})x}=\frac{\sqrt{2}-1}{2}$[提示：涉及平行四边形与三角形面积比时，优先将四边形面积转化为三角形面积（通常是与对角线相关的三角形）].

17. （本小题满分8分）计算：$\sqrt{4}+\left|-\frac{1}{2}\right|-2^{-1}$.

答案： 17.实数的运算
解：原式$=-2+\frac{1}{2}-\frac{1}{2}=2$. (8分)

18. （本小题满分8分）先化简，再求值：$(\frac{1}{x - 2}+1)÷\frac{x - 1}{x^{2} - 4}$，其中$x = 3$.

答案： 18.分式的化简求值
解：原式$=\frac{x - 1}{x - 2}·\frac{(x - 2)(x + 2)}{x - 1}=x + 2$。，当$x = 3$时，原式$=5$. (8分)

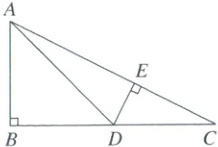
19. （本小题满分8分）如图，在$Rt\triangle ABC$中，$\angle B = 90^{\circ}$，$AB = 2$，AD是BC边上的中线，$\tan\angle BAD = 1$，$DE\perp AC$，垂足为E.
（1）求$\sin C$的值.
（2）求AE的长.

答案： 19.解直角三角形+勾股定理
解：
(1)
∵$\angle B = 90^{\circ}$，$\tan\angle BAD = 1$，
∴$BD = AB = 2$.
∵$AD$为$BC$边上的中线，
∴$BC = 2BD = 4$.
∴$AC=\sqrt{AB^{2}+BC^{2}}=2\sqrt{5}$.
∴$\sin C=\frac{AB}{AC}=\frac{\sqrt{5}}{5}$. (4分)
(2)
∵$DE\perp AC$，$\sin C=\frac{\sqrt{5}}{5}$，$CD = BD = 2$，
∴$DE = CD·\sin C=\frac{2\sqrt{5}}{5}$.
∵$BD = AB = 2$，$\angle B = 90^{\circ}$，
∴$AD=\sqrt{2}AB=2\sqrt{2}$.
∴$AE=\sqrt{AD^{2}-DE^{2}}=\frac{6\sqrt{5}}{5}$. (8分)