《2026年天利38套中考试题精选数学浙江专版》

20. （本小题满分 8 分）为了解九年级学生每周利用 DeepSeek 进行搜索、答疑、写作等科技赋能学习的情况，学校“AI 智能探究小组”成员随机调查了该校 $m$ 名九年级学生一周内的使用次数，根据统计的结果，绘制出如下两幅不完整的统计图.

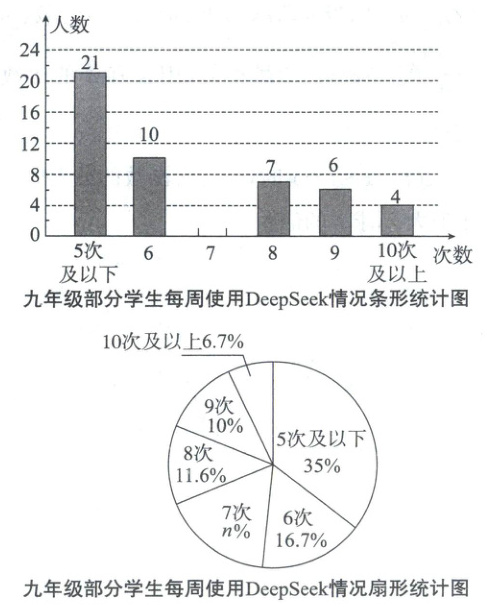
根据以上信息，解答下列问题.
（1）填空：$m =$________；$n =$________.
（2）补全条形统计图，并求所调查的这批学生每周利用 DeepSeek 进行赋能学习次数的中位数.
（3）若该校共有九年级学生 900 名，请你根据样本数据，估计该校九年级学生每周利用 DeepSeek 进行赋能学习次数达 8 次及以上的学生人数.

答案：
20. 统计图的综合应用 + 中位数 + 用样本估计总体
解:
(1) 60 20.
【解题过程】21÷35% = 60，即 m = 60.
(60 - 21 - 10 - 7 - 6 - 4)÷60×100% = 20%，即 n = 20.
(2) 补全条形统计图如图所示.
　　
将 60 名学生使用次数按从小到大的顺序排列，第 30 名和第 31 名的使用次数分别为 6，6，所以中位数为 6 次.
(3) 由题意知 900×$\frac{7 + 6 + 4}{60}$ = 255.
故估计该校九年级学生每周利用 DeepSeek 进行赋能学习次数达 8 次及以上的学生人数为 255.

21. （本小题满分 8 分）已知平行四边形 $ABCD$，在边 $AD$ 上画点 $M$，使 $CM \perp AD$ 于点 $M$. 甲、乙两位同学的作图方法如下.
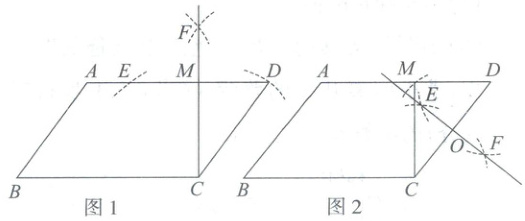
甲：如图 1，以点 $C$ 为圆心，$CD$ 长为半径画弧交边 $AD$ 于 $D$，$E$ 两点，再分别以点 $E$、点 $D$ 为圆心，大于$\dfrac{1}{2}ED$ 长为半径画弧，两弧交于点 $F$，作射线 $CF$ 交边 $AD$ 于点 $M$，则点 $M$ 为符合要求的点.
乙：如图 2，分别以点 $C$、点 $D$ 为圆心，大于$\dfrac{1}{2}CD$ 长为半径画弧，两弧交于点 $E$，$F$. 作直线 $EF$ 交边 $CD$ 于点 $O$，再以点 $O$ 为圆心，$OD$ 长为半径画弧交边 $AD$ 于点 $M$，连接 $CM$，则点 $M$ 为符合要求的点.
请判断甲、乙两位同学的作法是否正确，并选择其中一种作法说明判断理由.

答案：
21. 尺规作图 + 全等三角形的判定与性质 + 线段垂直平分线的判定与性质 + 圆周角定理的推论
解法一: 甲、乙两位同学的作法都正确.
甲同学作法正确的理由如下:
连接 CE，EF，DF，如图1.
　　　　　　
∵ CE = CD，EF = DF，CF = CF，
∴ △CEF≌△CDF(SSS).
∴ ∠ECF = ∠DCF.
又
∵ CE = CD，
∴ CF⊥DE，即点 M 为符合要求的点（提示: 运用等腰三角形的“三线合一”性质）.
解法二: 甲、乙两位同学的作法都正确.
乙同学作法正确的理由如下:
连接 CE，DE，DF，CF. 如图2.
　　　　　　
∵ CE = CF = DE = DF，
∴ EF 为线段 CD 的垂直平分线（提示: 到线段两端点距离相等的点都在这条线段的垂直平分线上）.
∴ O 为边 CD 的中点.
由作法知 CD 为⊙O 的直径，点 M 在⊙O 上，
∴ ∠CMD = 90°（提示: 直径所对的圆周角是直角）.
∴ CM⊥DA，即点 M 为符合要求的点.