《2026年天利38套中考试题精选数学浙江专版》

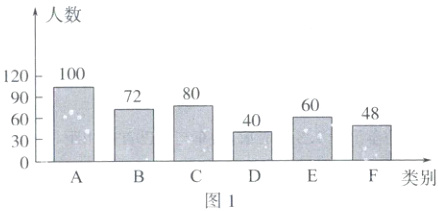
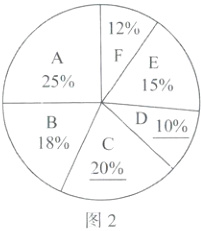
20. （本小题满分8分）近年来，研学旅行作为一种寓教于乐的教学方式多次被写入国家级政策文件.某校学生会负责该校学生的一次研学活动，为设计出同学们最感兴趣的研学路线，随机抽取了部分学生进行问卷调查，并将调查结果绘制成如下不完整的统计图（如图1，图2）.

（1）请补全条形统计图，并写出扇形统计图中C，D的百分比.
（2）“B”与“C”所在的扇形圆心角的度数和为__________°.
（3）若该校共有4 500名学生，请你估计该校对“研学+历史”最感兴趣的学生人数.

答案：
20.条形统计图+扇形统计图+用样本估计总体
解：
(1)随机抽取的学生人数为$100÷25\% = 400$，
∴$D$类别的学生人数为$400-(100 + 72 + 80 + 60 + 48)=40$.$C$类别占比为$80÷400×100\% = 20\%$.$D$类别占比为$40÷400×100\% = 10\%$.补全图形如图1,2.
　　　　
　　　　　　　　　　
(2)$136.8$. (6分)
【解题过程】$360^{\circ}×(18\% + 20\%)=136.8^{\circ}$.
(3)$4500×25\% = 1125$（人）.
∴该校对“研学+历史”最感兴趣的学生人数为1125. (8分)

21. （本小题满分8分）如图，在矩形ABCD中，$AD ＞ AB$，BD为对角线.
（1）尺规作图：作菱形BEDF，使点E，F分别在边BC，AD上.（保留作图痕迹，不写作法）
（2）在（1）的条件下，若$AB = 4$，$AD = 8$，求BE的长.

答案：
21.尺规作图+勾股定理+菱形的判定+矩形的性质
解：
(1)如图，菱形BEDF即为所求.
　　　　　　　　　　
(2)设$BE = BF = DF = x$，
∵四边形$ABCD$是矩形，
∴$\angle BAD = 90^{\circ}$，则有$BF^{2}=AB^{2}+AF^{2}$，即$x^{2}=4^{2}+(8 - x)^{2}$，解得$x = 5$.
∴$BE = 5$. (8分)

22. （本小题满分10分）某校组织学生从学校出发，乘坐大巴前往基地进行活动.大巴出发1小时后，学校因事派人乘坐轿车沿相同路线追赶.已知轿车出发2小时后追上大巴，此时两车与学校相距150千米，如图，OA，BA分别表示大巴、轿车离开学校的路程s（千米）与大巴行驶的时间t（小时）的函数图象.
（1）大巴的速度为____________千米/时.
（2）求AB所在直线的函数解析式.
（3）求轿车出发多长时间后，轿车与大巴首次相距5千米.

（1）50
（2）解：由题意得，$A(3,150)$，$B(1,0)$，设$AB$所在直线的函数解析式为$s = at + b$，把点$A(3,150)$，$B(1,0)$的坐标代入，得$\begin{cases}150 = 3a + b\\0 = a + b\end{cases}$，解得$\begin{cases}a = 75\\b = - 75\end{cases}$.
∴$AB$所在直线的函数解析式为$s = 75t - 75$.
（3）解：由（1）得大巴的速度为50千米/时.轿车的速度为$150÷(3 - 1)=75$（千米/时），设轿车出发$t$小时后，轿车与大巴首次相距5千米，由题意得，$50(t + 1)-75t = 5$，解得$t = 1.8$.答：轿车出发1.8小时后，轿车与大巴首次相距5千米.

答案： 22.一次函数的应用
解：
(1)50. (2分)
【解题过程】由题意可得，大巴的速度为$150÷3 = 50$（千米/时）.
(2)由题意得，$A(3,150)$，$B(1,0)$，设$AB$所在直线的函数解析式为$s = at + b$，把点$A(3,150)$，$B(1,0)$的坐标代入，得$\begin{cases}150 = 3a + b\\0 = a + b\end{cases}$，解得$\begin{cases}a = 75\\b = - 75\end{cases}$.
∴$AB$所在直线的函数解析式为$s = 75t - 75$. (6分)
(3)由
(1)得大巴的速度为50千米/时.轿车的速度为$150÷(3 - 1)=75$（千米/时），设轿车出发$t$小时后，轿车与大巴首次相距5千米，由题意得，$50(t + 1)-75t = 5$，解得$t = 1.8$.答：轿车出发1.8小时后，轿车与大巴首次相距5千米. (10分)