第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 下列各数:$-4,0,\sqrt{2},-\frac{1}{7}$,其中最大的数是(
A.$-4$
B.$0$
C.$\sqrt{2}$
D.$-\frac{1}{7}$
C
)A.$-4$
B.$0$
C.$\sqrt{2}$
D.$-\frac{1}{7}$
答案:
1.C [考点]实数的大小比较
2. 在平面直角坐标系中,点$P(-1,3)$在 (
A.第一象限
B.第二象限
C.第三象限
D.第四象限
B
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
2.B [考点]平面直角坐标系内点的坐标特征
3. 如图是由 6 个相同的小立方块搭成的几何体,它的左视图是 (
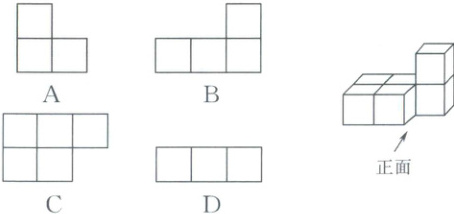
A
)
答案:
3.A [考点]三视图
4. 下列计算正确的是 ( )
A.$a^{4}+a^{4}=a^{8}$
B.$a^{4}-a^{3}=a$
C.$a^{8}÷ a^{4}=a^{2}$
D.$(-a^{3})^{2}=a^{6}$
A.$a^{4}+a^{4}=a^{8}$
B.$a^{4}-a^{3}=a$
C.$a^{8}÷ a^{4}=a^{2}$
D.$(-a^{3})^{2}=a^{6}$
答案:
4.D 解析:合并同类项+同底数幂的除法+积的乘方

故选D.
4.D 解析:合并同类项+同底数幂的除法+积的乘方

故选D.
5. 下列四组数据中方差最大的一组是 (
A.$3,3,3,3,3$
B.$2,3,3,3,4$
C.$1,2,3,4,5$
D.$0,0,3,6,6$
D
)A.$3,3,3,3,3$
B.$2,3,3,3,4$
C.$1,2,3,4,5$
D.$0,0,3,6,6$
答案:
5.D [解析]方差 对于A,平均数为3,方差$s^{2} = \frac{1}{5} × [(3 - 3)^{2} + (3 - 3)^{2} + (3 - 3)^{2} + (3 - 3)^{2} + (3 - 3)^{2}] = 0$.对于B,平均数为3,方差$s^{2} = \frac{1}{5} × [(2 - 3)^{2} + (3 - 3)^{2} + (3 - 3)^{2} + (3 - 3)^{2} + (4 - 3)^{2}] = \frac{2}{5}$.对于C,平均数为3,方差$s^{2} = \frac{1}{5} × [(1 - 3)^{2} + (2 - 3)^{2} + (3 - 3)^{2} + (4 - 3)^{2} + (5 - 3)^{2}] = 2$.对于D,平均数为3,方差$s^{2} = \frac{1}{5} × [(0 - 3)^{2} + (0 - 3)^{2} + (3 - 3)^{2} + (6 - 3)^{2} + (6 - 3)^{2}] = \frac{36}{5}$.$\because 0 < \frac{2}{5} < 2 < \frac{36}{5}$,$\therefore$方差最大的一组是D选项.故选D.
6. 若$a>b$,则下列不等式一定成立的是 ( )
A.$a-7<b-7$
B.$-3a>-3b$
C.$a+1>b-1$
D.$a^{2}>b^{2}$
A.$a-7<b-7$
B.$-3a>-3b$
C.$a+1>b-1$
D.$a^{2}>b^{2}$
答案:
6.C [解析]不等式的性质
选项 逐项分析 正误
A $\because a > b$,$\therefore a - 7 > b - 7$ ×
B $\because a > b$,$\therefore -3a < -3b$(易错:不等式的两边同时乘或除以负数,不等号的方向要改变) ×
C $\because a > b$,$a + 1 > b + 1$.$\because 1 > -1$,$\therefore b + 1 > b - 1$.$\therefore a + 1 > b - 1$. √
D 当$a > b > 0$时,$a^{2} > b^{2}$,当$a > 0 > b$且$\vert a \vert < \vert b \vert$或$b < a < 0$时,$a^{2} < b^{2}$ ×
故选C.
选项 逐项分析 正误
A $\because a > b$,$\therefore a - 7 > b - 7$ ×
B $\because a > b$,$\therefore -3a < -3b$(易错:不等式的两边同时乘或除以负数,不等号的方向要改变) ×
C $\because a > b$,$a + 1 > b + 1$.$\because 1 > -1$,$\therefore b + 1 > b - 1$.$\therefore a + 1 > b - 1$. √
D 当$a > b > 0$时,$a^{2} > b^{2}$,当$a > 0 > b$且$\vert a \vert < \vert b \vert$或$b < a < 0$时,$a^{2} < b^{2}$ ×
故选C.
7. 今有人共买物,人出八,盈三;人出七,不足四. 问人数、物价各几何. 意思是:几个人一起去买某物品,如果每人出 8 钱,则多了 3 钱;如果每人出 7 钱,则少了 4 钱. 问有多少人,物品的价格是多少.设有$x$人,则根据题意列出方程正确的是 (
A.$8x-3=7x+4$
B.$8x+3=7x-4$
C.$8x-3=7x-4$
D.$8x+3=7x+4$
A
)A.$8x-3=7x+4$
B.$8x+3=7x-4$
C.$8x-3=7x-4$
D.$8x+3=7x+4$
答案:
7.A [解析]列一元一次方程 根据“如果每人出8钱,则多了3钱”可得物品的价格为$(8x - 3)$钱,根据“如果每人出7钱,则少了4钱”可得物品的价格为$(7x + 4)$钱,$\therefore 8x - 3 = 7x + 4$.故选A.
8. 如图,在$\triangle ABC$中,以点$A$为圆心,适当长度为半径作弧,与$AB,AC$分别交于点$D,E$,分别以点$D,E$为圆心,大于$\frac{1}{2}DE$的长为半径作弧,两弧相交于点$F$,作射线$AF$交$BC$于点$G$. 以点$C$为圆心,$AC$长为半径作弧,与$AB$交于点$H$,连接$CH$,交$AG$于点$M$. 若$\angle B=34^{\circ},\angle ACB=78^{\circ}$,则$\angle AMH$的度数为 (
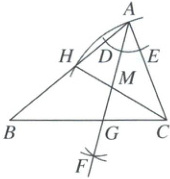
A.$88^{\circ}$
B.$78^{\circ}$
C.$68^{\circ}$
D.$58^{\circ}$
B
)
A.$88^{\circ}$
B.$78^{\circ}$
C.$68^{\circ}$
D.$58^{\circ}$
答案:
8.B [解析]尺规作图+等腰三角形的性质+三角形内角和定理 $\because \angle B = 34^{\circ}$,$\angle ACB = 78^{\circ}$,$\therefore \angle BAC = 180^{\circ} - \angle B - \angle ACB = 68^{\circ}$.根据题中尺规作图可得AF平分$\angle BAC$,$CH = CA$,$\therefore \angle BAF = \frac{1}{2} \angle BAC = 34^{\circ}$,$\angle CHA = \angle CAH = 68^{\circ}$.$\therefore \angle AMH = 180^{\circ} - \angle CHA - \angle BAF = 78^{\circ}$.故选B.
9. 已知点$A(x_{1},y_{1}),B(x_{2},y_{2}),C(x_{3},y_{3})$是反比例函数$y=\frac{k^{2}+1}{x}$($k$为常数)图象上的三点,若$x_{1}<x_{2}<x_{3}$,则下列说法正确的是 (
A.若$x_{1}x_{2}<0$,则$y_{2}<y_{3}$
B.若$x_{1}x_{2}>0$,则$y_{2}<y_{3}$
C.若$x_{2}x_{3}<0$,则$y_{1}>y_{2}$
D.若$x_{2}x_{3}>0$,则$y_{1}>y_{2}$
C
)A.若$x_{1}x_{2}<0$,则$y_{2}<y_{3}$
B.若$x_{1}x_{2}>0$,则$y_{2}<y_{3}$
C.若$x_{2}x_{3}<0$,则$y_{1}>y_{2}$
D.若$x_{2}x_{3}>0$,则$y_{1}>y_{2}$
答案:
9.C [解析]反比例函数的图象与性质 $\because k^{2} + 1 > 0$,$\therefore$反比例函数$y = \frac{k^{2} + 1}{x}$的图象位于第一、第三象限,且在每个象限内$y$随$x$的增大而减小.
选项 逐项分析 正误
A $\because x_{1} < x_{2} < x_{3}$,且$x_{1}x_{2} < 0$,$\therefore x_{1} < 0$,$x_{2} > 0$.$\therefore y_{2} > y_{3}$ ×
B $\because x_{1} < x_{2} < x_{3}$,且$x_{1}x_{2} > 0$,当$x_{1} < 0$,$x_{2} < 0$时,$x_{3}$的正负不能确定.$\therefore y_{2}$与$y_{3}$的大小不能确定 ×
C $\because x_{1} < x_{2} < x_{3}$,且$x_{2}x_{3} < 0$,$\therefore x_{2} < 0$,$x_{3} > 0$.$\therefore x_{1} < 0$.$\therefore y_{1} > y_{2}$ √
D $\because x_{1} < x_{2} < x_{3}$,且$x_{2}x_{3} > 0$,当$x_{2} > 0$,$x_{3} > 0$时,$x_{1}$的正负不能确定.$\therefore y_{1}$与$y_{2}$大小不能确定 ×
故选C.
选项 逐项分析 正误
A $\because x_{1} < x_{2} < x_{3}$,且$x_{1}x_{2} < 0$,$\therefore x_{1} < 0$,$x_{2} > 0$.$\therefore y_{2} > y_{3}$ ×
B $\because x_{1} < x_{2} < x_{3}$,且$x_{1}x_{2} > 0$,当$x_{1} < 0$,$x_{2} < 0$时,$x_{3}$的正负不能确定.$\therefore y_{2}$与$y_{3}$的大小不能确定 ×
C $\because x_{1} < x_{2} < x_{3}$,且$x_{2}x_{3} < 0$,$\therefore x_{2} < 0$,$x_{3} > 0$.$\therefore x_{1} < 0$.$\therefore y_{1} > y_{2}$ √
D $\because x_{1} < x_{2} < x_{3}$,且$x_{2}x_{3} > 0$,当$x_{2} > 0$,$x_{3} > 0$时,$x_{1}$的正负不能确定.$\therefore y_{1}$与$y_{2}$大小不能确定 ×
故选C.
10. 如图,点$E,F$是边长为 1 的正方形$ABCD$的边$AD,BC$
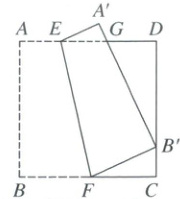
A.$\frac{y+1}{x+1}$
B.$(y+1)(x+1)$
C.$xy$
D.$x^{2}+y^{2}$
上
的
点
,将正方形沿$EF$折叠,使得点$B$的对应点$B'$在边$CD$上,$AB$的对应边$A'B'$交$AD$于点$G$,记$B'C$长为$x,AG$长为$y$,当$x,y$的值发生变化时,下列代数式的值不变的是 ( )
A.$\frac{y+1}{x+1}$
B.$(y+1)(x+1)$
C.$xy$
D.$x^{2}+y^{2}$
答案:
10.B [解析]相似三角形的判定与性质+正方形的性质+折叠的性质
[第1步,根据折叠的性质及勾股定理用含$x$的式子表示出$CF$的长]
$\because$四边形$ABCD$是正方形,且边长为1,$\therefore CD = BC = 1$,$\angle B = \angle C = \angle D = 90^{\circ}$.根据折叠的性质可得$\angle A'B'F = \angle B = 90^{\circ}$,$B'F = BF$,设$CF = m$,则$B'F = BF = 1 - m$.在$Rt \triangle B'FC$中,$CF^{2} + CB'^{2} = B'F^{2}$(技巧:折叠后点$B$的对应点$B'$在$CD$上,可利用勾股定理求出$CF$),即$m^{2} + x^{2} = (1 - m)^{2}$,解得$m = \frac{1 - x^{2}}{2}$.$\therefore CF = \frac{1 - x^{2}}{2}$.
[第2步,证明$\triangle FCB' \sim \triangle B'DG$,根据相似三角形的性质得出结果]
$\because \angle C = \angle A'B'F = 90^{\circ}$,$\therefore \angle DB'G + \angle FB'C = \angle B'FC + \angle FB'C = 90^{\circ}$.$\therefore \angle DB'G = \angle B'FC$.$\therefore \triangle FCB' \sim \triangle B'DG$(方法:根据$\angle D = \angle C = \angle A'B'F = 90^{\circ}$,可考虑“一线三等角”相似模型).$\therefore \frac{FC}{B'D} = \frac{CB'}{DG}$,即$\frac{\frac{1 - x^{2}}{2}}{1 - x} = \frac{x}{1 - y}$.整理得$xy + x + y = 1$.$\therefore (y + 1)(x + 1) = 2$为定值,故选B.
模型分析
(1)一线三等角模型(同侧型)
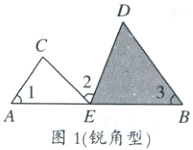
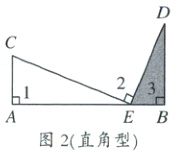
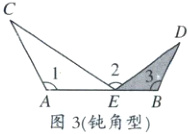
条件:如图1,2,3,$\angle 1 = \angle 2 = \angle 3$,结论:$\triangle ACE \sim \triangle BED$.
(2)一线三等角模型(异侧型)
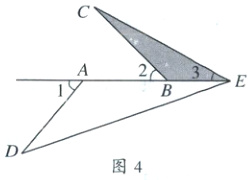
条件:如图4,$\angle 1 = \angle 2 = \angle 3$,结论:$\triangle ADE \sim \triangle BEC$.
(3)一线三等角模型(变异型)
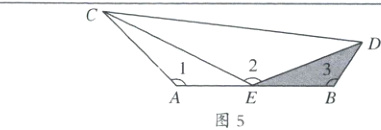
①特殊中点型.条件:如图5,若$E$为$AB$的中点,且$\angle 1 = \angle 2 = \angle 3$,结论:$\triangle ACE \sim \triangle BED \sim \triangle ECD$.
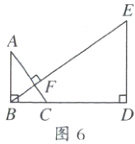
②一线三直角变异型1.条件:如图6,$\angle ABD = \angle AFE = \angle BDE = 90^{\circ}$.结论:$\triangle ABC \sim \triangle BDE \sim \triangle BFC \sim \triangle AFB$.
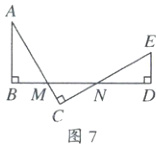
③一线三直角变异型2.条件:如图7,$\angle ABD = \angle ACE = \angle BDE = 90^{\circ}$.结论:$\triangle ABM \sim \triangle NCM \sim \triangle NDE$.
10.B [解析]相似三角形的判定与性质+正方形的性质+折叠的性质
[第1步,根据折叠的性质及勾股定理用含$x$的式子表示出$CF$的长]
$\because$四边形$ABCD$是正方形,且边长为1,$\therefore CD = BC = 1$,$\angle B = \angle C = \angle D = 90^{\circ}$.根据折叠的性质可得$\angle A'B'F = \angle B = 90^{\circ}$,$B'F = BF$,设$CF = m$,则$B'F = BF = 1 - m$.在$Rt \triangle B'FC$中,$CF^{2} + CB'^{2} = B'F^{2}$(技巧:折叠后点$B$的对应点$B'$在$CD$上,可利用勾股定理求出$CF$),即$m^{2} + x^{2} = (1 - m)^{2}$,解得$m = \frac{1 - x^{2}}{2}$.$\therefore CF = \frac{1 - x^{2}}{2}$.
[第2步,证明$\triangle FCB' \sim \triangle B'DG$,根据相似三角形的性质得出结果]
$\because \angle C = \angle A'B'F = 90^{\circ}$,$\therefore \angle DB'G + \angle FB'C = \angle B'FC + \angle FB'C = 90^{\circ}$.$\therefore \angle DB'G = \angle B'FC$.$\therefore \triangle FCB' \sim \triangle B'DG$(方法:根据$\angle D = \angle C = \angle A'B'F = 90^{\circ}$,可考虑“一线三等角”相似模型).$\therefore \frac{FC}{B'D} = \frac{CB'}{DG}$,即$\frac{\frac{1 - x^{2}}{2}}{1 - x} = \frac{x}{1 - y}$.整理得$xy + x + y = 1$.$\therefore (y + 1)(x + 1) = 2$为定值,故选B.
模型分析
(1)一线三等角模型(同侧型)



条件:如图1,2,3,$\angle 1 = \angle 2 = \angle 3$,结论:$\triangle ACE \sim \triangle BED$.
(2)一线三等角模型(异侧型)

条件:如图4,$\angle 1 = \angle 2 = \angle 3$,结论:$\triangle ADE \sim \triangle BEC$.
(3)一线三等角模型(变异型)



①特殊中点型.条件:如图5,若$E$为$AB$的中点,且$\angle 1 = \angle 2 = \angle 3$,结论:$\triangle ACE \sim \triangle BED \sim \triangle ECD$.
②一线三直角变异型1.条件:如图6,$\angle ABD = \angle AFE = \angle BDE = 90^{\circ}$.结论:$\triangle ABC \sim \triangle BDE \sim \triangle BFC \sim \triangle AFB$.
③一线三直角变异型2.条件:如图7,$\angle ABD = \angle ACE = \angle BDE = 90^{\circ}$.结论:$\triangle ABM \sim \triangle NCM \sim \triangle NDE$.
查看更多完整答案,请扫码查看


