第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
24. (本小题满分12分)综合与实践
我们已经学过,在$\triangle ABC$中,若$∠ABC=90^{\circ}$,则三角形三边满足勾股定理:$AC^{2}=AB^{2}+BC^{2}$.
【知识应用】
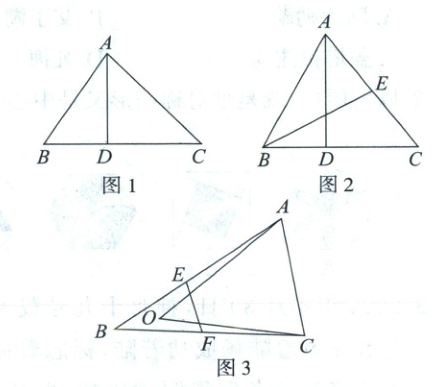
(1)如图1,在$\triangle ABC$中,$AD\perp BC$于点$D$,若$AC>AB$,则$AC^{2}-AB^{2}=BC(CD - BD)$,请说明理由.
【拓展探究】
(2)如图2,在$\triangle ABC$中,$AD\perp BC$于点$D$,点$E$是$AC$的中点,连接$BE$.求证:$BE^{2}-\frac{1}{4}AC^{2}=BD·BC$.
【拓展应用】
(3)如图3,在$\triangle ABC$中,点$E$在边$AB$上(不与点$A$,$B$重合),点$F$在边$BC$上(不与点$B$,$C$重合),连接$EF$,$∠BEF=∠BCA$,点$O$为$\triangle BEF$的外心,连接$OA$,$OC$,求证:$OC^{2}-OA^{2}=BC^{2}-BA^{2}$.
我们已经学过,在$\triangle ABC$中,若$∠ABC=90^{\circ}$,则三角形三边满足勾股定理:$AC^{2}=AB^{2}+BC^{2}$.
【知识应用】
(1)如图1,在$\triangle ABC$中,$AD\perp BC$于点$D$,若$AC>AB$,则$AC^{2}-AB^{2}=BC(CD - BD)$,请说明理由.
【拓展探究】
(2)如图2,在$\triangle ABC$中,$AD\perp BC$于点$D$,点$E$是$AC$的中点,连接$BE$.求证:$BE^{2}-\frac{1}{4}AC^{2}=BD·BC$.
【拓展应用】
(3)如图3,在$\triangle ABC$中,点$E$在边$AB$上(不与点$A$,$B$重合),点$F$在边$BC$上(不与点$B$,$C$重合),连接$EF$,$∠BEF=∠BCA$,点$O$为$\triangle BEF$的外心,连接$OA$,$OC$,求证:$OC^{2}-OA^{2}=BC^{2}-BA^{2}$.

答案:
24. 勾股定理+三角形的外心+等腰三角形的性质
解:
(1)$\because AD \perp BC$,
$\therefore \angle ADC = \angle ADB = 90°$.
$\therefore AC^2 = AD^2 + CD^2$,$AB^2 = AD^2 + BD^2$.
$\therefore AC^2 - AB^2 = AD^2 + CD^2 - AD^2 - BD^2 = CD^2 - BD^2 = (CD + BD)(CD - BD) = BC(CD - BD)$,
即$AC^2 - AB^2 = BC(CD - BD)$. (2分)
(2)证明:[第1步,作$EM \perp BC$,证明$DM = CM$]
如图,过点$E$作$EM \perp BC$于点$M$,

$\because AD \perp BC$,$\therefore AD // EM$.
$\because$点$E$是$AC$的中点,
$\therefore AE = CE$. $\therefore DM = CM$. (4分)
[第2步,运用勾股定理,得$BE^2 - \frac{1}{4}AC^2 = (BM + CM) · (BM - CM)$]
在$Rt \triangle BEM$中,由勾股定理可得$BE^2 = BM^2 + EM^2$.
在$Rt \triangle CEM$中,由勾股定理可得$CE^2 = EM^2 + CM^2$.
$\because CE = \frac{1}{2}AC$,
$\therefore \frac{1}{4}AC^2 = EM^2 + CM^2$.
$\therefore BE^2 - \frac{1}{4}AC^2 = BM^2 + EM^2 - EM^2 - CM^2 = BM^2 - CM^2 = (BM + CM)(BM - CM)$. (6分)
[第3步,等量代换,证明结论成立]
$\because BM + CM = BC$,$BM - CM = BM - DM = BD$,
$\therefore BE^2 - \frac{1}{4}AC^2 = BD · BC$. (7分)
(3)证明:[第1步,连接$OB$,$OE$,$OF$,延长$BO$交$AC$于点$N$,证明$\angle BNA = \angle BNC = 90°$,得直角三角形]
如图,连接$OB$,$OE$,$OF$,延长$BO$交$AC$于点$N$.

$\because$点$O$为$\triangle BEF$的外心,
$\therefore OB = OE = OF$(提示:三角形的外心是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等).
$\therefore \angle OBE = \angle OEB$,$\angle OBF = \angle OFB$,$\angle OEF = \angle OFE$.
$\because \angle EBF + \angle BEF + \angle BFE = 180°$,
$\therefore \angle OBE + \angle OFE + \angle OFB = \frac{1}{2} × 180° = 90°$,
即$\angle OBE + \angle BFE = 90°$.
$\because \angle BEF = \angle BCA$,$\angle BEF + \angle AEF = 180°$,
$\therefore \angle AEF + \angle BCA = 180°$.
$\because \angle BAC + \angle EFC = 180°$,
$\therefore \angle BFE = \angle BAC$.
$\therefore \angle OBE + \angle BAC = 90°$.
$\therefore \angle BNA = 90°$,
$\therefore \angle BNC = 90°$. (9分)
[第2步,运用勾股定理,代换得出结论]
在$Rt \triangle OAN$中,由勾股定理可得$OA^2 = ON^2 + AN^2$,
在$Rt \triangle OCN$中,由勾股定理可得$OC^2 = ON^2 + CN^2$,
$\therefore OC^2 - OA^2 = ON^2 + CN^2 - ON^2 - AN^2 = CN^2 - AN^2$.
在$Rt \triangle ABN$中,由勾股定理可得$BA^2 = BN^2 + AN^2$,
在$Rt \triangle BCN$中,由勾股定理可得$BC^2 = BN^2 + CN^2$,
$\therefore BC^2 - BA^2 = BN^2 + CN^2 - BN^2 - AN^2 = CN^2 - AN^2$.
$\therefore OC^2 - OA^2 = BC^2 - BA^2$. (12分)
(解析人:宋 旭)
24. 勾股定理+三角形的外心+等腰三角形的性质
解:
(1)$\because AD \perp BC$,
$\therefore \angle ADC = \angle ADB = 90°$.
$\therefore AC^2 = AD^2 + CD^2$,$AB^2 = AD^2 + BD^2$.
$\therefore AC^2 - AB^2 = AD^2 + CD^2 - AD^2 - BD^2 = CD^2 - BD^2 = (CD + BD)(CD - BD) = BC(CD - BD)$,
即$AC^2 - AB^2 = BC(CD - BD)$. (2分)
(2)证明:[第1步,作$EM \perp BC$,证明$DM = CM$]
如图,过点$E$作$EM \perp BC$于点$M$,

$\because AD \perp BC$,$\therefore AD // EM$.
$\because$点$E$是$AC$的中点,
$\therefore AE = CE$. $\therefore DM = CM$. (4分)
[第2步,运用勾股定理,得$BE^2 - \frac{1}{4}AC^2 = (BM + CM) · (BM - CM)$]
在$Rt \triangle BEM$中,由勾股定理可得$BE^2 = BM^2 + EM^2$.
在$Rt \triangle CEM$中,由勾股定理可得$CE^2 = EM^2 + CM^2$.
$\because CE = \frac{1}{2}AC$,
$\therefore \frac{1}{4}AC^2 = EM^2 + CM^2$.
$\therefore BE^2 - \frac{1}{4}AC^2 = BM^2 + EM^2 - EM^2 - CM^2 = BM^2 - CM^2 = (BM + CM)(BM - CM)$. (6分)
[第3步,等量代换,证明结论成立]
$\because BM + CM = BC$,$BM - CM = BM - DM = BD$,
$\therefore BE^2 - \frac{1}{4}AC^2 = BD · BC$. (7分)
(3)证明:[第1步,连接$OB$,$OE$,$OF$,延长$BO$交$AC$于点$N$,证明$\angle BNA = \angle BNC = 90°$,得直角三角形]
如图,连接$OB$,$OE$,$OF$,延长$BO$交$AC$于点$N$.

$\because$点$O$为$\triangle BEF$的外心,
$\therefore OB = OE = OF$(提示:三角形的外心是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等).
$\therefore \angle OBE = \angle OEB$,$\angle OBF = \angle OFB$,$\angle OEF = \angle OFE$.
$\because \angle EBF + \angle BEF + \angle BFE = 180°$,
$\therefore \angle OBE + \angle OFE + \angle OFB = \frac{1}{2} × 180° = 90°$,
即$\angle OBE + \angle BFE = 90°$.
$\because \angle BEF = \angle BCA$,$\angle BEF + \angle AEF = 180°$,
$\therefore \angle AEF + \angle BCA = 180°$.
$\because \angle BAC + \angle EFC = 180°$,
$\therefore \angle BFE = \angle BAC$.
$\therefore \angle OBE + \angle BAC = 90°$.
$\therefore \angle BNA = 90°$,
$\therefore \angle BNC = 90°$. (9分)
[第2步,运用勾股定理,代换得出结论]
在$Rt \triangle OAN$中,由勾股定理可得$OA^2 = ON^2 + AN^2$,
在$Rt \triangle OCN$中,由勾股定理可得$OC^2 = ON^2 + CN^2$,
$\therefore OC^2 - OA^2 = ON^2 + CN^2 - ON^2 - AN^2 = CN^2 - AN^2$.
在$Rt \triangle ABN$中,由勾股定理可得$BA^2 = BN^2 + AN^2$,
在$Rt \triangle BCN$中,由勾股定理可得$BC^2 = BN^2 + CN^2$,
$\therefore BC^2 - BA^2 = BN^2 + CN^2 - BN^2 - AN^2 = CN^2 - AN^2$.
$\therefore OC^2 - OA^2 = BC^2 - BA^2$. (12分)
(解析人:宋 旭)
查看更多完整答案,请扫码查看


