第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. $\frac{3}{4}$的相反数是(
A.$-\frac{3}{4}$
B.$\frac{3}{4}$
C.$-\frac{4}{3}$
D.$\frac{4}{3}$
A
)A.$-\frac{3}{4}$
B.$\frac{3}{4}$
C.$-\frac{4}{3}$
D.$\frac{4}{3}$
答案:
1.A [考点]相反数
2. 如图所示,直线$a$,$b$被直线$c$所截.若$a// b$,$\angle 1 = 91^{\circ}$,则(
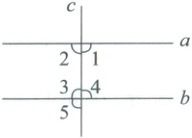
A.$\angle 2 = 91^{\circ}$
B.$\angle 3 = 91^{\circ}$
C.$\angle 4 = 91^{\circ}$
D.$\angle 5 = 91^{\circ}$
B
)
A.$\angle 2 = 91^{\circ}$
B.$\angle 3 = 91^{\circ}$
C.$\angle 4 = 91^{\circ}$
D.$\angle 5 = 91^{\circ}$
答案:
2.B [解析]平行线的性质
∵a//b,
∴∠3=∠1=91°,∠2=∠4=∠5=180°−∠3=89°.故选B.
∵a//b,
∴∠3=∠1=91°,∠2=∠4=∠5=180°−∠3=89°.故选B.
3. 国家税务总局发布的数据显示,2024年,现行支持科技创新和制造业发展的主要政策减税降费及退税达26 293亿元,助力我国新质生产力加速培育、制造业高质量发展.将数2 629 300 000 000用科学记数法表示为(
A.$26.293× 10^{11}$
B.$2.6293× 10^{12}$
C.$0.26293× 10^{13}$
D.$2.6293× 10^{13}$
B
)A.$26.293× 10^{11}$
B.$2.6293× 10^{12}$
C.$0.26293× 10^{13}$
D.$2.6293× 10^{13}$
答案:
3.B [考点]科学记数法
4. 底面是正六边形的直棱柱如图所示,其俯视图是(
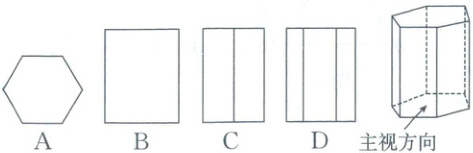
A
)
答案:
4.A [解析]三视图 从几何体的上面往下看得到的几何图形如选项A中图形所示,故选A.
5. 已知反比例函数$y = \frac{-7}{x}$.下列选项正确的是(
A.函数图象在第一、三象限
B.$y$随$x$的增大而减小
C.函数图象在第二、四象限
D.$y$随$x$的增大而增大
C
)A.函数图象在第一、三象限
B.$y$随$x$的增大而减小
C.函数图象在第二、四象限
D.$y$随$x$的增大而增大
答案:
5.C [解析]反比例函数的图象与性质 在反比例函数y=$\frac{−7}{x}$中,−7<0,
∴函数图象位于第二、四象限,且在每个象限内y随x的增大而增大.故选C.
∴函数图象位于第二、四象限,且在每个象限内y随x的增大而增大.故选C.
6. 如图,五边形$ABCDE$,$A'B'C'D'E'$是以坐标原点$O$为位似中心的位似图形,已知点$A$,$A'$的坐标分别为$(2,0)$,$(3,0)$.若$DE$的长为3,则$D'E'$的长为(
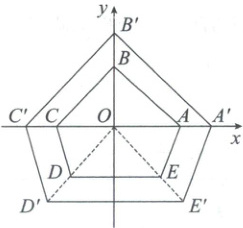
A.$\frac{7}{2}$
B.4
C.$\frac{9}{2}$
D.5
C
)
A.$\frac{7}{2}$
B.4
C.$\frac{9}{2}$
D.5
答案:
6.C [解析]位似图形的性质+相似三角形的判定与性质 由题知,$\frac{OE}{O'E'}$=$\frac{OD}{O'D'}$=$\frac{OA}{OA'}$=$\frac{2}{3}$,∠DOE=∠D'OE',
∴△DOE∽△D'OE'(关键:位似图形的对应顶点与位似中心连线所得图形是相似图形).
∴$\frac{DE}{D'E'}$=$\frac{OE}{O'E'}$=$\frac{2}{3}$.
∵DE=3,
∴D'E'=$\frac{9}{2}$.故选C.
∴△DOE∽△D'OE'(关键:位似图形的对应顶点与位似中心连线所得图形是相似图形).
∴$\frac{DE}{D'E'}$=$\frac{OE}{O'E'}$=$\frac{2}{3}$.
∵DE=3,
∴D'E'=$\frac{9}{2}$.故选C.
7. 手工社团的同学制作两种手工艺品$A$和$B$,需要用到彩色纸和细木条,单个手工艺品材料用量如下表.

如果一共用了17张彩色纸和10捆细木条,问他们制作的两种手工艺品各有多少个?设手工艺品$A$有$x$个,手工艺品$B$有$y$个,则$x$和$y$满足的方程组是(
A.$\begin{cases}5x + 3y = 17,\\2x + y = 10\end{cases}$
B.$\begin{cases}5x + 3y = 10,\\2x + y = 17\end{cases}$
C.$\begin{cases}5x + 2y = 17,\\3x + y = 10\end{cases}$
D.$\begin{cases}5x + 2y = 10,\\3x + y = 17\end{cases}$

如果一共用了17张彩色纸和10捆细木条,问他们制作的两种手工艺品各有多少个?设手工艺品$A$有$x$个,手工艺品$B$有$y$个,则$x$和$y$满足的方程组是(
C
)A.$\begin{cases}5x + 3y = 17,\\2x + y = 10\end{cases}$
B.$\begin{cases}5x + 3y = 10,\\2x + y = 17\end{cases}$
C.$\begin{cases}5x + 2y = 17,\\3x + y = 10\end{cases}$
D.$\begin{cases}5x + 2y = 10,\\3x + y = 17\end{cases}$
答案:
7.C [考点]二元一次方程组的应用
23. (本小题满分10分)在直角坐标系中,设函数$y=(x - m)(x - m - 2)$($m$是常数).
(1)当$m=5$时,求该函数图象与$x$轴的交点坐标.
(2)若点$A(n,y_{1})$,$B(m + 1,y_{2})$,$C(x_{0},3)$都在该函数图象上,点$A$不与点$B$,$C$重合.
①比较$y_{1}$,$y_{2}$的大小.
②若$x_{0}=-1$,$y_{1}>3$,直接写出$n$的取值范围.
(1)当$m=5$时,求该函数图象与$x$轴的交点坐标.
(2)若点$A(n,y_{1})$,$B(m + 1,y_{2})$,$C(x_{0},3)$都在该函数图象上,点$A$不与点$B$,$C$重合.
①比较$y_{1}$,$y_{2}$的大小.
②若$x_{0}=-1$,$y_{1}>3$,直接写出$n$的取值范围.
答案:
23. 二次函数的图象与性质
解:
(1)当$m = 5$时,$y = (x - 5)(x - 7)$,令$y = 0$,
则$(x - 5)(x - 7) = 0$,解得$x = 5$或$x = 7$,
$\therefore$该函数图象与$x$轴的交点坐标为$(5, 0)$,$(7, 0)$. (2分)
(2)①解法一(求值法):将点$B(m + 1, y_2)$的坐标代入函数表达式,得
$y_2 = (m + 1 - m)(m + 1 - m - 2) = 1 × (-1) = -1$;
将点$A(n, y_1)$的坐标代入函数表达式,得
$y_1 = (n - m)(n - m - 2)$. (4分)
若令$k = n - m$,则$y_1 = k(k - 2) = k^2 - 2k$.
该函数图象开口向上,顶点坐标为$(1, -1)$,
当$k = 1$时,$n = m + 1$,此时$A$,$B$重合,不符合题意,
$\therefore y_1 > -1$.
$\therefore y_1 > y_2$. (6分)
解法二(图象法):$\because y = (x - m)(x - m - 2) = x^2 - (2m + 2)x + m(m + 2)$,
$\therefore$对称轴为直线$x = -\frac{-(2m + 2)}{2} = m + 1$.
$\therefore$点$B$是抛物线的顶点. (4分)
$\because$抛物线开口向上,
$\therefore y_2$最小.$\therefore y_1 > y_2$. (6分)
②当$m = 0$时,$n > 3$或$n < -1$;
当$m = -4$时,$n > -1$或$n < -5$. (10分)
【解题过程】当$x_0 = -1$时,点$C$的坐标为$(-1, 3)$,代入得$(-1 - m)(-1 - m - 2) = 3$,解得$m = 0$或$m = -4$.
当$m = 0$时,$y = x(x - 2) = x^2 - 2x$,
$\because y_1 > 3$,
$\therefore n^2 - 2n > 3$,
即$(n - 3)(n + 1) > 0$,解得$n > 3$或$n < -1$.
当$m = -4$时,$y = (x + 4)(x + 2) = x^2 + 6x + 8$,
$\because y_1 > 3$,
$\therefore n^2 + 6n + 8 > 3$,即$(n + 1)(n + 5) > 0$,
解得$n > -1$或$n < -5$.
综上所述,当$m = 0$时,$n > 3$或$n < -1$;当$m = -4$时,$n > -1$或$n < -5$.
解:
(1)当$m = 5$时,$y = (x - 5)(x - 7)$,令$y = 0$,
则$(x - 5)(x - 7) = 0$,解得$x = 5$或$x = 7$,
$\therefore$该函数图象与$x$轴的交点坐标为$(5, 0)$,$(7, 0)$. (2分)
(2)①解法一(求值法):将点$B(m + 1, y_2)$的坐标代入函数表达式,得
$y_2 = (m + 1 - m)(m + 1 - m - 2) = 1 × (-1) = -1$;
将点$A(n, y_1)$的坐标代入函数表达式,得
$y_1 = (n - m)(n - m - 2)$. (4分)
若令$k = n - m$,则$y_1 = k(k - 2) = k^2 - 2k$.
该函数图象开口向上,顶点坐标为$(1, -1)$,
当$k = 1$时,$n = m + 1$,此时$A$,$B$重合,不符合题意,
$\therefore y_1 > -1$.
$\therefore y_1 > y_2$. (6分)
解法二(图象法):$\because y = (x - m)(x - m - 2) = x^2 - (2m + 2)x + m(m + 2)$,
$\therefore$对称轴为直线$x = -\frac{-(2m + 2)}{2} = m + 1$.
$\therefore$点$B$是抛物线的顶点. (4分)
$\because$抛物线开口向上,
$\therefore y_2$最小.$\therefore y_1 > y_2$. (6分)
②当$m = 0$时,$n > 3$或$n < -1$;
当$m = -4$时,$n > -1$或$n < -5$. (10分)
【解题过程】当$x_0 = -1$时,点$C$的坐标为$(-1, 3)$,代入得$(-1 - m)(-1 - m - 2) = 3$,解得$m = 0$或$m = -4$.
当$m = 0$时,$y = x(x - 2) = x^2 - 2x$,
$\because y_1 > 3$,
$\therefore n^2 - 2n > 3$,
即$(n - 3)(n + 1) > 0$,解得$n > 3$或$n < -1$.
当$m = -4$时,$y = (x + 4)(x + 2) = x^2 + 6x + 8$,
$\because y_1 > 3$,
$\therefore n^2 + 6n + 8 > 3$,即$(n + 1)(n + 5) > 0$,
解得$n > -1$或$n < -5$.
综上所述,当$m = 0$时,$n > 3$或$n < -1$;当$m = -4$时,$n > -1$或$n < -5$.
查看更多完整答案,请扫码查看


