《2026年天利38套中考试题精选数学浙江专版》

9. 已知$P(t,y_{1})$，$Q(t + 4,y_{2})$两点在反比例函数$y=\frac{4}{x}$的图象上.下列判断正确的是（A）
A.当$t ＜ -4$时，$y_{2} ＜ y_{1} ＜ 0$
B.当$-4 ＜ t ＜ 0$时，$y_{2} ＜ y_{1} ＜ 0$
C.当$-4 ＜ t ＜ 0$时，$0 ＜ y_{1} ＜ y_{2}$
D.当$t ＞ 0$时，$0 ＜ y_{1} ＜ y_{2}$

答案： 9.A 【解析】反比例函数的图象与性质 反比例函数$y = \frac{4}{x}$图象的两个分支分别位于第一、三象限,在每一个象限内,$y$随$x$的增大而减小.对于A,当$t ＜ -4$时,$t + 4 ＜ 0$,$\therefore$点$P(t,y_{1})$,$Q(t + 4,y_{2})$在第三象限.$\because t ＜ t + 4$,$\therefore y_{2} ＜ y_{1} ＜ 0$.故A正确.
对于B,C,当$-4 ＜ t ＜ 0$时,点$P(t,y_{1})$在第三象限,点$Q(t + 4,y_{2})$在第一象限,$\therefore y_{1} ＜ 0$,$y_{2} ＞ 0$.$\therefore y_{1} ＜ 0 ＜ y_{2}$.故B,C错误.对于D,当$t ＞ 0$时,$t + 4 ＞ 0$,$\therefore P(t,y_{1})$,$Q(t + 4,y_{2})$在第一象限.$\because t ＜ t + 4$,$\therefore y_{1} ＞ y_{2} ＞ 0$.故D错误.故选A.

10. 如图，在$□ ABCD$中，对角线$AC$，$BD$相交于点$O$，$AC = 2$，$BD = 2\sqrt{3}$.过点$A$作$BC$的垂线交$BC$于点$E$，记$BE$长为$x$，$BC$长为$y$.当$x$，$y$的值变化时，下列代数式的值不变的是（ ）


A.$x + y$
B.$x - y$
C.$xy$
D.$x^{2}+y^{2}$

答案：
10.C 【解析】平行四边形的性质+全等三角形的判定与性质+勾股定理
【思维导图】已知条件$\to$过点$D$作$DH \perp BC$,交$BC$的延长线于点$H$
平行四边形的性质$\to CH = BE = x \to EC$,$BH \to$勾股定理$\to xy = 2$.
如图,过点$D$作$DH \perp BC$,交$BC$的延长线于点$H$,在平行四边形$ABCD$中,$AB = DC$,$AD // BC$.$\because AE \perp BC$,$DH \perp BC$,$\therefore AE = DH$.$\therefore Rt \triangle DCH \cong Rt \triangle ABE(HL)$.$\therefore CH = BE = x$.
$\because BC = y$,$\therefore EC = BC - BE = y - x$,$BH = BC + CH = y + x$.
$\because AE^{2} = AC^{2} - EC^{2}$,$DH^{2} = BD^{2} - BH^{2}$,$\therefore 2^{2} - (y - x)^{2} = 12 - (y + x)^{2}$.$\therefore xy = 2$.故选C.

11. 分解因式：$a^{2}-7a=$$a(a - 7)$.

答案： 11.$a(a - 7)$

12. 若$\frac{2}{x - 1}=1$，则$x=$3.

答案： 12.3 【解析】解分式方程 由题知,$2 = x - 1$,$x = 3$.

13. 如图，$AB$是$\odot O$的直径，$AC$是$\odot O$的切线，$A$为切点，连接$BC$.已知$\angle ACB = 50^{\circ}$，则$\angle B$的度数为__________.

40°

答案： 40°

【解析】切线的性质 由题知,BA⊥AC,
∴∠BAC=90∘.

∵∠ACB=50∘,
∴∠B=90∘−50∘=40∘.

14. 有8张卡片，上面分别写着数1，2，3，4，5，6，7，8.从中随机抽取1张卡片，该卡片上的数是4的整数倍的概率是$\frac{1}{4}$.

答案： 14 $\frac{1}{4}$ 【解析】随机事件的概率 由题知,共8张卡片,且卡片上的数是4的整数倍的数是4,8,有2张卡片,故所求概率为$\frac{2}{8} = \frac{1}{4}$.

15. 如图，$D$，$E$分别是$\triangle ABC$边$AB$，$AC$的中点，连接$BE$，$DE$.若$\angle AED=\angle BEC$，$DE = 2$，则$BE$的长为__________.

4

答案： 15.4 【解析】三角形中位线定理+等腰三角形的判定 $\because D$,$E$分别是$\triangle ABC$边$AB$,$AC$的中点,$\therefore BC = 2DE = 2 × 2 = 4$,$DE // BC$.$\therefore \angle AED = \angle C$.$\because \angle AED = \angle BEC$,$\therefore \angle BEC = \angle C$.$\therefore BE = BC = 4$(提示:等角对等边).

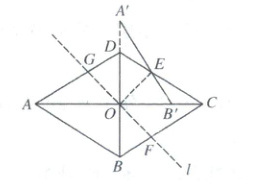
16. 如图，在菱形$ABCD$中，对角线$AC$，$BD$相交于点$O$，$\frac{AC}{BD}=\frac{5}{3}$.线段$AB$与$A'B'$关于过点$O$的直线$l$对称，点$B$的对应点$B'$在线段$OC$上，$A'B'$交$CD$于点$E$，则$\triangle B'CE$与四边形$OB'ED$的面积比为__________.

答案：
1:3 【解析】菱形的性质+轴对称的性质+全等三角形的判定与性质
∵ 四边形 $ABCD$ 是菱形，且 $\frac{AC}{BD}=\frac{5}{3}$，
∴ 设 $AC = 10k$，则 $BD = 6k$。
∴ $OA = OC = 5k$，$OB = OD = 3k$。如图，连接 $A'D$，$OE$，记直线 $l$ 分别交 $BC$，$AD$ 于点 $F$，$G$，
∵ 线段 $AB$ 与 $A'B'$ 关于过点 $O$ 的直线 $l$ 对称，点 $B$ 的对称点 $B'$ 在线段 $OC$ 上，
∴ $\angle BOF=\angle COF=\frac{1}{2}\angle BOB' = 45^{\circ}$，$OA' = OA = 5k$，$OB' = OB = 3k$。
∴ $\angle AOG=\angle DOG = 45^{\circ}$（提示：$AC\perp BD$）。
∴ $A'$，$D$，$O$ 三点共线。
∴ $A'D = B'C = 2k$。
∵ $AB// CD$，
∴ $\angle CDO=\angle ABO$。由对称性可得 $\angle A'B'O=\angle ABO$，
∴ $\angle A'B'O=\angle CDO$。
∴ $\angle A'DE=\angle CB'E$。又 $\angle A'ED=\angle CEB'$，
∴ $\triangle A'ED\cong\triangle CEB'(AAS)$。
∴ $CE = A'E$。
∵ $AB = A'B' = CD$，
∴ $DE = B'E$。又 $OE = OE$，$OD = OB'$，
∴ $\triangle DOE\cong\triangle B'OE(SSS)$。
∴ $S_{\triangle DOE}=S_{\triangle B'OE}$。
∵ $\frac{S_{\triangle B'CE}}{S_{\triangle B'OE}}=\frac{B'C}{B'O}=\frac{2}{3}$，
∴ $\frac{S_{\triangle B'CE}}{S_{四边形OB'ED}}=\frac{2}{6}=\frac{1}{3}$。

17. （本小题满分8分）计算：$(\frac{1}{4})^{-1}-\sqrt[3]{8}+\vert - 5\vert$.

答案： 17.实数的运算
解:$(\frac{1}{4})^{-1} - \sqrt[3]{8} + | - 5| = 4 - 2 + 5 = 7$.(8分)

18. （本小题满分8分）解方程组：$\begin{cases}2x - y = 5,\\4x + 3y = -10.\end{cases}$

答案： 18.解二元一次方程组
解:标记方程组:$\begin{cases}2x - y = 5, ① \\4x + 3y = -10. ② \end{cases}$
由①$× 3 +$②,得$10x = 5$,
解得$x = \frac{1}{2}$. (4分)
把$x = \frac{1}{2}$代入①,得$y = -4$. (6分)
所以原方程组的解为$\begin{cases} x = \frac{1}{2}, \\ y = -4. \end{cases}$ (8分)

19. （本小题满分8分）如图，在$\triangle ABC$中，$AD\perp BC$，垂足为$D$，$AE$是边$BC$上的中线，$AB = 10$，$AD = 6$，$\tan\angle ACB = 1$.
(1)求$BC$的长.
(2)求$\sin\angle DAE$的值.

答案： 19.锐角三角函数+勾股定理
解:
(1)因为$AD \perp BC$,$AB = 10$,$AD = 6$,
所以$BD = \sqrt{AB^{2} - AD^{2}} = \sqrt{10^{2} - 6^{2}} = 8$. (2分)
因为$\tan \angle ACB = \frac{AD}{CD} = 1$,所以$CD = 6$.
故$BC = 14$. (4分)
(2)因为$AE$是边$BC$上的中线,
所以$BE = CE = 7$.
进而$DE = 1$. (6分)
所以$AE = \sqrt{37}$.
因此$\sin \angle DAE = \frac{1}{\sqrt{37}} = \frac{\sqrt{37}}{37}$. (8分)